Переменных
Определение. Если каждой паре (x,y) значений двух независимых переменных из области Wставится определенное значение z, то говорят, что z есть функция двух переменных (x,y).
z=f(x,y)
Геометрическое изображение функции двух переменных - поверхность.
Частное и полное приращение функции.
Полное приращение функции
|
Частное приращение функции
|
|
Вообще, полное приращение функции не равно сумме частных приращений.
Пример. z=xy.
|
|
|
Непрерывность функции нескольких переменных
Предел функции.
Пусть z=f(x,y) определена в некоторой окрестности A(x0,y0).
Определение. Постоянное число b называют пределом z=f(x,y) при P(x,y) стремящемся к A, если для любого e > 0 можно указать такое значение d > 0, что для всех x, удовлетворяющих неравенству |AP| < d, имеет место неравенство |f(x,y)-b| < e.
Непрерывная функция
Частные производные
Предел функции
Предел функции. Число L называется пределом функции y = f ( x ) при x, стремящемся к a :
если
для любого 
> 0 найдётся
такое положительное число 
= 
( 
), зависящее
от 
, что из
условия | x - a | < 
следует
| f ( x )
– L |
< 
.
Это
определение означает,
что L есть предел функции y = f ( x ),
если значение функции неограниченно
приближается к L ,
когда значение аргумента x приближается
к a.
Геометрически это значит, что для
любого 
> 0
можно найти такое число
,
что еслиx
находится в интервале ( a - 
,a + 
),
то значение функции лежит в интервале
(L - 
,L + 
).
Отметим, что в соответствии с этим
определением аргумент функции
лишьприближается
к a ,
не принимая этого значения! Это следует
учитывать при вычислении предела любой
функции в точке её разрыва, где
функция не существует.
Непрерывность функции двух переменных
Пусть функция z = f ( x ,y ) определена в точке M0(x0y0) и её окрестности.
Определение 1.6 Функция называется непрерывной в точке M0(x0y0), если
Если функция f ( x ,y ) непрерывна в точке M0(x0y0), то
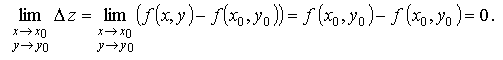
Поскольку
То есть, если функция f ( x ,y ) непрерывна в точке M0(x0y0), то бесконечно малым приращениям аргументов в этой области соответствует бесконечно малое приращениеΔzфункции z.
Справедливо и обратное утверждение: если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции, то функция непрерывна
Функцию, непрерывную в каждой точке области, называют непрерывной в области. Для непрерывных функций двух переменных, так же, как и для функции одной переменной, непрерывной на отрезке, справедливы основополагающие теоремы Вейерштрасса и Больцано - Коши.
Свойства функций, непрерывных в ограниченной замкнутой области координатах
Свойства функций, непрерывных в ограниченной замкнутой области
Приведем свойства функций, непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной — см. п. 19.5). Предварительно уточним понятие области.
Областью называется множество точек плоскости, обладающих свойствами открытости и связности.
Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.
Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.
Точка No называется граничной точкой области D, если она не принадлежит D, но в любой окрестности ее лежат точки этой области. Совокупность граничных точек области D называется границей D. Область D с присоединенной к ней границей называется замкнутой областью, обозначается D. Область называется ограниченной, если все ее точки принадлежат неко торому кругу радиуса R. В противном случае область называется неограниченной. Примером неограниченной области может служить множество точек первого координатного угла, а примером ограниченной — (d-окрестность точки М0(х0;у0).
Теорема 43.1. Если функция z = f(N) непрерывна в ограниченной замкнутой области, то она в этой области: а) ограничена, т. е. существует такое число R > О, что для всех точек N в этой области выполняется неравенство |f(N)| < R; б) имеет точки, в которых принимает наименьшее т и наибольшее М значения; в) принимает хотя бы в одной точке области любое численное значение, заключенное между m и М.
Теорема дается без доказательства.
28-частные производные первого порядка и их геометрический смысл
Частные
производные первого порядка. Пусть
функция 
определена
в области 
и 
.
Тогда при малых 
определено
ее частное приращение по 
: 
.
Определение. Частной
производной функции 
по
переменной 
в
точке 
называют
предел
,
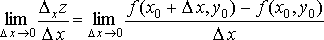если он существует.
Частную
производную по 
обозначают
одним из следующих символов:
.
Аналогично
определяется частная производная
по 
и
вводятся ее обозначения.
Легко видеть, что частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной.
Пример.
Найти частные производные функции 
.
Имеем:
, 
.
29-Частные производные высших порядков Теорема Шварц
Частные
производные высших порядков. Рассматривая
частные производные 
и 
как
функции от 
,
приходим к понятиям частных производных
второго порядка. А именно, выражения
, 
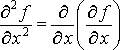называют частными
производными второго порядка функции 
по 
и
по 
соответственно,
а выражения
, 
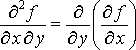– смешанными
частными производными второго
порядка функции 
.
Их обозначают также символами: 
, 
, 
и 
.
Аналогично определяют частные производные
3-го порядка (их будет 8=23 ),
4-го порядка (их будет 16=24 )
и т.д.
Теорема
4. Если
в некоторой окрестности точки
функция 
имеет
смешанные частные производные 
и 
,
причем эти производные непрерывны в
точке 
,
то они равны в этой
точке:
=
.
Если
последнее равенство выполняется, то
говорят, что смешанные частные производные
2-го порядка функции 
не
зависят от порядка дифференцирования
в точке 
.
Теорема 4 допускает обобщение: по индукции ее можно распространить на любые непрерывные смешанные частные производные.
30-Дифференцируемость и полный дифференциал функции. Необходимое и достаточное условия дифференцируемости функции.
Дифференцируемость
функции. Пусть 
.
Составим полное
приращение функции 
в
точке 
:
.
Определение.
Функция 
называется дифференцируемой в
точке 
,
если ее полное приращение в этой точке
можно представить в виде
, (1)
где 
и 
–
некоторые числа, 
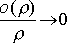при 
, 
.
Другими
словами, функция 
дифференцируема
в точке 
,
если ее приращение 
эквивалентно
функции 
: 
при 
.
Выражение 
в
этом случае представляет собой главную
часть приращения 
,
линейно зависящую от 
и 
.
Определение.
Если функция 
дифференцируема
в точке 
,
то главную линейную часть 
ее
приращения 
называют полным
дифференциалом в
точке 
и
обозначают в виде
.
Для
независимых переменных 
и 
полагают 
и 
.
Поэтому полный дифференциал записывают
также в виде
.
Формула (1) показывает, что, как и в случае функции одной переменной, верна
Теорема
5. Если
функция 
дифференцируема
в точке 
,
то она непрерывна в этой точке.
Обратное утверждение неверно, т.е. непрерывность является только необходимым, но не достаточным условием дифференцируемости функции. Покажем это.
Пример. 
Найдем
частные производные функции 
:
.
Полученные
формулы теряют смысл в точке 
.
Можно
показать иначе, что функция 
не
имеет частных производных в точке 
.
В самом деле, 
.
Эта функция одной переменной 
,
как известно, не имеет производной в
точке 
.
Последнее и означает, что частная
производная 
в
точке 
не
существует. Аналогично, не существует
частная производная 
.
При этом функция 
,
очевидно, непрерывна в точке 
.
^
Итак, мы показали, что непрерывная функция может не иметь частных производных. Осталось установить связь между дифференцируемостью и существованием частных производных.
31-применение полного дифференциала к приближенным вычислениям
Составьте
формулу, дающую при малых абсолютных
значениях величин x, y, z приближённое
выражение
Решение:
Так как найти полный дифференциал легче, чем полное приращение функции, то в
вычислениях используют приближенную формулу:
где
Представлю
заданное выражение
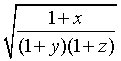
в виде:
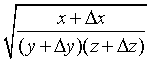
,где x=1; y=1 и z=1, а x, y и z заменю на Δx, Δy и Δz
Для приближённого вычисления значения функции трёх переменных можно использовать формулу:
Получу приближённое значение (x=1, y=1, z=1):
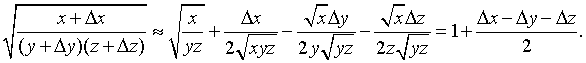
Для исходного выражения получим результат:
32-Дифференциалы высших порядков
Пусть в интервале (a, b) задана дважды дифференцируемая функция y = f(x), где x — независимая переменная.
Фиксируем приращение dx = Δx независимой переменной x, т.е. будем считать первый дифференциал
|
|
dy = f'(x) dx |
(1) |
функцией только переменной x.
Дифференциал от первого дифференциала, при условии, что повторное приращение независимой переменной x совпадает с первоначальным, называется вторым дифференциалом функции f(x) в точке x и обозначается d2 f(x).
Дифференцируем выражение в правой части (1) как произведение
|
|
d2 f(x) = d (df(x) ) = d (f'(x) dx) = f''(x) dx · dx + f'(x) · d(dx) . |
|
Учитывая, что d (dx) = 0, получаем формулу для вычисления второго дифференциала
|
|
d2 f(x) = f ''(x) dx2 . |
(2) |
Пусть в интервале (a, b) функция f(x) имеет производные до n–го порядка включительно.
Дифференциалом n–го порядка называется дифференциал от дифференциала (n − 1)–го порядка
|
|
dn f(x) = d (d(n − 1) f(x)). |
|
Формула для вычисления дифференциала n–го порядка
|
|
dn f(x) = f(n) (x) dxn . |
|
33-Производная сложной функции. Полная Производная.
Переменная z называется сложной функцией от независимых переменных х,у, t ,… если она задана посредством промежуточных аргументов u,v,…, где u = f(x ,y,t …), v = g ( x , y , t …) и.т.д.
Если для функции двух переменных z=f(x,y) обе переменные х и у зависят от некоторой третьей переменной t:х=j(t),у=c(t), то z зависит также только от t и можно вычислить производную причем справедлива теорема:
Теорема. Если функции x=x( t ) и =y( t ) дифференцируемы в точке t , а функция z=f( x , y ) дифференцируема в точке М( x ( t ), y ( t )), то сложная функция z=f ( x ( t ), y ( t )) также дифференцируема в точке t :
Из этой формулы можно вывести и формулы дифференцирования для других форм задания сложных функций.
Для функции двух переменных z =f(x,y ) в случае, когда х=х(u ,v), у=у( u , v ), производные сложной функции z=f(х( u , v ),у( u , v )), по переменным u и v считаются по формулам:
Если z = f(x,y) и у=у(х), то можно вычислять полную производную функции z по переменной х:
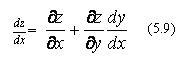
34-Инвариантность формы полного дифференциала
Инвариантность формы полного дифференциала .
Пусть дана фун-я z=f(x,y),тогда полным диф-ом фун-и z :
dz=(∂z/∂х)dx+(∂z/∂у)dу
Пусть теперь дана фун-я z=f(U, V), a U=U(x, y) V=V(x, y), тогда полный диф-ал dz=(∂f/∂х)dx+(∂f/∂у)dу=(∂f/∂U*∂U/∂х+ ∂f/∂V*∂V/∂y)dx+(∂f/∂U*∂U/∂х+∂f/∂V*∂V/∂y)dу=∂f/∂U([∂U/∂х]dx + +[∂U/∂y]dу)+∂f/∂V([∂V/∂х]dx +[∂V/∂y]dу)= (∂f/∂U)dU+(∂f/∂V)dV
Из полученного ⇒ что полный диф-ал ф-ии нескольких перемен- ных равен сумме произведений частных производных на соответст- вующие диффер-лы аргуменнтов и независимо от того явл-ся ли переменными или фун-ми. В этом и состоит инвариантность формы полного дифференциала.
35-Дифференцирование неявной функции. Теорема существования неявной функции.
Теорема 1. Пусть функция F(x,y) удовлетворяет условиям
F(x0,y0) = 0 ;
частные производные F'x и F'y непрерывны в некоторой окрестности точки (x0,y0) ;
F'y(x0,y0) ≠ 0 .
Тогда
уравнение F(x,y) = 0 определяет неявно в некоторой окрестности точки x0 единственную непрерывную функцию y(x) , удовлетворяющую условию y(x0) = y0 .
функция y(x) имеет производную, непрерывную в окрестности точки x0 .
Выясним смысл условий теоремы.
Существование непрерывной неявной функции y = f(x) в окрестности точки (x0, y0) следует из теоремы существования, так как:
условие 1 гарантирует существование точки, координаты которой удовлетворяют уравнению F(x,y) = 0 ;
из условия 2 следует непрерывность функции F(x,y) в окрестности точки (x0,y0) , а из условия 3 — ее монотонность по y при каждом фиксированном x из этой окрестности.
Следовательно, условия 1–3 обеспечивают выполнение условий существования неявной функции y(x) , удовлетворяющей условию y(x0) = y0 и непрерывной в окрестности точки x0 .
36-Касательная плоскость и нормаль к поверхности.
Касательной
плоскостью к поверхности 
в
данной точке P (x0,
y0,
z0) называется
плоскость, проходящая через точку Р и
содержащая в себе все касательные,
построенные в точке Р ко всевозможным
кривым на этой поверхности, проходящим
через точку Р.
Пусть поверхность s задана уравнением F (х, у, z) = 0 и точка P (x0, y0, z0) принадлежит этой поверхности. Выберем на поверхности какую-либо кривую L, проходящую через точку Р.
Пусть х = х(t), у = у(t), z = z(t) – параметрические уравнения линии L.
Предположим, что: 1) функция F(х, у, z) дифференцируема в точке Р и не все её частные производные в этой точке равны нулю; 2) функции х(t), у(t), z(t) также дифференцируемы.
Поскольку кривая принадлежит поверхности s , то координаты любой точки этой кривой, будучи подставленными в уравнение поверхности, обратят его в тождество. Таким образом, справедливо тождественное равенство: F [x(t), у(t), z (t)] = 0.
Продифференцировав это тождество по переменной t, используя цепное правило, получим новое тождественное равенство, справедливое во всех точках кривой, в том числе и в точке P (x0, y0, z0):
.
Пусть точке Р соответствует значение параметра t0, то есть x0 = x (t0), y0 = y (t0), z0 = z (t0). Тогда последнее соотношение, вычисленное в точке Р, примет вид
.
(17)
Формула (17) представляет собой скалярное произведение двух векторов. Первый из них – постоянный вектор
,
не
зависящий от выбора кривой на
поверхности 
.
Второй
вектор 
–
касательный в точке Р к
линии L,
а значит, зависящий от выбора линии на
поверхности, то есть является переменным
вектором.
При
введённых обозначениях равенство (17)
перепишем как 
.
Его смысл таков: скалярное произведение
равно нулю, следовательно,
векторы 
и 
перпендикулярны.
Выбирая всевозможные кривые (см. рис.
54), проходящие через точку Р на
поверхности s , мы будем иметь различные
касательные векторы, построенные в
точке Р к
этим линиям; вектор же 
от
этого выбора не зависит и будет
перпендикулярен любому из них, то есть
все касательные векторы
расположены
в одной плоскости, которая, по определению,
является касательной к поверхности s
, а точка Р в
этом случае называется точкой касания.
Вектор 
является
направляющим вектором нормали к
поверхности.
Определение 2. Нормалью к поверхности s в точке Р называется прямая, проходящая через точку Р и перпендикулярная к касательной плоскости, построенной в этой точке.
Мы доказали существование касательной плоскости, а, следовательно, и нормали к поверхности. Запишем их уравнения:
;
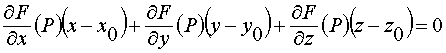(18)
(18) – уравнение касательной плоскости, построенной в точке P (x0, y0, z0) к поверхности s , заданной уравнением F(х, у, z) = 0;
;
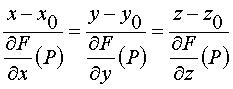(19)
– уравнение нормали, построенной в точке Р к поверхности s .
37-Экстремум функции двух переменных. Необходимое и достаточное условия экстремума.
Точка
называется
точкой максимума (минимума)
функции
(х,
у), если
Максимумы и минимумы функции называются ее экстремумами (рис. 12.1).
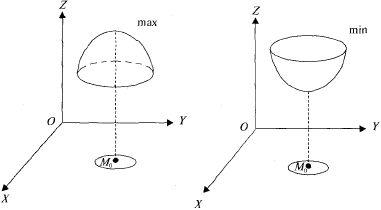
Рис. 12.1
Примеры:
1)
Очевидно т. (1, 2) является т. mm, так как все остальные значения х и у дадут z > -1
2)
В
данном случае т.
(0,
0) является т. max, так как
Т: (необходимое условие экстремума)
Если
функция г =
(х,у)
имеет экстремум в т.
то
или
обращаются в нуль, или не существуют
Пусть
у =
тогда
—
функция одной переменной. Так как при
х =
она
имеет экстремум, то
Доказательство
при х =
аналогично
Эти условия не являются достаточными.
Пример:
обращаются
в нуль в т. О(0,0),
но ху > 0 при х > 0, у > 0, ху < 0 при х < 0, у > 0, т.е. определение экстремума не выполняется.
Приведем достаточные условия экстремума для стационарных
т.
в
которых
Т:
(достаточные условия экстремума) Пусть
в некоторой области, содержащей
т.
функция
имеет
непрерывные частные производные до
третьего порядка включительно и эта
точка является стационарной.
Пусть
Доказательство см. в [11. С. 419].
Пример:
Исследовать на экстремум
—
стационарные
точки,
1)
—
точка минимума,
2)т.
—
точка
максимума,
3)
экстремума
нет,
4)
экстремума
нет
Для
функции п переменных
определение
экстремума и
необходимые
условия сохраняются. Необходимое
условие в случае дифференцируемой
функции
кратко
запишется в виде:
Сформулируем достаточные условия экстремума.
Т:
Если в стационарной т.
второй
дифферен-
циал
является
положительно (отрицательно) определенной
квадратичной формой, то
—
точка min (max)
Доказательство см. в [11. С. 424].
Сформулированные
ранее достаточные условия экстремума
для функции
являются
следствием данной теоремы.
38-наибольшее и наименьшее значение функции в замкнутой области.
Пусть в замкнутой области D задана функция z=z(x,y), имеющая непрерывные частные производные первого порядка. Граница Г области D является кусочно гладкой (т. е. состоит из кусков "гладких на ощупь" кривых или прямых). Тогда в области Dфункция z(x,y) достигает своего наибольшего M и наименьшего m значений.
Без доказательства.
Можно предложить следующий план нахождения M и m. 1. Строим чертёж, выделяем все части границы области D и находим все "угловые" точки границы. 2. Находим стационарные точки внутри D. 3. Находим стационарные точки на каждой из границ. 4. Вычисляем во всех стационарных и угловых точках, а затем выбираем наибольшее M и наименьшее m значения.
Пример 1.14 Найти наибольшее M и наименьшее m значения функции z = 4x2-2xy+y2-8x в замкнутой области D, ограниченной: x = 0, y = 0, 4x+3y=12 .
Решение
1. Построим область D (рис. 1.5) на плоскости Оху.
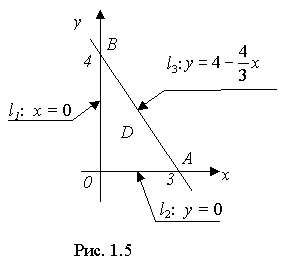
Угловые точки: О (0; 0), В (0; 4), А (3; 0).
Граница Г области D состоит из трёх частей:
2. Найдём стационарные точки внутри области D:
3. Стационарные точки на границах l1, l2, l3:
4. Вычисляем шесть значений:
Из полученных шести значений выбираем наибольшее и наименьшее.
Ответ:
39-двойные интегралы. Достаточное условие интегрируемости функции. Геометрический и фезический смысл двойного интеграла.
Двойным
интегралом называют кратный интеграл
с 
.
.
Здесь 
—
элемент площади в рассматриваемых
координатах.
В
прямоугольных координатах: 
,
где 
—
элемент площади в прямоугольных
координатах.