Для неопределённого интеграла

Функции и гладкие, следовательно, возможно дифференцирование:

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

Операция интегрирования обратна дифференцированию:

После перестановок:

Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во время интегрирования.

Типичную ошибку «потери» константы при обращении с неопределенным интегралом иллюстрирует следующий пример-софизм:

Отсюда «следствие»: , что очевидно неверно.

Для определённого интеграла

В целом аналогично случаю неопределённого интеграла:

Пример

19-Интегрирование четных и нечетных функций в симметричных пределах

Пусть функция ƒ(х) непрерывна на отрезке [-а; а], симметричном относительно точки х = 0. Докажем, что

Разобьем отрезок интегрирования [-а; а] на части [-а; 0] и [0; а]. Тогда по свойству аддитивности

В первом интеграле сделаем подстановку х = -t. Тогда

(согласно свойству: «определенный интеграл не зависит от обозначения переменной интегрирования»). Возвращаясь к равенству (39.4), получим

Если функция ƒ(х) четная (ƒ(-х) = ƒ(х)), то ƒ(-х) + ƒ(х) = 2ƒ(х); если функция ƒ(х) нечетная (ƒ(-х) = - ƒ(х)), то ƒ(-х) + ƒ(х) = 0. Следовательно, равенство (39.5) принимает вид (39.3).▲

Благодаря доказанной формуле можно, например, сразу, не производя вычислений, сказать, что

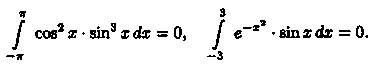
20-несобственные интегралы 1 рода их сходимость и расходимость

Абсолютная и условная сходимость несобственных интегралов от разрывных функций определяется аналогично тому, как это было сделано для несобственных интегралов по бесконечному промежутку ( 12.1.4) , а именно: несобственный интеграл от неограниченной функций называется абсолютно сходящимся, если сходится интеграл , и условно сходящимся, если интеграл сходится, а интеграл расходится (если сходится , то тоже обязательно сходится).  Пример: Исследовать на сходимость интеграл:  26. Так как , то исходный интеграл сходится абсолютно.

При отсутствии абсолютной сходимости установить условную сходимость можно с помощью признаков Абеля и Дирихле:  Признак Дирихле. Интеграл сходится, если:  1).функция f(x) непрерывна и имеет ограниченную первообразную на (a, b];  2).функция g(x) непрерывно дифференцируема и монотонна на (a, b], причём.

Признак Абеля. Интеграл сходится, если:  1).функция f(x) непрерывна на (a, b] и интеграл сходится;  2).функция g(x) ограничена, непрерывно дифференцируема и монотонна на (a, b], то есть имеет конечный предел:.

23- Приложения определенного интеграла: площадь плоской фигуры в декартовых, полярных, параметрических координатах; вычисление длины дуги плоской кривой в декартовых полярных параметрических координатах, вычисление объема тела вращения вычисление площади поверхности вращения

Площадь плоской области.

. Декартовы координаты. В пункте 11.1.4. мы сформулировали Геометрический смысл определённого интеграла: если f(x)>0 на отрезке [a,b],

то равен площади криволинейной трапецииABCD, ограниченной снизу отрезком [a,b], слева и справа - прямыми x = a и x = b , сверху - функцией y = f(x) . Следствие: если фигура ограничена сверху кривой y = f(x) , снизу - кривой y = g(x) , слева и справа - отрезками прямых x = a и x = b, то её площадь равна .Пример: Найти площадь областиD, ограниченной кривыми y = x² + x + 11, y = 2 x - 9, при условии, что (дальше мы будем писать так:).При решении таких задач следует обязательно изобразить исследуемый геометрический объект. Для определения нижнего предела интегрирования надо найти точку пересечения кривых;уравнениеx² + x + 11 = 2 x - 9 имеет два корня: x = -1 и x = 2. Подходящий корень - x = -1. Область ограничена сверху параболой, снизу - прямой, справа - прямой x = 1, крайняя левая точка - x = -1, поэтому Если область имеет более сложную структуру, её следует разбить на простые части .13.2.2. Область задана в полярных координатах.. Если область D - сектор, ограниченный лучами ,и кривой, формула для вычисления площади получается с помощью следующей интегральной конструкции. Разобьём промежутоклучаминаn частей; . На каждом из отрезковвыберем произвольную точку, найдём, тогдаравно площади сектора круга, ограниченного лучами,и дугой окружности радиуса. Объединение этих секторов - снова ступенчатая фигура, приближающая данную областьD, её площадь . Приразница междуS_ступ и S - площадью области D - будет тоже стремиться к нулю, т.е..Примеры: 1. Найти площадь, ограниченную лемнискатой.Решение: точки лемнискаты расположены в секторахи; кроме того, при решении таких задаче целесообразно использовать симметрию фигуры, поэтому мы найдём площадь части, расположенной в сектореи учетверим её:.2. Найти площадь, лежащую внутри кардиоидывне окружности.Решение: найдём разность площадей, лежащих внутри кардиоиды и окружности. Для верхней части кардиоиды; для верхней части окружности, поэтому3. Найти площадь, лежащую внутри окружностивне лемнискаты.Решение. Точки пересечения лемнискаты и окружности находятся из условия,Область симметрична относительно полярной оси, поэтому вычисляем площадь верхней части и удваиваем её. При измененииотдополярный радиус меняется отдо; при измененииотдополярный радиус меняется от 0 до; поэтому Область ограничена кривыми, заданными параметрически. Если кривая, ограничивающая криволинейную трапецию ABCD (см. 11.1.1. Вычисление площади криволинейной трапеции) задана в параметрическом виде ; то переход в интеграле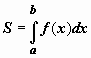к переменнойt приводит к формуле .Пример: найти площадь, ограниченную астроидой().Решение: используем симметрию фигуры. Мы найдём площадь части фигуры, расположенной в первом квадранте (), и учетверим её. Точка (0,a) получается при , точка (a, 0) - при t = 0, поэтому  

Вычисление длин кривых.

13.3.1. Определение спрямляемой кривой и длины кривой. Пусть на плоскости задана кривая AB. Разобьём эту кривую точками A = M₀, M₁, M₂, …, M_i-1, M_i, …, M_n = B на n частей и впишем в кривую ломаную M₀ M₁ M₂ …M_i-1 M_i … M_n, соединяющую эти точки. Длина L _лом этой ломанной равна сумме длин прямолинейных звеньев, соединяющих точки разбиения: . Устремим теперь количествоn точек разбиения к бесконечности так, чтобы максимальная длина звена стремилась к нулю. Если при этом существует конечный предел последовательности длин ломаныхL _лом, не зависящий от способа разбиения кривой, то кривая называется спрямляемой, а значение этого предела называется длиной кривой AB.  13.3.2. Длина кривой в декартовых координатах. Пусть теперь кривая AB - график функции кривой y = f(x), имеющей непрерывную производную ,. Тогда точкаM _i имеет координаты (x_i, f(x_i)), звено M_i-1M _i имеет длину . Функцияy = f(x) на отрезке [x_i-1x_i] удовлетворяет условиям теоремы Лагранжа, поэтому существует точка такая, что. С учётом этого длина звенаM_i-1M_i равна , длина всей ломаной -. Последняя сумма - интегральная сумма для интеграла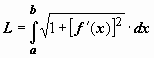, и, вследствие непрерывности подынтегральной функции, стремится к нему при. Итак, длина кривой, заданной декартовым уравнениемy = f(x), , определяется формулой.Пример: Найти длину отрезка параболыy = x² от точки A(0,0) до точки B(2,4).  Решение:, поэтому.3.3.3. Кривая задана параметрически . Заменим в переменнуюx на переменную t. Так как , то. Итак, длина кривой, заданной параметрически, определяется формулой.Пример: найти длину участка развёртки окружности, соответствующего одному витку нити.Решение: кривая задаётся уравнениями.13.3.4. Кривая задана в полярных координатах. Случай, когда кривая задаётся уравнением ,, легко сводится к предыдущему. Так как, то, рассматривая полярный уголкак параметр, получим, поэтому

.  Пример: найти длину кардиоиды.Решение:, поэтому. Ответ явно бессмысленен. Где ошибка? Ошибка в том, что упущен знак модуля при извлечении корня из. Правильное решение:Однако, как и в предыдущих случаях, проще воспользоваться симметрией фигуры, найти длину верхней ветви и удвоить её: