8. Приближенное решение игры методом итераций.

На практике часто нет необходимости находить точное решение игры, достаточно найти средний выигрыш игроков, близкий к цене игры. В таком случае можно получить прибиженное решение с помощью численного метода итераций.

Идея метода такова. Разыгрывается мысленный эксперимент, в котором игроки применяют друг против друга свои стратегии. Эксперимент состоит из последовательности элементарных игр с заданной платежной матрицей. Сначала первый игрок выбирает произвольную стратегию, например, . Второй игрок отвечает той стратегией, которая дает наименьший выигрыш для первого игрока при его стратегии. Первый игрок отвечает той своей стратегией, которая дает ему максимальный выигрыш при стратегиивторого игрока. Теперь второй игрок отвечает на пару стратегийипервого игрока той своей стратегией, которая дает минимальный суммарный выигрыш при стратегияхипервого игрока, и так далее. На каждом шаге итерационного процесса каждый игрок отвечает на очередной ход другого игрока той своей стратегией, которая обеспечивает минимальный суммарный выигрыш противника при всех его предыдущих стратегиях.

Если итерационный процесс продолжается достаточно долго, то средний выигрыш, приходящийся на одну игру, будет стремиться к цене игры, а частоты , с которыми игроки выполняют свои стратегии, будут приближаться к частотам, определяющим оптимальные стратегии.

Проиллюстрируем этот метод на примере игры Эдварда и Фионы, которая задана платежной матрицей : .

Пусть Эдвард вначале выбирает первую стратегию. Тогда Фиона выбирает свою вторую стратегию, определяющую наименьший выигрыш Эдварда при его первой стратегии. В ответ на это Эдвард выберет свою вторую стратегию, при которой он получает максимальный выигрыш при второй стратегии Фионы.

Теперь Фиона складывает выигрыши Эдварда почленно при его двух выбранных стратегиях (получается строка: -1, 1) и выбирает первую стратегию, при которой Эдвард получает минимальный выигрыш и т.д. Выполним этот процесс 10 раз, и результаты представим в таблице:

n	i			j
1	1	2	–	2	–3		0.5
2	2	–	1	1	–1		0
3	2	–	5	1		–2	–0.5
4	1	–	2	1		–5	0.125
5	1	0	–	2		–1	–0.1
6	1	2	–	2	–3		–0.083
7	2	–	0	1	–1		–0.071
8	2	–	4	1		–3	–0.188
9	1	–	1	1		–6	0.055
10	1	0	–	2	0	–	0

В первом столбце таблицы записан номер элементарной игры n, во втором – номер i выбранной стратегии первого игрока, в следующих двух – «накопленнный» выигрыш за первые n игр второго игрока при его стратегиях , . Минимальное из этих значений подчеркнуто. В пятом столбце записан номер j стратегии, выбранной вторым игроком. В следующих двух столбцах записан «накопленнный» выигрыш за первые n игр первого игрока при его стратегиях , . Максимальное из этих значений надчеркнуто. В последнем столбце вычисляется средний накопленный выигрыш V, приходящийся на одну игру.

Частоту каждой стратегии можно вычислить, разделив на 10 количество строк, где применяется игроком эта стратегия. Таким образом, приближенными оптимальными стратегиями Эдварда и Фионы будут смешанные стратегии:

и

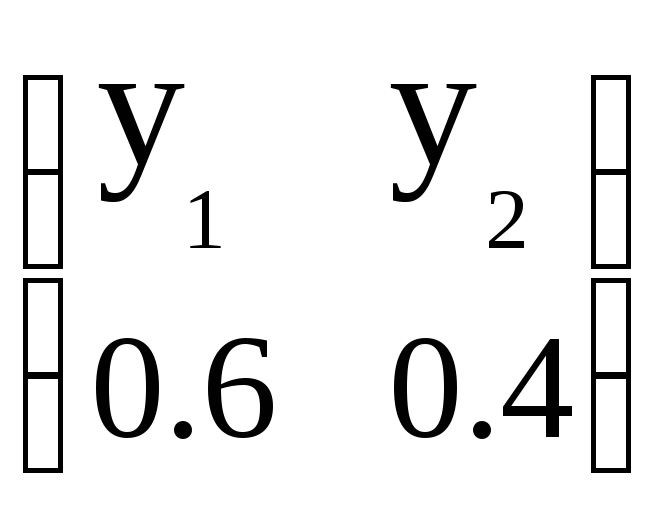
Приближенное значение цены игры: V = 0. Получились довольно грубые приближения оптимальных стратегий игроков и цены игры, но если применить компьютер, и количество элементарных игр увеличить до числа g = 20000, получим результаты, совпадающие с точными, если оставить в записи чисел 3 цифры после запятой:

и и V = – 0.083

20