5. Геометрическая интерпретация игры размера 2×2

Решение игры размера 2×2 допускает наглядную геометрическую интерпретацию. Пусть игра не имеет седловой точки и задана платежной матрицей:

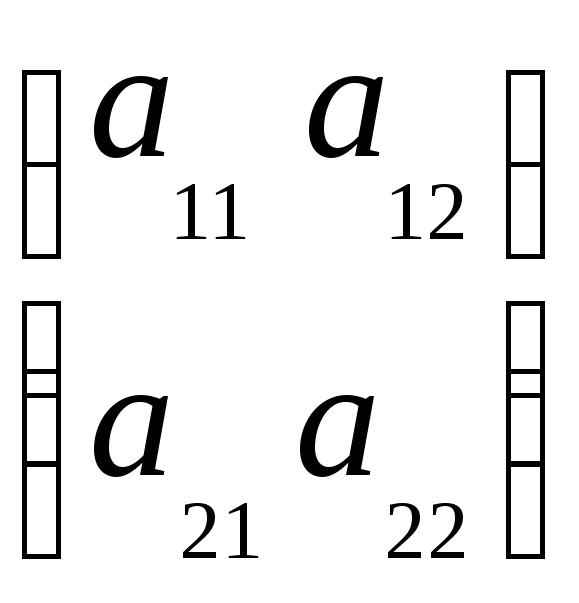
Если второй игрок применяет свою первую стратегию, то выигрыш первого игрока определяется формулой:

;

Аналогично, если второй игрок применяет свою вторую чистую стратегию, то выигрыш первого игрока определяется формулой:

;

Из формул (1) и (2) видно, что выигрыши первого игрока при чистых стратегиях второго игрока являются линейными функциями с аргументом .

Построим графики функций ина отрезке [0, 1] изменения частоты :

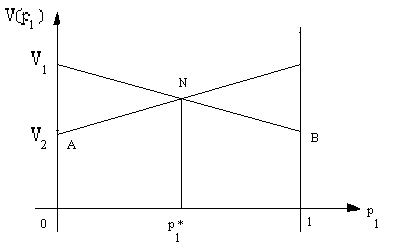
Рис. 9.1

В соответствии с принципом минимакса для смешанных стратегий, первый игрок должен выбрать частоту так, чтобы максимизировать свой выигрыш. Ординаты точек ломаной ANB показывают минимальный его выигрыш при использовании им любой смешанной стратегии. Ломаная ANB является нижней границей выигрышей первого игрока. Оптимальную стратегию определяет точка N, в которой минимальный выигрыш достигает максимума. Это самая верхняя точка нижней границы выигрышей первого игрока. Ее ордината равна цене игры V. Координаты точки N являются решением системы уравнений (1) и (2).

Заметим, что в игре размера 2×2 без седловой точки прямые иимеют противоположные наклоны, т.е. одна прямая составляет острый угол с осью ,другая – тупой, в противном случае игра будет иметь седловую точку, и решение игры будет в чистых стратегиях.

Применим геометрический метод для решения игры Эдварда и Фионы, заданной платежной матрицей 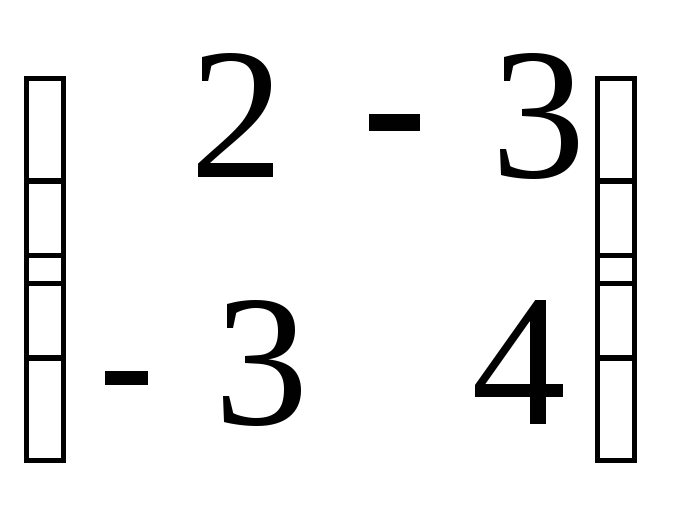. Чтобы найти цену игры и оптимальную стратегию Эдварда, достаточно найти координаты точки N, для чего составим систему уравнений из формул (1) и (2):

Решив систему, найдем, что , , .

6. Решение игры размера 2×n

Для решения игры, в которой хотя бы один игрок имеет только две стратегии, можно воспользоваться следующей теоремой, имеющей место в теории игр:

Теорема 4. Любая конечная игра размера m×n имеет решение, в котором число активных стратегий у каждого игрока не превосходит наименьшего из чисел m и n.

Из этой теоремы следует, что у игры размера 2×n всегда имеется решение, в котором каждый игрок использует не более двух активных стратегий.

Пользуясь геометрической интерпретацией, можно дать простой способ решения игры размера 2×n без седловой точки. Пусть платежная матрица игры имеет вид:

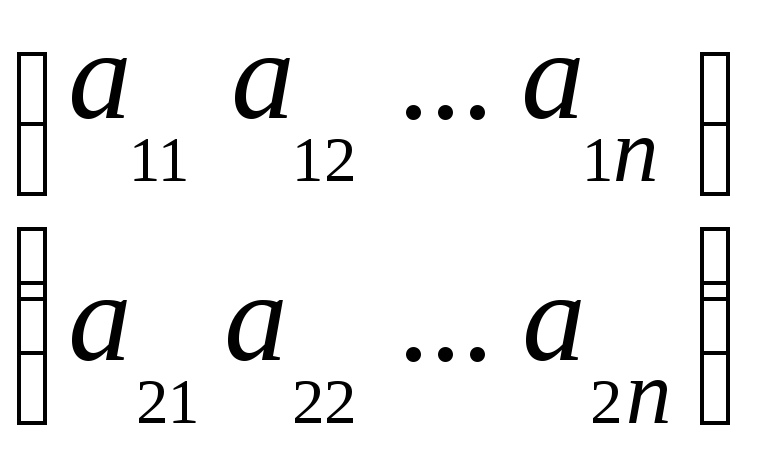
Для каждой из n чистых стратегий второго игрока строим график функции выигрыша первого игрока по формуле:

(1) ;

Непосредственно по чертежу находим пару активных стратегий второго игрока, соответствующих двум графикам функций выигрыша, пересекающихся в точке с максимальной ординатой на нижней границе выигрышей и имеющих противоположные наклоны. Вместе со стратегиями первого игрока они образуют по теореме 4 игру размера 2×2, решение которой является решением и исходной игры.

Пример 3. Инга и Кора играют в следующую игру: Кора прячет в кулаке либо 1, либо 2, либо 3, либо 4 монеты (достоинством в 1 доллар). Инга угадывает: четное число монет или нечетное. Если она угадала, Кора отдает монеты, иначе Инга должна заплатить ту сумму, которая была в кулаке у Коры.

Решение. Составим платежную матрицу игры размера 2×4 и найдем нижнюю и верхнюю цену игры. = –3 ,= 1,  , следовательно, игра без седловой точки.

Кора Инга	1	2	3	4
чет	–1	2	–3	4	–3
нечет	1	–2	3	–4	–4
	1	2	3	4

Функции выигрыша Инги, соответствующие чистым стратегиям Коры вычисляем по формуле (1):

Построим графики функций на отрезке [0, 1] изменения частоты :

Рис. 9.2

Ломаная ANB является нижней границей выигрышей первого игрока, координаты точки N определяют оптимальную стратегию Инги и цену игры. Тока N – точка пересечения всех четырех графиков, в частности, ис противоположными наклонами, поэтому активными стратегиями Коры можно считать третью и четвертую стратегии. Получаем игру размера 2×2 с платежной матрицей: 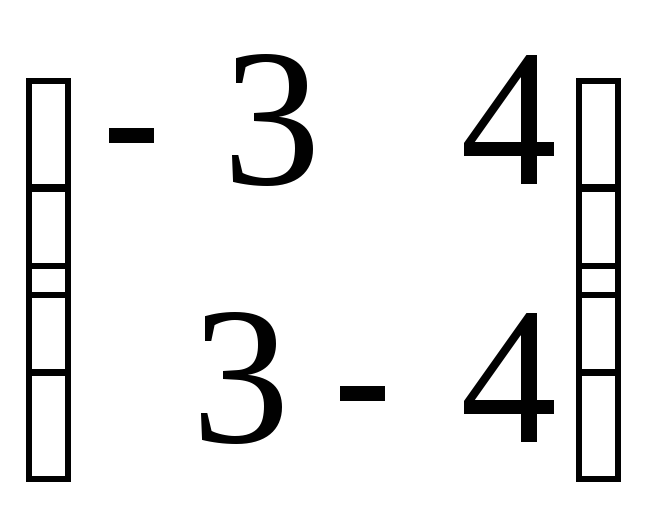, для которой находим, что =, = ,V = 0,=, = . Поэтому оптимальная стратегия Коры имеет вид:

.

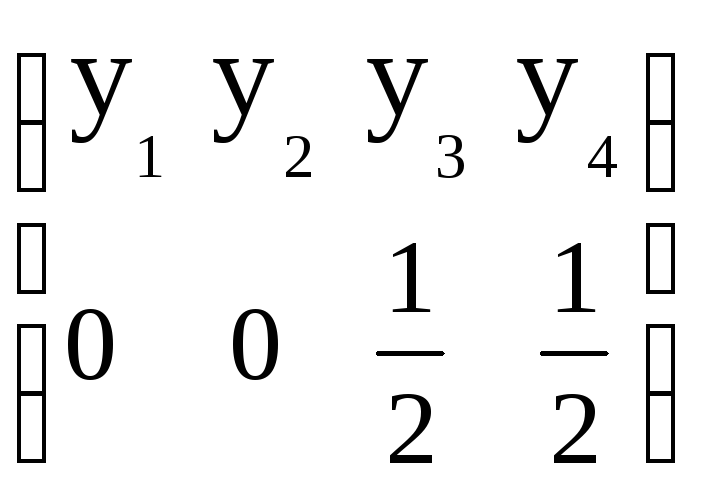Аналогично можно решить игру размера m×2, где m >2.