§1. Нелинейное программирование

Задачи оптимизации, в которых целевая функция не является линейной функцией своих аргументов или среди условий, определяющих их допустимые значения, могут быть нелинейные уравнения и неравенства, называются задачами нелинейного программирования. Нелинейное программирование широко применяется в экономике при управлении товарными ресурсами, планировании обслуживания и ремонта оборудования и послужило основой широкого использования математических методов в экономике. В качестве примеров рассмотрим две простейших задачи нелинейного программирования: задачу минимизации расходов при реализации продукции и задачу максимизации объема производства.

1. Задача минимизации расходов

Фирма реализует автомобили двумя способами: через розничную торговлю и оптом. При реализации автомобилей в розницу расходы на реализацию составляют условных единиц, а при продаже автомобилей оптом – таких же единиц. Найти оптимальный способ реализации 100 автомобилей, минимизирующий суммарные расходы.

Математическая модель задачи заключается в следующем:

Найти неотрицательное решение уравнения

+ =100 (

при котором функция

принимает минимальное значение.

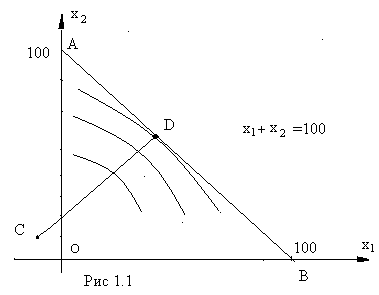
Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую интерпретацию.

Так как , то линиями уровня функции являются окружности разных радиусов с центром в точке C(-10, 10), а областью допустимых решений задачи – отрезок AB прямой + =100 (рис. 1.1).

Если проводить эти окружности из точки C, то нетрудно догадаться, что минимальное значение функция принимает в точке D касания окружности уровня с отрезком AB. Радиус этой окружности будет перпендикулярен прямой AB, поэтому угловой коэффициент k прямой CD равен единице: k=1. Следовательно, уравнение прямой CD имеет вид:

, или –= –20.

Решая систему уравнений

,

находим координаты точки D: = 40, = 60. Значит , фирма должна продать в розницу 40 автомобилей, а оптом – 60 автомобилей, при этом суммарные расходы составят 1600 + 800 + 3600 – 1200 = 4800 условных единиц.

2. Задача максимизации объема производства.

Для пошива пальто и курток швейная фабрика использует ткань двух типов. На изготовление одного пальто расходуется 2 м ткани первого типа и 1,5 м ткани второго типа. Для пошива куртки аналогичные данные составляют 1,5 м ткани первого типа и 1 м ткани второго типа. В распоряжении фабрики ежедневно имеется 300 м ткани первого типа и 180 м ткани второго типа. Ежедневный спрос на куртки не превышает 60 штук. Какое количество пальто и курток надо сшить, чтобы в рамках этих ресурсов прибыль фабрики, определяемая функцией ,была максимальной?

Для решения задачи снова построим математическую модель. Обозначим через и запланированное количество пальто и курток. Ограниченные запасы тканей и спрос на куртки означают, что переменные и должны удовлетворять системе неравенств:

(3)

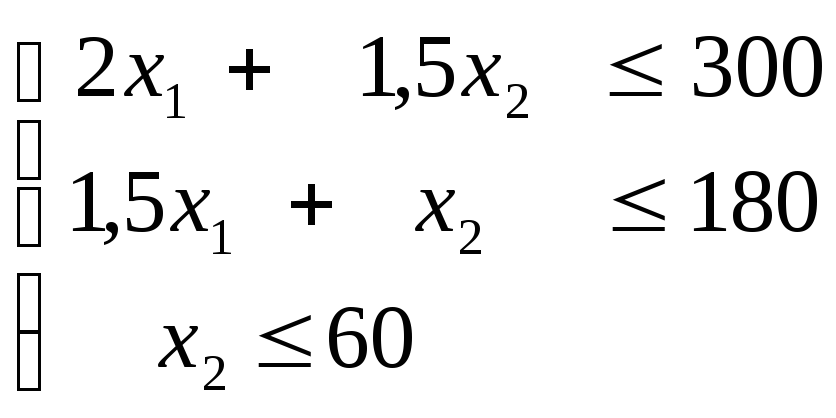
Кроме того, по смыслу задачи они должны быть неотрицательными:

(4) .

Прибыль фабрики по условию определяется формулой:

(5) +

Итак, математическая модель задачи такова: найти числа и , являющиеся решениями системы (3) и удовлетворяющие условию (4), при которых функция (5) имеет максимальное значение.

Так как целевая функция снова не является линейной, то эта задача, как и предыдущая, является задачей нелинейного программирования. Найдем ее решение, используя снова геометрическую интерпретацию.

Так как + =, то линиями уровня k функции являются параболы с вершинами в точках с координатами (40, ), где = – 1600 + k.

Условия (3) и (4) определяют четырехугольник OABC (рис 1.2), координаты точек которого являются неотрицательными решениями системы (3).

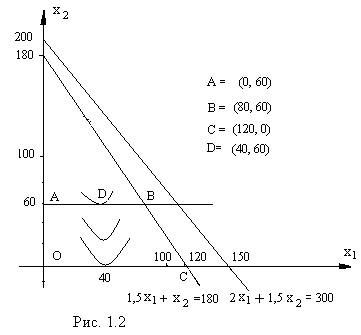
Поэтому функция принимает максимальное значение в точке касания одной из парабол с верхней границей четырехугольника OABC. Точка D(40, 60) является точкой касания искомой параболы с прямой AB.

max= (40, 60) = 1660.

В рассмотренных примерах точки, в которых целевая функция принимала оптимальное значение, не являлись вершинами многоугольника допустимых решений, и область допустимых решений не всегда является многоугольником. Поэтому метод перебора вершин многоугольника допустимых решений задачи линейного программирования и связанный с ним симплекс-метод неприменимы для решения задач нелинейного программирования.