7. Решение игры размера m×n с помощью линейного программирования

В общем случае игра размера m×n не имеет геометрической интерпретации, и для нее нет аналитического решения. Однако теория игр тесно связана с линейным программированием. Любая конечная игра с нулевой суммой может быть представлена в виде задачи линейного программирования и, наоборот, любая задача линейного программирования может быть представлена как конечная игра. Первым установил эту связь американский математик Д. Нейман. Покажем, как свести решение игры размера m×n к решению задачи линейного программирования.

Пусть игра задана платежной матрицей A:

A = 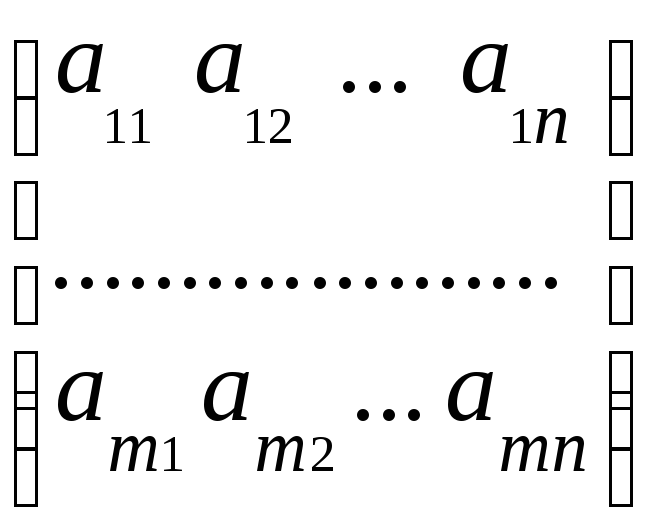,i = 1, 2, …, m; j = 1, 2, …, n.

Можно считать, что цена игры V > 0; этого можно добиться, увеличив все элементы матрицы A на достаточно большое положительное число k. При этом преобразовании матрицы A цена игры также увеличится на k. Оптимальная стратегия первого игрока 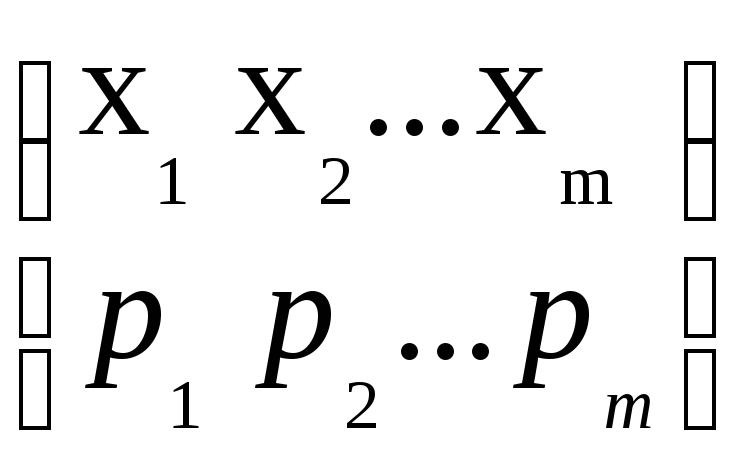, =1, обеспечивает ему средний выигрыш, не меньший, чем цена игрыV, при любой чистой j = 1, 2, …, n стратегии второго игрока, поэтому получаем систему n линейных неравенств:

(1)

Разделим каждое из неравенств на число > 0 и введем новые переменные, определяемые по формуле:

Так как = 1, то=. Система (1) примет вид:

(3)

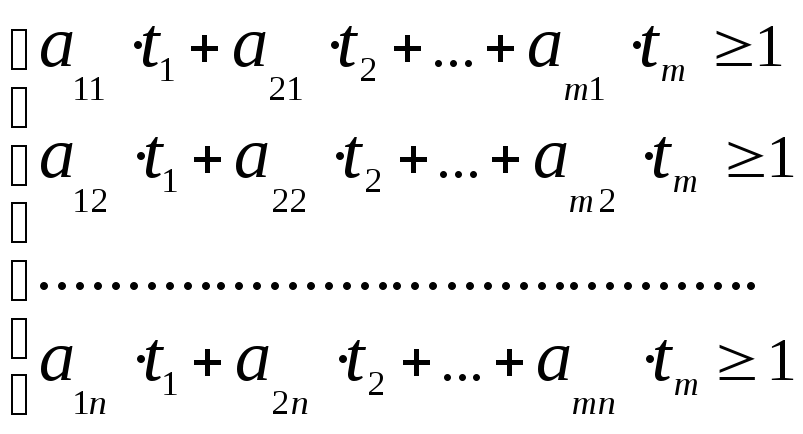
Цель первого игрока – максимизировать свой выигрыш, т.е. цену игры V. Это эквивалентно тому, что ему требуется минимизировать величину

=. Тогда задачу первого игрока можно сформулировать так: найти неотрицательные значения переменных , удовлетворяющие системе линейных неравенств (3), при которых линейная функция z = принимает минимальное значение. Мы получили задачу линейного программирования. Решив ее симплекс – методом, перейдем, используя формулы (2), к старым переменным и получим оптимальную стратегию первого игрока и цену игры V.

Для определения оптимальной стратегии второго игрока:

, =1,

следует учесть, что она обеспечивает ему средний проигрыш не больший, чем цена игры V, при любой чистой i = 1, 2, …, m стратегии первого игрока, поэтому получаем систему m линейных неравенств:

(4)

Разделим каждое из неравенств на число V > 0 и введем новые переменные , определяемые по формуле:

Так как =1, то=. Система (4) примет вид:

(6)

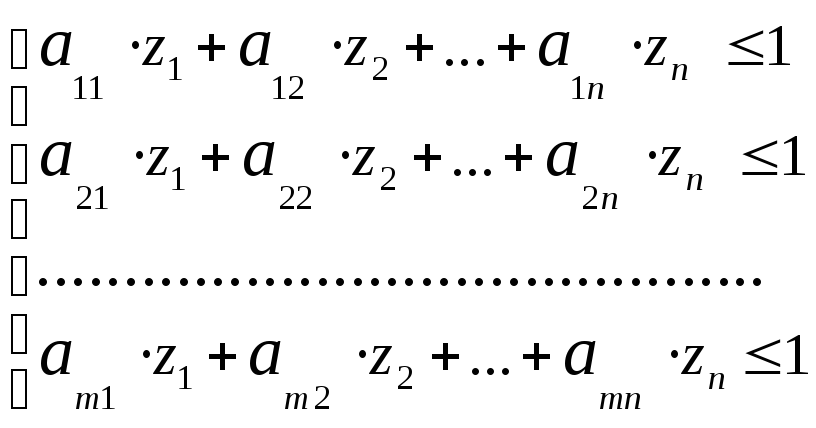
Цель второго игрока – минимизировать свой проигрыш, т.е. цену игры V. Это эквивалентно тому, что ему требуется максимизировать величину =. Тогда задачу второго игрока можно сформулировать так: найти неотрицательные значения переменных , удовлетворяющие системе линейных неравенств (6), при которых линейная функцияf = принимает минимальное значение. Мы снова получили задачу линейного программирования. Решив ее симплекс – методом, перейдем, используя формулы (5), к старым переменным и получим оптимальную стратегию второго игрока.

Отметим, что задача для второго игрока с системой ограничений (6) является двойственной к задаче первого игрока с системой ограничений (3).

Пример 4. Найти решение игры с платежной матрицей

A =

Для решения игры применим систему компьютерной алгебры Maple. Подключим модуль simplex, зададим систему неравенств (3) под именем sn, определим функцию z = t1+t2+t3 и найдем оптимальное решение задачи линейного программирования с помощью стандартной функции mininmize:

> with(simplex);

>sn:={7*t1+6*t2+5*t3>=1, 6*t1+7*t2+8*t3>=1, 7*t1+9*t2+4*t3>=1,

5*t1+8*t2+6*t3>=1};

> z:=t1+t2+t3;

> minimize(z, sn, NONNEGATIVE); {t3 = 0, t2 = 1/13, t1 = 1/13}

Так как t1+ t2 + t3 = 2/13 =, то цена игры V = 6,5 и, используя формулу (2), находим : t1*V = 0,5, t2*V = 0,5, 0.

Для вычисления оптимальной стратегии второго игрока, снова применим Maple, задавая систему (6) под именем cn и максимизируя функцию f = z1+z2+z3+z4:

> with(simplex);

>cn:={7*z1+6*z2+7*z3+5*z4<=1, 6*z1+7*z2+9*z3+8*z4<=1,

5*z1+8*z2+4*z3+6*z4<=1};

> f:=z1+z2+z3+z4;

> maximize(f, cn, NONNEGAT IVE}; {z2 =1/13, z1 =1/13, z4 = 0, z3 = 0}

Так как цена игры V = 6,5, то, используя формулу (5), находим:

z1*V = 0,5, t2*V = 0,5, 0, 0.

В некоторых случаях игру размера m×n можно упростить, удаляя «доминируемые» стратегии игроков. Стратегия с номером i первого игрока доминируется k – той его стратегией, если все элементы строки i платежной матрицы не больше соответствующих элементов строки k, т.е. дляj = 1,2, …, n. Поэтому доминируемая i – тая стратегия первого игрока хуже его k – тoй стратегии, и ее можно не использовать в игре. Аналогично определяется доминируемая стратегия второго игрока, приносящая ему больший проигрыш, чем другая его стратегия.

Пример 5. Найти решение игры с платежной матрицей

A =

Решение. Третья стратегия первого игрока доминируется второй, поэтому ее можно отбросить. После этого третья и четвертая стратегии второго игрока доминируются его второй стратегией, и их также можно удалить. Получаем игру размера 2×2 с платежной матрицей =. Эта игра без седловой точки и легко решается аналитически:, цена игры V=6,25, .