1.5. Комплексные числа

Понятие числа является одним из основных завоеваний человеческой культуры. Сначала появились натуральные числа N = {1, 2, 3, …, n, …} затем целые Z = {…, –2, –1, 0, 1, 2, …}, рациональные Q = { | m  Z, n  N} (для того чтобы всякое уравнение вида ах = b, где а ≠ 0 имело решение); потом появились иррациональные числа это было связано с решением квадратных уравнений, например х² = 2, на множестве рациональных чисел это уравнение не имеет решения. Иррациональные числа – это бесконечные непериодические десятичные дроби, например , е, , , …. Рациональные числа можно представить конечными или бесконечными периодическими десятичными дробями, например  = 0,2;  = 0,(3). Рациональные и иррациональные числа образуют множество R действительных чисел. На этом множестве уравнение х² = 2 уже имеет два корня х₁ =  и х₂ = –. Но действительных чисел оказалось недостаточно для того, чтобы, например решить квадратное уравнение вида х² + 1 = 0 (т. к. на множестве действительных чисел нет такого числа, квадрат которого отрицателен). Поэтому ввели комплексные числа C. Впервые упоминание о комплексных числах появилось в работах итальянского ученого Кардано⁵ в 1545 г., когда он пришел к выражению , решая кубическое уравнение х³ –12х + 16 = 0. Термин «комплексное число» ввел немецкий математики Гаусс⁶ в 1831 г. Первоначально комплексные числа называли мнимыми. И только когда датчанин Вессель⁷(1799 г.) (независимо от него француз Арган⁸ (1806 г.) и немец Гаусс (1832 г.)) дал геометрическое истолкование комплексного числа, они получили признание и нашли широкое применение.

Уравнение вида х² + 1 = 0 приводит к понятию мнимой единицы. Решая это уравнение, получаем х² = –1 или х = ; назвали мнимой единицей и обозначили i =  или i² = –1.

Определение 1.17. Комплексным числом называется выражение вида a + bi, где a, b  R, i =  – мнимая единица.

Комплексное число z = a + bi состоит из двух частей: число а = Rez– называется действительной частью z, b = Imz – мнимой частью комплексного числа z.

Используют следующие термины: если b = 0, то a + 0i = а – действительное число (точнее отождествляют с действительным числом), в частности 0 + 0i = 0; если а = 0, то числа вида bi (b ≠ 0) называют чисто мнимым. Множество всех комплексных чисел обозначают C = {a + bi | a, b  R, i = } при этом R  C.

Определение 1.18. Комплексное число, записанное в виде z = a + bi, называется алгебраической формой записи комплексного числа.

Определение 1.18. Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части равны, т. е. a + bi = с + di  a + с и b = d.

Определение 1.19. Комплексные числа вида a + bi и a – bi называются сопряженными.

Определение 1.20. Комплексные числа вида a + bi и –a – bi называются противоположными.

Операции над комплексными числами

1. Сложение: (a + bi) + (с + di) = (а + с) + (b + d)i, при сложении двух комплексных чисел их действительные части и мнимые части складываются.

2. Вычитание: (a + bi) – (с + di) = (а – с) + (b – d)i.

3. Умножение: (a + bi)(с + di) = (ас – bd) + (ad + bc)i, это простое умножение двучлена a + bi на с + di с последующей заменой i² на –1.

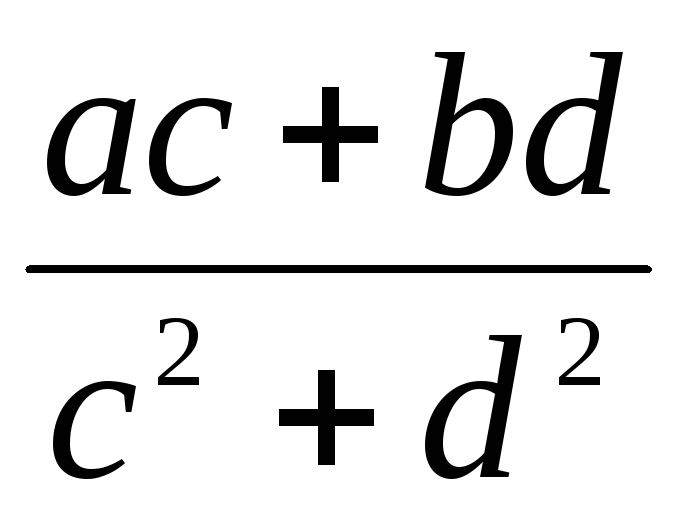4. Деление:  =  =  = + , если с + di ≠ 0.