1.2. Подмножества. Диаграммы Эйлера – Венна

Определение 1.4. Множество B называется подмножеством множества A, если каждый элемент множества B принадлежит множеству A.

Пример 1.2. Пусть А = {1, 2, 3, 4, 5, 6, 7}, а B = {2, 3, 5, 7}. Множество В является подмножеством множества А, поскольку каждый элемент множества В принадлежит множеству А.

Если множество B является подмножеством множества A, то говорят также, что B содержится в A или B включено в A, при этом пишут В  А или А  В. Символ  называется знаком включения (точнее, нестрого включения).

Согласно данному определению 1.4 подмножества, каждое множество является подмножеством самого себя, то есть ( A) А  А. Кроме того, считается, что пустое множество есть подмножество любого множества A: ( A)   А.

Различают два вида подмножеств множества А.

Определение 1.5. Пустое множество  и множество А называются несобственными подмножествами множества А.

Определение 1.6. Любые подмножества множества А, отличные от А и , называются собственными подмножествами множества А.

Определение 1.7. Множества A и B, состоящие из одних и тех же элементов, называются равными. При этом пишут А = В, в противном случае А ≠ В.

Справедливо следующее утверждение, которое также можно рассматривать в качестве определения равных множеств.

Утверждение 1.1. А = В  А  B и В  А.

Замечание 1.3. Из утверждения 1.1 вытекает способ доказательства равенства двух множеств: если доказать, что каждый элемент из множества A является элементом множества B и каждый элемент из множества B является элементом множества A, то делают вывод, что А = В.

Говорят, что множество B строго включено в множество A или, по-другому, А строго включает B, если В  А и В  А. В этом случае пишут B  A. Символ  называется знаком строгого включения.

Пример 1.3. Имеют место следующие строгие включения числовых множеств: N  N₀  Z  Q  R  C и I  R  C.

Определение 1.8. Совокупность всех подмножеств множества A называется его булеаном (или множеством-степенью), и обозначается через P(A) (или 2^A).

Пример 1.4. Если A = {a, b, c}, то булеан множества А это множество P(A) = {, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}}.

Для наглядного изображения множеств и их свойств используют так называемые диаграммы Эйлера² – Венна³. Множество отождествляется с множеством точек на плоскости, лежащих внутри некоторых замкнутых кривых, например окружностей (так называемые круги Эйлера). В частности, универсальное множество U изображается множеством точек некоторого прямоугольника или всей плоскости (рис. 1.1).

1.3. Операции над множествами и их свойства

Определим операции над множествами, с помощью которых можно получать из любых имеющихся множеств новые множества.

1. Объединение (или сумма).

Определение 1.9. Объединением множеств А и В называется множество A  B, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств.

То есть, по определению 1.9, A  B = {х | х Î А или х Î В}.

Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера – Венна. Объединение множеств А и В заштриховано и изображено на рис. 1.2.

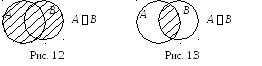
Заметим, что в объединение двух множеств A и B могут входить элементы из A, не принадлежащие множеству B, элементы из B, не принадлежащие множеству A, и элементы, принадлежащие множествам A и B одновременно. Следовательно, ( A, B) A  A  B и B  A  B.