3.2. Основные операции над матрицами и их свойства

3.2.1. Сложение однотипных матриц

Складывать можно только однотипные матрицы.

Определение 3.12. Суммой двух матриц А = (a_ij) и B = (b_ij), где i = 1, 2, …, m, j = 1, 2, …, n называется матрица С = (с_ij) для которой с_ij = a_ij + b_ij, где i = 1, 2, …, m, j = 1, 2, …, n. Обозначение: С = А + B.

Иначе говоря: сложение матриц производится поэлементно.

Пример 3.1. Для матриц А =  и В =  найти их сумму.

Решение. С = А + B =  +  = .

Свойства сложения матриц

1. коммутативность:  А, В : А + В = В + А;

2. ассоциативность:  А, В, С : (А + В) + С = А + (В + С);

3.  А, А + О = А, где О – нулевая матрица;

4.  А,  –А : А + (–А) = О, (–А) – матрица, противоположная матрице А.

Замечание 3.1. Пусть А = (a_ij) тогда –А = (–a_ij), где элемент –a_ij – противоположный элементу a_ij для любых индексов i и j, при этом матрица –А называется противоположной к матрице А.

Пример 3.2. Пусть А =  тогда –А = .

3.2.2. Умножение матрицы на число

Определение 3.13. Произведением матрицы А = (a_ij) на действительной число k называется матрица С = (с_ij), для которой с_ij = ka_ij, где i = 1, 2, …, m, j = 1, 2, …, n. Обозначение: С = kА = kА, т. о. каждый элемент матрицы А умножают на действительное число k.

Пример 3.3. Пусть дано число k = –2 и матрица А = , тогда kА = (–2) = .

Свойства умножения матрицы на число

1.  А : 1А = А;

2.  α, β  R,  А : (αβ)А = α(βА) = β(αА);

3.  α  R,  А, В : α(А + В) = αА + αВ;

4.  α, β  R,  А : (α + β)А = αА + βА.

3.2.3. Умножение матриц

Определим умножение двух матриц; для этого необходимо ввести некоторые дополнительные понятия.

Определение 3.14. Матрицы А и В называются согласованными, если число столбцов матрицы А равно числу строк матрицы В.

Например матрицы А размерности m  n и В размерности n  p будут согласованными.

Обозначим строки матрицы А как А₁, А₂, …, А_m, а столбцы матрицы В как B¹, B², …, B^p. При этом в строке матрицы А столько же элементов, сколько в столбце матрицы В. Это условие позволяет умножать строку матрицы А на столбец матрицы В.

Умножим, например, А₁ на столбец B¹. Пусть А₁ = (а₁ а₂ … а_n), B¹ = тогда А₁B¹ = (а₁ а₂ … а_n) = а₁b₁ + а₂b₂ + … + а_nb_n.

Пример 3.4. Умножим строку (1 2 3 4) на столбец . (1 –2 3 4) = (13 + (–2)2 + 31 + 40) = (2).

Теперь можно определить умножение матриц.

Определение 3.15. Произведением согласованных матриц А размерности m  n и В размерности n  p называется матрица С = (с_ij) размерности m  p, для которой с_ij = А_iB^j, где i = 1, 2, …, m, j = 1, 2, …, p.

Обозначение: С = AB = .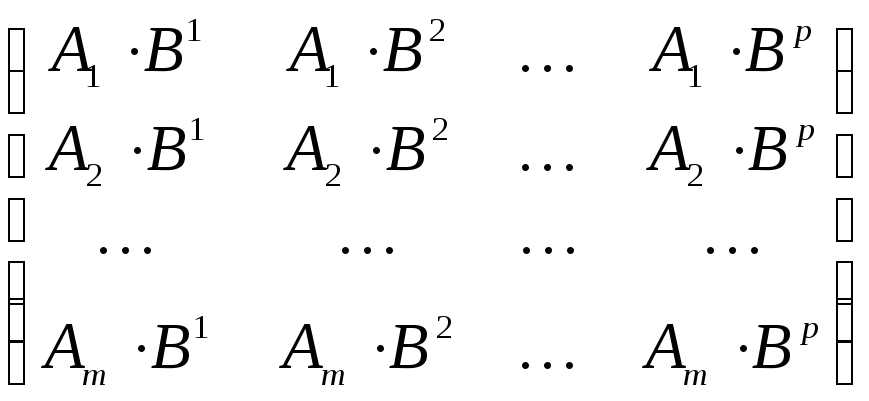

Пример 3.5. Найти произведение матриц АВ, где А = , В = .

Решение. Матрицы А_32 и В_24 согласованы, значит можно найти произведение этих матриц АВ, результатом будет матрица размерности 3  4. АВ =  =

=  = 

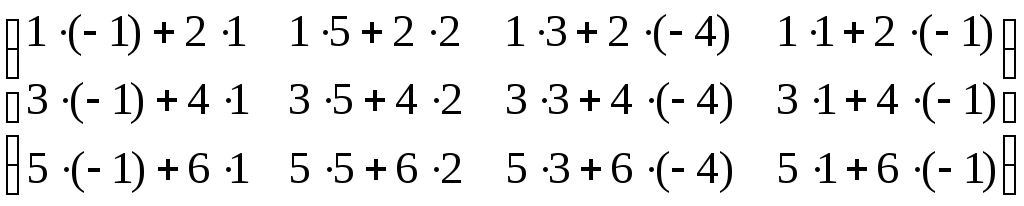Свойства умножения матриц

1. Умножение матриц не коммутативно: AB ≠ BA.

Продемонстрировать данное свойство можно на примерах.

Пример 3.6. а) Пусть даны две матрицы: А =  и В = . Перемножим матрицы AB =  =  = , получим матрицу размерности 2  1. Умножить матрицу В = В_21 на матрицу А = А_22 нельзя, так как эти матрицы не согласованные. Т. о. свойство коммутативности для умножения двух матриц не выполняется.

б) Возьмем две матрицы так, чтобы А и В были согласованы и чтобы также В и А были согласованные. Проверим, что при данных условиях свойство коммутативности также не выполняется. Пусть А = А_23 =  и В = В_32 = , найдем их произведения.

AB =  =  = С_22;

ВА =  =  = С_33.

2. Ассоциативность: (AB)С = А(ВС).

3. Для любой квадратной матрицы А и согласованной с ней единичной матрицы Е справедливо равенство: AЕ = ЕA.

4. Дистрибутивный закон умножения матриц относительно сложения матриц:  А, В, С : (A + B)С = (АС) + (ВС) и A(B + С) = (АВ) + (АС).

Пример 3.7. Пусть даны матрицы А = , В =  и С =  проверим справедливость свойства 4.

(A + B)С =  +  =  = ;

(АС) + (ВС) =  +  =  +  = .

5.  k  R,  А, В : k(АВ) = (kА)В = А(kВ).