
ТОЭ / ТОЭ ТПУ
.pdf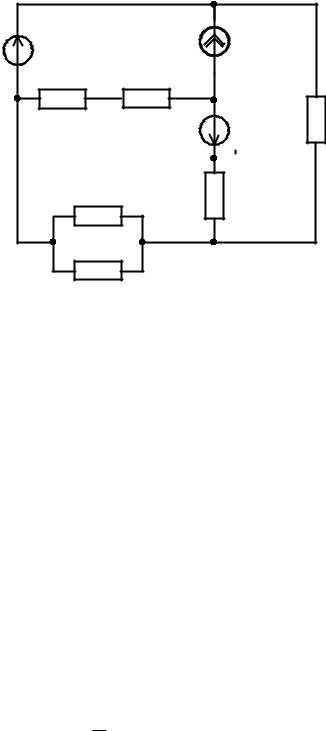
|
b |
E1 |
J |
|
|
R |
R |
a |
d |
|
R |
|
E2 |
|
d |
R R
R |
c |
|
Рис.5. Схема электрической цепи
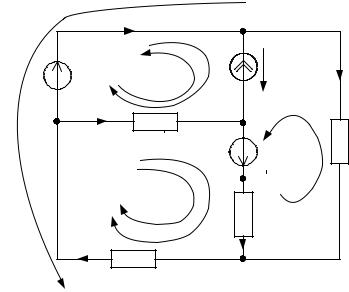
3.Выбираем положительные направления токов. В ветвях, содержащих ЭДС – по направлению ЭДС, в остальных ветвях – произвольно. Расчетная схема электрической цепи с указанными направлениями токов в ветвях и напряжением на источнике тока приведена на рис.6.
4.В общем (буквенном) виде составляем полную систему уравнений состояния цепи по законам Кирхгофа для расчета токов всех ветвей и напряжения на источнике тока.
Схема содержит NУ 4 узла и NB 6 ветвей. Следовательно, по первому закону Кирхгофа можно составить: NУ 1 4 1 3 независимых уравнения, а по второму закону Кирхгофа: NB NУ 1 6 4 1 3 неза-
висимых уравнения.На схеме рис.6 пунктирной линией показано направление обхода контуров.
Узел b: I1 I4 J Узел c: I2 I4 I3 0 Узел а: I3 I1 I5 0
Контур 1: U J I5 2R E1
Контур 2: I2 R I3 R2 I5 2R E2
Контур 3: I2 R I4 R U J E2
61
|
|
|
|
b |
|
|
|
I1 |
|
|
|
|
E1 |
J1к |
J |
UJ |
I |
|
|
|
|||
|
|
|
1к |
|
4 |
J3к |
|
|
|
|
|
a |
|
|
d |
|
|
|
I5 |
2 R |
E2 |
|
R |
|
|
|
|
||
|
|
|
|
|
|
|
|
J2к |
|
d |
|
|
|
|
|
|
|
|
|
|
R |
|
3к |
I 3 |
2к |
I2 |
R/2 c
Рис.6. Расчетная схема
Спомощью программы MATCHAD производим расчет уравнений
вматричной форме:
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
1.009 |
||||
|
|
0 |
1 |
1 |
1 |
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.155 |
|||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
||||||
a |
|
0 |
1 |
0 |
0 |
b |
|
0 |
|
i a 1 b |
i |
|
0.164 |
|||||
|
0 |
0 |
0 |
0 |
220 |
1 |
|
|
100 |
|
0.991 |
|
||||||
|
|
|
||||||||||||||||
|
|
0 |
110 55 |
0 |
220 |
0 |
|
|
|
50 |
|
|
|
|
0.845 |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
0 |
110 |
0 |
110 |
0 |
1 |
|
|
50 |
|
|
|
286 |
|
||||
Значение токов ветвей схемы и напряжение на источнике тока:
I1 1.009 A, I2 1.155 A, I3 0.164 A, I4 0.991 A,
I5 0.845 A, U J 286 B
5. Методом контурных токов определяем токи в ветвях. Выбираем независимые контуры. В рассматриваемой схеме их три
(рис.6). При этом, поскольку ветвь bdсодержит идеальный источник тока, эта ветвь может входить только в один контур. Ток этого контура равен току источника: J2k J 2 A .
Для остальных контурных токов составляем уравнения:
62

J2к (2R R R2 ) J1к 2R J3к R2 E2
J3к (R R2 ) J1к 0 J2к R2 E1
После переноса в правую часть постоянных коэффициентов уравнения примут вид:
J2к (2R R R2 ) J3к R2 E2 J 2R
J2к R2 J3к (R R2 ) E1
Численно получим:
385J2к 55J3к 390
55J2к 165J3к 100
В матричной форме уравнения будут иметь вид:
|
385 |
55 |
|
J2к |
390 |
|
|
|
55 |
|
|
|
|
|
|
|
165 |
|
J3к |
|
100 |
|
|
После расчета получим: |
|
||||||
J2k 1.155 |
A; J3k |
0.991 A. |
|||||
Определяем токи ветвей: |
|
||||||
I1 J1k J3k 2 0.991 1.009 A ; I2 J2k 1.155 A ;
I3 J2k J3k 1.155 0.991 0.164 A ; I4 J3k 0.991 A ;
I5 J1k J2k 2 1.155 0.845 A .
Согласно второму закону Кирхгофа,
U J I5 R I1 0 E1 ,
Отсюда
U J I5 R E1 0.845 220 100 286 B .
6. Определим токи в ветвях схемы методом узловых потенциалов. Между узлами a и b включена ветвь с идеальным источником ЭДС без сопротивления. Поэтому в качестве базисного ( 0 ) удобно принять
узел а, тогда a 0 ; b E1 100 B .
Для узлов c и d составляем узловые уравнения:
63

|
|
1 |
|
1 |
|
|
2 |
|
|
|
1 |
|
1 |
|
|
|
E |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
c |
|
|
|
|
R |
|
|
|
|
|
d |
|
R |
b |
|
R |
R |
|||||||
|
|
R |
|
|
|
R |
|
|
|
|
|
|
|||||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
E2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
c |
|
|
|
d |
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
R |
|
|
R |
|
|
2R |
|
|
|
|
|
R |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Перенеся слагаемое b R1 в правую часть уравнения и подставив известные числовые значения, получаем:
|
|
1 |
|
1 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
50 |
|
|
100 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
c |
|
|
|
|
110 |
|
|
110 |
|
|
d |
110 |
|
110 |
|
|
110 |
||||||||||
|
|
110 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
50 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
c |
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
110 |
|
|
110 |
|
220 |
|
|
|
|
110 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
В матричной форме уравнения будут иметь вид:
|
0.03636 |
0.00909 |
|
|
|
|
1.3636 |
|
|
0.00909 |
|
|
|
c |
|
2.4545 |
|
|
0.0136363 |
|
d |
|
|
|||
После расчета получим:
c 9 B, d 186 B
Токи в ветвях схемы определятся по обобщенному закону Ома:
|
I |
2 |
d c |
|
E2 186 9 50 1.154 A |
||||||||||
|
|
|
|
|
R |
110 |
|||||||||
|
|
|
|
|
|
|
|||||||||
|
I |
|
|
|
2 c |
|
|
2( 9) |
0.163 A |
||||||
|
3 |
|
|
|
|
||||||||||
|
|
|
|
R |
|
|
110 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
I |
|
|
b |
c |
|
|
100 9 |
0.991 A |
|||||||
4 |
|
|
|
|
|
||||||||||
|
|
|
|
R |
|
|
110 |
|
|||||||
|
|
|
|
|
|
|
|
||||||||
I |
|
|
d |
186 |
0.845 A |
||||||||||
5 |
|
|
|||||||||||||
|
|
|
|
2R |
220 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
U J |
|
b |
d |
100 186 286 В |
|||||||||||
Ветвь аb содержит только одну ЭДС E1 и проводимость этой ветви |
|||||||||||||||
равна , поэтому ток I1 невозможно определить через потенциалы узлов. Для узлаа составим уравнение по первому закону Кирхгофа:
I1 I3 I5 0.163 0.845 1.008 A .
7. Составляем уравнение баланса мощности. Мощность источников:
Pи E1I1 E2 I2 U J J 100( 1.009) 50( 1.155) 286 2 413.35 Вт
Мощность потребителей:
64

Pn I22 R I32 R2 I42 R I52 2R
( 1.155)2 110 ( 0.164)2 55 0.9912 110 0.8452 220 413.336 Вт
Погрешность расчета (небаланс) составила
|
|
Pи Pп |
|
|
413.36 413.336 |
|
|
|
|
|
|
100% |
|
|
100% 0,0058% . |
||
|
Pи |
413.36 |
||||||
|
|
|
|
|
|
|||
Таким образом, небаланс в пределах допуска ( ≤ 1 %). |
||||||||
8. |
Определим ток I5 в ветви с сопротивлением 2R методом экви- |
|||||||
валентного генератора.
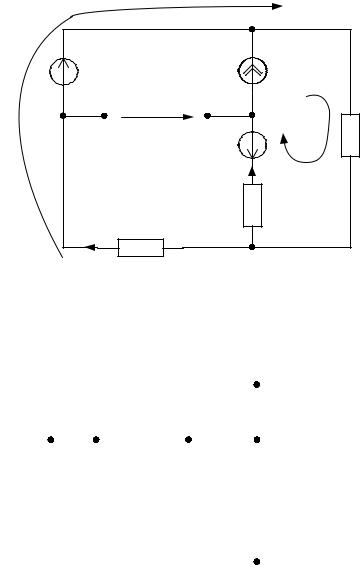
Изобразим схему относительно ветви ad в виде эквивалентного генератора в режиме холостого хода (рис.7).
Из схемы рис.7 определим ЭДС эквивалентного генератора
ЕГ U XX .
|
Согласно второму закону Кирхгофа, U |
|
JR I |
|
|
R |
E |
, |
|||||||||||||||||||||
|
XX |
3ХХ |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
откуда: E |
|
U |
|
|
E |
|
JR I |
|
|
|
R |
|
|
|
|
|
|
|
|
|||||||||
|
Г |
XX |
2 |
3ХХ |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Для определения тока I3ХХ воспользуемся методом контурных то- |
||||||||||||||||||||||||||||
ков: |
J |
|
J 2 A, |
J |
|
|
(R |
R |
) J |
|
|
R E |
|
|
|
|
|
|
|
||||||||||
1K |
2 K |
|
1K |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя численные значения, получим: |
|
|
|
|
|
|||||||||||||||||||||||
|
I3 ХХ |
J2 К |
|
|
E1 J1К R |
|
110 2 110 |
0.727 А, тогда |
|
|
|||||||||||||||||||
|
|
R |
R 2 |
|
110 55 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
EГ U ХХ 50 2 110 0.727 55 310 В
65
|
|
b |
|
J2к |
|
|
|
|
|
|
|
E1 |
|
J |
|
|
|
a |
U xx |
|
d |
|
|
|
|
J1к |
|
||
|
|
E2 |
|
R |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
J |
|
|
R
I 3 xx R/2
c
Рис.7. Эквивалентный генератор в режиме холостого хода
Для определения RГ рисуем вспомогательную схему (рис.8), в которой источники ЭДС замкнуты, а источники тока разомкнуты.
|
|
|
|
|
|
b |
|
|||
|
|
|
|
|
|
|
|
|
||
a |
|
|
R Г |
|
|
|
d |
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|||
|
|
|
|
|
||||||
Рис.8. К определению сопротивления эквивалентного генератора
Из расчета схемы получаем:
|
R |
R |
|
|
|
|
||
|
|
|
|
|
|
110 55 |
|
|
R R |
2 |
|
|
110 |
146.66 Ом . |
|||
|
|
|
|
|
||||
Г |
R |
|
R |
|
|
110 55 |
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|||
По формуле Тевенена-Гельмгольца определяем ток в сопротивлении нагрузки:
I5 |
|
|
EГ |
|
|
310 |
0.845 A |
RГ |
|
|
146.66 220 |
||||
|
|
2R |
|
||||
66
Ток короткого замыкания эквивалентного генератора определится |
|||||||||||
как |
|
|
|
|
|
|
|
|
|
|
|
I |
КЗ |
EГ |
|
310 |
2.113 A . |
|
|
|
|
|
|
|
RГ |
146.66 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
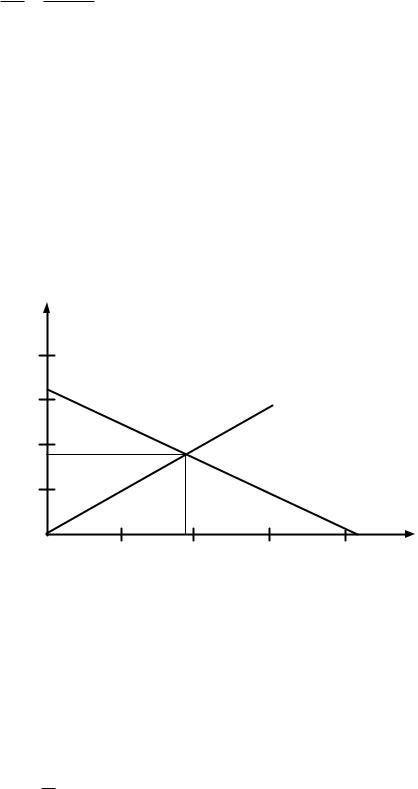
Определим ток I5 графически. Для этого построим в одних осях |
|||||||||||
внешнюю характеристику эквивалентного генератора и вольтамперную |
|||||||||||
характеристику нагрузки (сопротивления 2R ). Внешняя характеристика |
|||||||||||
является линейной и пересекает оси координат в точках U XX и I |
кз |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Вольтамперная характеристика нагрузки также линейна и строит- |
|||||||||||
ся по закону Ома: U5 I5 2R . При этом достаточно задать два значения |
|||||||||||
тока, например I5 0 |
и I5 1А . |
|
|
|
|
|
|
||||
Точка пересечения характеристик будет рабочей точкой генерато- |
|||||||||||
ра, нагруженного на сопротивление 2R , а ее проекция на оси координат |
|||||||||||
– искомыми током и напряжением (рис.9). Получаем графические зна- |
|||||||||||
чения |
U5 186 В, |
I5 0.85 А. |
|
|
|
|
|
|
|||
|
|
|
B |
U |
|
|
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
|
|
|
|
|
U хх |
|
|
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
U5 |
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I5 |
|
|
I кз |
I |
|
|
|
|
|
0 |
|
0.5 |
1 |
1.5 |
2 |
A |
|
|
|
|
|
|
Рис.9. Графическое определение тока и |
|
|
|
||||
|
|
|
|
|
напряжения на сопротивлении 2R |
|
|
|
|||
9. Построим потенциальную диаграмму для контура add′c(рис.6), не содержащего источника тока.
Принимаем a 0
Тогда d a I5 2R 0 0.845 220 185.9 Bd d E2 185.9 50 135.9 B
c d I2 R 135.9 1.155 110 8.85 B
a c I3 R2 8.85 0.164 55 0 B
67
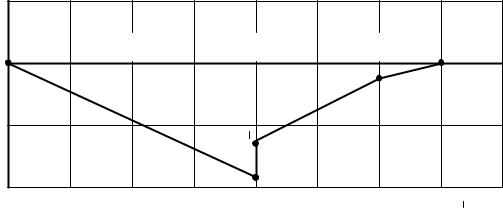
Диаграмма приведена на рис.10. |
|
|
|
|||
B |
|
|
|
|
|
|
0 |
a |
110 |
220 |
330 |
a |
R |
|
|
|
||||
|
|
|
|
|
Ом |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
-100 |
|
|
|
|
|
|
|
|
|
d |
|
|
|
-200 |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
Рис.10. Потенциальная диаграмма для контура a d d c a |
|||||
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАСЧЕТНОГРАФИЧЕСКОЙ РАБОТЫ №2
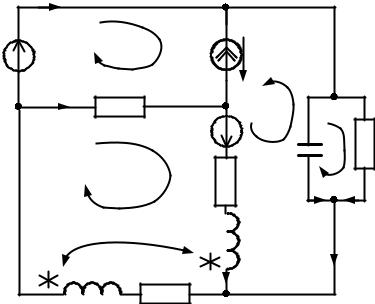
1.Изобразим схему электрической цепи для условного варианта, рассмотренного в методических указаниях к заданию №1 (рис.11).
2.В общем (буквенном) виде составляем полную систему уравнений состояния цепи по законам Кирхгофа для расчета токов всех ветвей
инапряжения на источнике тока.
Схема содержит NУ 4 узла и NB 7 ветвей. Следовательно, по первому закону Кирхгофа можно составить NУ 1 4 1 3 независимых уравнения, а по второму закону Кирхгофа NB NУ 1 7 4 1 4 независимых уравнения.
В индуктивных элементах токи i2 (t), i3 (t) ориентированы одинаковым
образом относительно одноименных зажимов, обозначенных звѐздочками, поэтому имеем вариант согласного включения.
Узел а: |
i3 i1 |
i5 0 |
Узел b: i1 iR 4 iC 4 |
J |
|
Узел d: |
i5 i2 J |
|
Контур 1:U J |
i5 2R e1 |
|
Контур 2: i 2R i R L |
di2 |
M |
di3 |
|
i |
R |
L |
di3 |
M |
di2 |
e |
||||||||||
|
|
|
|
|
|
|
|||||||||||||||
5 |
|
2 |
|
|
dt |
|
|
|
dt |
|
3 |
2 |
|
dt |
|
dt |
2 |
||||
Контур 3: |
i R L |
di2 |
M |
di3 |
|
1 |
|
i |
|
dt u |
|
e |
|
||||||||
|
|
C |
|
J |
|
||||||||||||||||
|
2 |
|
dt |
|
|
|
dt |
|
|
C 4 |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
68
|
C |
|
|
|
|
Контур 4: |
1 |
|
i |
dt i |
R 0 |
|
|
||||
|
|
|
C 4 |
R4 |
|
b
i1 (t) |
|
|
|
|
|
|
e1(t) |
1к |
J(t) |
|
u (t) |
|
|
|
|
|
|
|||
|
|
|
|
J |
|
|
|
2R |
|
d |
|
|
|
a |
|
|
3к |
|
|
|
i5(t) |
|
|
|
|
|
|
|
e (t) |
|
|
|
|
|
|
|
2 |
|
C |
4к |
R |
|
|
|
|
 i3(t) 2к R
i3(t) 2к R
|
M |
|
iC4(t) iR4(t) |
|||
|
L |
|
|
|
||
|
|
|
i4 |
(t) |
||
L |
R/2 |
i2(t) |
||||
|
|
|||||
c
Рис.11. Схема электрической цепи переменного тока
2.Определим реактивные сопротивления:
ХL L 314 0.35 110 Oм; Х М М 314 0.185 55 Ом;
Х |
|
|
1 |
|
1 |
110 Ом. |
С |
|
314 28.95 10 6 |
||||
|
|
С |
|
|||
|
|
|
|
|||
Здесь и далее 2 f 2 314 50 314 рад с – угловая частота
с – угловая частота
источников ЭДС и тока. |
|
|
|
|
|
||||||||||
|
|
3. Полные сопротивления ветвей схемы: |
|
||||||||||||
Z1 0; |
|
|
|
|
|
|
|
|
|
||||||
Z 2 R jX L 110 j110 Oм; |
|
|
|
|
|||||||||||
Z |
|
|
R |
jX |
|
55 j110 Oм; |
|
|
|
|
|||||
3 |
|
L |
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Z |
|
|
|
R ( jXC ) |
R jX |
|
|
110 ( j110) |
55 j55 Oм; |
||||
|
|
4 |
|
C 4 |
|
||||||||||
|
|
|
|
|
|
|
4 |
|
|
j110 |
|
||||
|
|
|
|
|
|
|
R jXC |
|
110 |
|
|||||
Z 5 2R 220 Ом.
Комплексы действующих значений ЭДС и тока источников:
E1 100e j900 0 j100 B;
|
50e |
j 450 |
35.35 j35.35 B; |
|
2e |
j300 |
1.732 |
j1 A. |
E2 |
|
J |
|
69
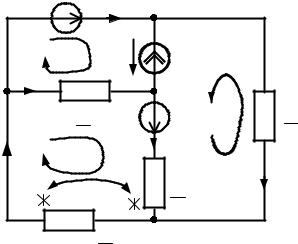
Расчетная схема с комплексными источниками ЭДС и тока и комплексными сопротивлениями ветвей показана на рис.12.
. |
|
. |
|
|
|
|
|
|
|
|
E1 |
|
I1 |
|
|
b |
|
|
|
|
|
|
|
. |
|
|
|
. |
|
|
|
|
|
1к |
U |
|
|
|
|
|
|
||
|
|
|
|
J |
|
|
|
|
||
|
|
J |
|
|
|
|
|
|
|
|
a . |
|
|
|
|
d |
. |
|
|
|
|
I5 |
|
Z5 |
|
|
|
|
3к |
|
Z 4 |
|
|
. |
|
|
E |
2 |
|
||||
. |
|
|
I |
2 |
. |
|
|
|
|
|
I3 |
2 к |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
I. |
|
|||
|
|
M |
|
|
|
Z |
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 3 |
|
|
c |
|
|
|
|
|
Рис.12. Расчетная комплексная схема |
||||||||||
|
замещения электрической цепи |
|||||||||
4. Составляем систему уравнений в комплексной форме по законам Кирхгофа для расчета токов ветвей и напряжения на источнике тока:
Узел b: |
|
|
I |
I |
J |
|
|
|
|
|
||
|
|
|
1 |
4 |
|
|
|
|
|
|
|
|
Узел c: |
|
|
I |
I |
I |
0 |
|
|
|
|
||
|
|
|
2 |
4 |
|
3 |
|
|
|
|
|
|
Узел а: |
|
|
I |
I |
I |
0 |
|
|
|
|
||
Контур 1: |
|
3 |
1 |
|
5 |
|
|
|
|
|
|
|
|
UJ I5 2R E1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
I2 jXM I5 Z 5 |
E2 |
|||
Контур 2: |
|
I2 Z 2 I3 jXM |
I3 Z3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
E2 |
|
|
Контур 3: |
|
I2 Z 2 I3 jXM |
I4 Z 4 |
UJ |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя численные значения, получим: |
|
|
||||||||||
Узел b: |
I I J |
|
|
|
|
|
|
|
|
|
||
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
Узел c: |
I |
I |
I |
0 |
|
|
|
|
|
|
|
|
|
2 |
4 |
3 |
|
|
|
|
|
|
|
|
|
Узел а: |
I |
I |
I |
0 |
|
|
|
|
|
|
|
|
Контур 1: |
3 |
1 |
5 |
|
|
|
|
|
|
|
|
|
UJ |
I5 220 j100 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Контур 2: |
I (110 j165) I |
(55 j165) I 220 35.35 j35.35 |
||||||||||
|
2 |
|
|
|
3 |
|
|
|
5 |
|
35.35 j35.35 |
|
Контур 3: I2 (110 j110) I3 j55 I4 (55 j55) UJ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Спомощью программы MATCHAD производим расчет уравнений
вматричной форме:
|
1 |
0 |
0 |
1 |
|
0 |
0 |
|
|
1.732 i |
|
||
|
|
|
|
|
|
||||||||
|
0 |
1 |
1 |
1 |
|
0 0 |
|
0 |
|||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
a |
1 |
0 |
1 |
0 |
|
1 |
0 |
b |
|||||
|
|
100i |
|
||||||||||
|
0 |
0 |
0 |
0 |
220 |
1 |
|
|
|||||
|
|
|
35.35 35.35i |
||||||||||
|
|
0 |
110 165i |
55 165i |
0 |
70 |
220 |
0 |
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
35.35 35.35i |
||||
|
0 |
110 110i |
55i |
55 |
55i 0 |
1 |
|
||||||
|
|
|
|
|
|||||||||
