
ТОЭ / ТОЭ ТПУ
.pdf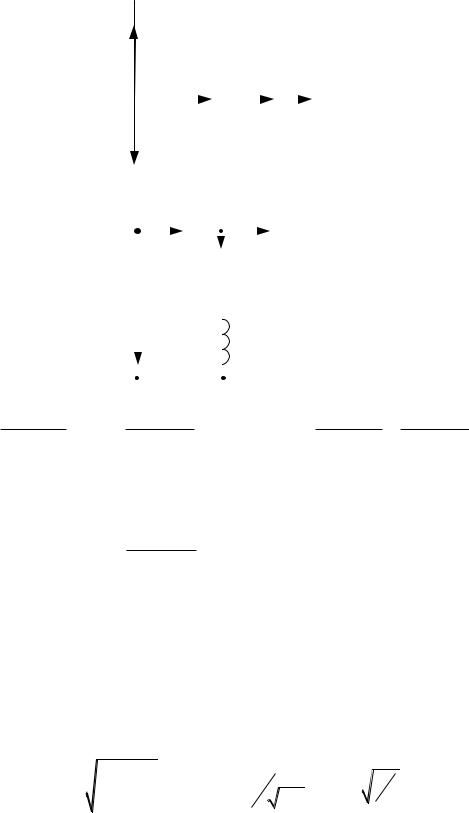
Векторная диаграмма при резонансе токов
+j 
I.C |
|
|
|
|
. . |
. |
|
||
|
I |
I R |
U |
|
I.L |
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
Резонанс токов в параллельном контуре с потерями |
||||||||||
|
|
I. |
. |
|
|
|
|
|
||
|
|
|
IC |
|||||||
|
|
|
|
|
I.L |
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
R1 |
|
|
R2 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
U |
|
|
|
|
|
|
|
|
|
|
jX L |
|
-jX C |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y1 R1 1jX L ; Y 2 R2 1jXC ; Y Y1 Y 2 R1 1jX L R2 1jXC
По условию резонанса мнимая часть полной проводимости цепи должна равняться нулю. Чтобы выделить мнимую часть умножим числитель и знаменатель на комплексно сопряженные числа:
R1 jX L
R2 |
X 2 |
|
||
1 |
|
|
L |
|
j |
|
|
X C |
|
|
|
|
||
2 |
2 |
|||
|
|
R2 |
X C |
|
|
|
R1 |
|
|
|
|
|
2 |
|
2 |
|
|
R1 |
X L |
|
|
X L |
|
|
|
. |
|
2 |
2 |
||
|
R1 |
X L |
|
|
|
R2 |
|
|
|
|
|
|
|
||
2 |
|
2 |
|||
|
R2 |
X C |
|
|
Приравняв к нулю мнимую часть, находим условие резонанса в параллельном контуре с потерями:
|
XC |
|
|
X L |
|
|
|
|
|
. |
|
R2 |
X 2 |
R2 |
X 2 |
||
2 |
C |
1 |
L |
||
Из этого выражения находим резонансную частоту:
|
|
2 |
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
; |
L |
|
|||
|
1 |
|
, где |
|
. |
||||||
|
|
|
|
||||||||
р 0 |
2 |
R22 |
|
|
0 |
|
LC |
|
C |
|
|
31
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ue |
j 0 |
, |
токи в |
параллельных ветвях |
U |
ILа |
jILр ; |
|||||
При U |
|
IL |
jX L |
||||||||||
|
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
U |
|
I |
|
jI |
|
. |
|
|
|
|
|
|
|
Cа |
Cр |
|
|
|
|
|
|||||
C |
R2 |
jXC |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
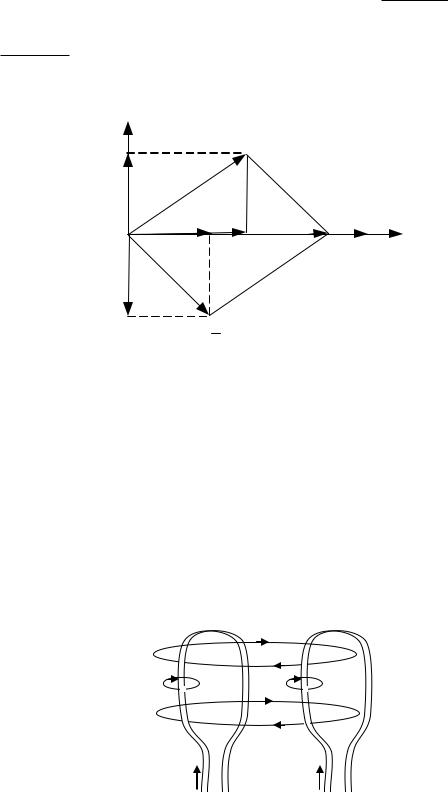
Векторная диаграмма |
|
|
|
|
|
|
|
|
|
|
+j |
|
|
. |
|
|
|
|
|
|
|
|
|
|
I.C р |
|
|
IC |
|
|
|
|
|
|
|
|
|
|
|
|
. . |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
I |
U |
|
|
|
|
|
|
|
|
. |
|
|
. |
. |
+1 |
|
|
|
|
|
|
|
|
I Lр |
|
I L а |
IC а |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
IL |
|
|
|
|
|
|
|
ТЕМА 4.ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С |
||||||||||
|
|
|
|
|
ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ |
|
|
||||||
При наличии в цепи катушек, взаимодействующих своими магнитными потоками, цепь называют индуктивно связанной или цепью с взаимной индуктивностью.В общем случае любое число катушек может иметь индуктивную связь.
Магнитный поток Ф1, Вб (Вебер)первого контура (создается i1 ) частично замыкается вокруг витков первого контура, создавая поток рассеяния Ф11 , и частично проходит через витки второго контура, создавая поток взаимной индукции) Ф21 : Ф1 Ф11 Ф21 .
Ф21 |
|
Ф11 |
Ф22 |
|
Ф12 |
i1 |
i2 |
Магнитный поток Ф2 второго контура (создается i2 ) частично замыкается вокруг витков второго контура, создавая поток рассеяния Ф22 , и
32
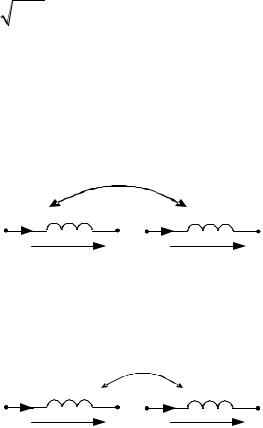
частично проходит через витки первого контура, создавая поток взаимной индукции Ф12 : Ф2 Ф22 Ф12 .
Потокосцепление первого контура:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 w1 (Ф1 Ф12 ), |
потокосцепление второго контура: |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 w2 (Ф2 Ф21 ) , где |
|
w1 , |
w2 – число витков первого и второго контуров. |
||||||||||||||||
L |
w1Ф11 |
; |
L |
w2Ф22 |
, Гн – собственные индуктивности контуров; |
||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||
1 |
|
|
|
i1 |
2 |
|
|
|
i2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
М |
|
|
w1Ф12 |
|
; М |
|
|
w2Ф21 |
|
, Гн – взаимные индуктивности. |
|||||||
12 |
|
21 |
|
|
|||||||||||||
i2 |
|
i1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Для линейных цепей Ф21 Ф12 ; M12 M 21 M . |
||||||||||||||
|
|
|
Степень магнитной связи двух катушек характеризуется коэффи- |
||||||||||||||
циентом связи k |
|
M |
|
|
. Начала обмоток называются одноимѐнными |
||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||
|
L1L2 |
|
|||||||||||||||
зажимами и обозначаются на схеме звездочками или точками. Направление магнитного потока в катушке индуктивности опре-
деляется по правилу буравчика, поэтому, если потоки взаимной индукции Ф21 и Ф12 совпадают по направлению, то такое включение называ-
ют согласным включением. При этом токи направлены одинаковым образом относительно одноименных зажимов:
M
i1 * |
L1 |
i2 * |
L 2 |
|
u1 |
|
u2 |
При встречном включении взаимные магнитные потоки Ф21 и Ф12 на-
правлены навстречу друг другу. При этом токи направлены различным образом относительно одноименных зажимов:
M
i1 |
L1 * |
i2 * |
L2 |
|
u1 |
|
u2 |
Мгновенное значение напряжения на индуктивно связанных ка-
тушках:
33
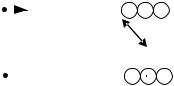
u w |
d(Ф11 Ф12 ) |
L |
di1 |
M |
di2 |
; |
u w |
d (Ф22 Ф21) |
L |
di2 |
M |
di1 |
, |
|
|
|
|
|
|
||||||||
1 1 |
dt |
1 dt |
|
dt |
|
2 2 |
dt |
2 |
dt |
|
dt |
|
|
знак «+» берется при согласном включении катушек, а «–» – при встречном включении.
U1 |
Комплексы действующих значений напряжений на катушках |
|||||||||
UL1 |
UМ1 |
jXL1I1 jXМ I2 ; |
U2 |
UL2 UМ 2 |
jXL2I2 |
jXМ I1 , |
||||
|
|
|
|
|
|
|
|
|
|
|
где X L1 L1 |
; X L 2 L2 ; |
X М M , Ом – |
реактивное |
сопротивление |
||||||
индуктивной связи; UМ1 jXМ I2 |
, UМ 2 jXМ I1 – комплексные напряже- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
ния взаимной индукции. |
|
|
|
|
|
|
|
|||
|
При согласном включении берется знак «+» и вектора UМ1 и UМ 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
опережают свои токи I2 |
и I1 на 900 (индуктивный характер), а при |
|||||||||
встречном включении берется знак «–», и вектора UМ1 |
и UМ 2 |
отстают |
||||||||
|
|
|
|
|
|
|
|
|
|
|
от своих токов на 900 (емкостной характер). |
|
|
|
j MI |
||||||
При расчете цепи по уравнениям Кирхгофа напряжение UM |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
учитывается наравне с другими падениями напряжения с учетом вида включения (согласное или встречное).
Последовательное соединение двух индуктивно связанных катушек
|
|
|
|
|
|
|
. |
R1 |
|
|
|
|
|
XL1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
XM |
|
|
|
|
|
||||
|
|
|
|
|
|
|
U |
R 2 |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
По |
закону |
Ома: |
UR1 IR1 ; |
UR2 |
IR2 |
; Напряжения на катушках: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UM . |
|||
U1 |
jXL1I jXM I UL1 |
UM |
; U2 |
jXL2 I jXM I UL2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Входное сопротивление цепи Z R1 R2 j( X L1 X L 2 |
2 X M ) . |
|||||||||||||||||||||
|
|
|
U |
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий ток |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
||||
|
|
R j( X |
|
|
X |
|
2X |
|
|
|
|
|
||||||||||
|
|
|
Z R |
L1 |
L2 |
M |
) |
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
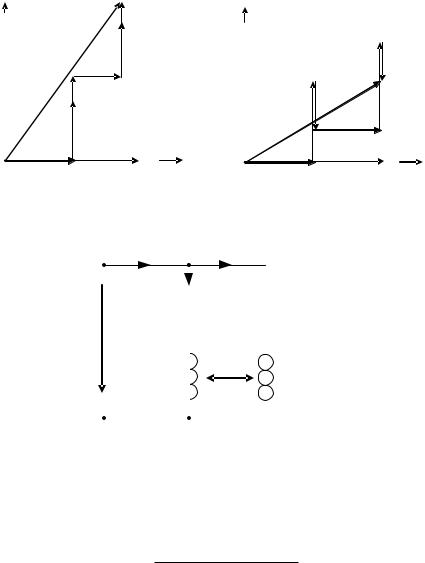
«+» – при согласном включении;«–» – при встречном.
При неизменном действующем значении входного напряжения больший по величине ток будет при встречном включении.
Векторные диаграммы
34
.
|
|
|
UM |
|
|
|
|
|
|
+j |
|
|
|
+j |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
. |
. |
UL2 |
|
|
|
|
. |
|
|
|
|
|
|
|
UM |
|||
|
|
|
|
|
|
|
. |
||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
. |
|
|
|
. |
|
|
. |
UL2 |
|||
|
|
|
|
|
|
|
|
|
|
|
. |
|
. |
|
|
. |
. |
. |
|
|
|
I |
+1 |
|
|||||
|
|
|
|
|
+1 |
||||
|
|
|
|
|
|
|
|
||
|
согласное включение |
|
|
встречное включение |
|
||||
Параллельное соединение двух индуктивно связанных катушек |
||||||||||
|
|
|
I. |
|
I.2 |
|
|
|||
|
|
|
I.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
R1 |
|
|
|
|
|
|
R 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|||
|
|
|
|
XM |
|
|
|
XL2 |
||
|
|
|
XL1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Уравнения по законам Кирхгофа в комплексной форме с учетом влияния индуктивной связи:
I I1 |
I2 ; |
U I1R1 |
jX L1I1 |
jXM I2 |
; U I2R2 |
jXL2I2 |
jXM I1 . |
|||
|
|
|
|
|
|
|
|
|
|
|
Совместное решение уравнений позволяет определить ток:
I U Z1 Z 2 2( jX M ) ,
Z1 Z 2 X M2
где Z1 R1 jX L1 ;. Z 2 R2 jX L 2 ., при этом знак «+» берется при со-
гласном включении катушек,а «–» – при встречном.
При неизменном входном напряжении больший ток будет при встречном включении.
Потребляемая реактивная мощность с учетом индуктивной связи катушек определяется по формуле
Qп Ii2 X Li |
Ik2 XCk 2X M Id Ir cos( d r ) , где |
i |
k |
слагаемое 2 X M Id Ir cos( d r ) учитывает индуктивную связь; знак «+» ставится при согласном включении катушек и «–» при встречном; Id , Ir – действующие значения токов индуктивно связанных катушек; d , r – их начальные фазы.
35
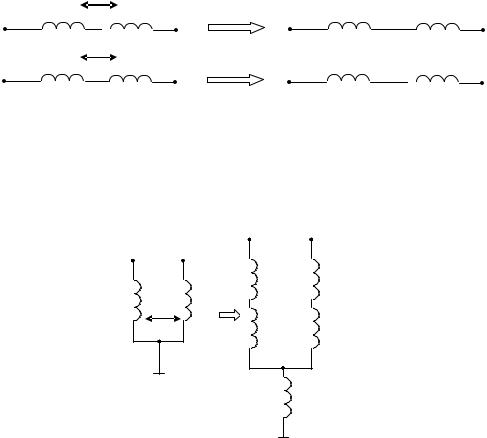
Развязка индуктивной связи
Используется с целью упрощения расчетов. После развязки схема может быть рассчитана любым методом в комплексной форме.
Развязка последовательно соединенных катушек:
jXL1 |
XM |
j(XL1 XM ) |
j(XL2 XM ) |
jXL2 |
|||
* |
* |
|
|
jXL1 |
XM |
j(XL1 XM ) |
j(XL2 XM ) |
jXL2 |
|||
* |
|
* |
|
Развязка индуктивных связей катушек, имеющих общий узел:
если катушки подключены к общему узлу одноименными зажимами, то в эквивалентной схеме без индуктивной связи последовательно к каждому из них подключается сопротивление jX M , а в общую ветвь со-
противление jX M :
jXL1 |
jXL2 |
jXL1 |
jXL2 |
1 |
|
|
|
XM |
|
|
|
* |
* |
jXM |
jXM |
jXM
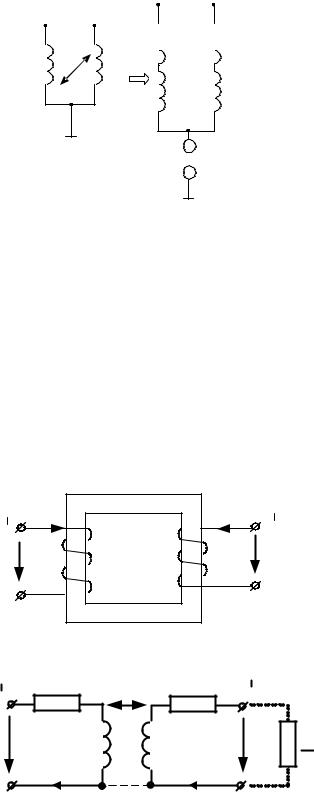
если катушки подключены к общему узлу разноименными зажимами, то в эквивалентной схеме без индуктивной связи последовательно к каждому элементу подключается сопротивление jX M , а в общую ветвь
сопротивление jX M :
36
jXL1 * jXL 2  jXL1
jXL1  jXL2
jXL2
* XM |
jXM jXM |
 jXM
jXM
ТЕМА 5. ДВУХОБМОТОЧНЫЙ ТРАНСФОРМАТОР В ЛИНЕЙНОМ РЕЖИМЕ
Трансформатор предназначен для преобразования величин переменных токов и напряжений при неизменной частоте. В простейшем случае он представляет собой две обмотки на замкнутом сердечнике из ферромагнитного материала. Передача энергии из первичной во вторичную обмоткупроисходит благодаря явлению взаимной индукции. Обмотка 1-11 называется первичной и подключается к источнику электроэнергии с напряжением u1 , обмотка 2-21 называется вторичной и
подключается к нагрузке с напряжением u2 .
1 |
i1 |
|
|
i2 |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
u1 |
w1 |
w2 |
|
u2 |
1 |
|
|
|
|
2 |
Схема замещения линейного трансформатора:
1 |
R1 |
XM |
R2 |
2 |
|
|
|
|
|
|
|
|
|
. |
* |
* |
|
|
. |
|
. XL1 |
|
XL2 |
|
Z н |
||
U1 |
|
. |
U2 |
|||
|
I1 |
|
|
|
|
|
|
|
|
I2 |
|
|
|
1 |
а |
|
а |
|
2 |
|
|
|
|
|
|
|
|
Уравнения трансформатора в линейном режиме:
37
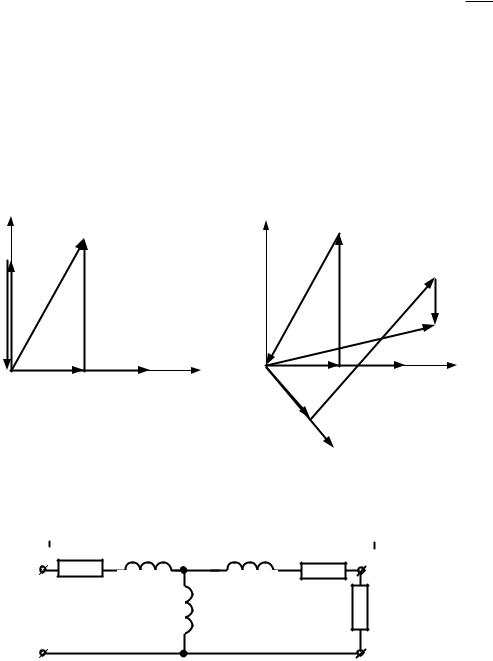
U1 |
I1R1 I1 jX L1 |
I2 jX M |
|||
|
|
|
|
|
|
UR1 |
UL1 |
UM 1 |
|
|
|
|
|
|
|
|
|
0 U |
2 I2 R2 I2 |
jX L2 |
I1 jX M |
||
|
|
|
|
|
|
U2 |
UR 2 U L2 UM 2 |
|
|||
|
|
|
|
|
|
где U2 I2 Z н I2 (Rн jXн )- напряжение на нагрузке.
Коэффициент трансформации – это отношение напряжения на зажимах обмотки высшего напряжения (вн) к напряжению на зажимах
U х
обмотки низшего напряжения (нн) в режиме холостого хода: kтр вн .
Uннх
Если U |
|
U |
|
и R |
X |
|
, то k |
|
|
w1 |
, где |
w |
, w – числа витков первич- |
1 |
2 |
L1 |
тр |
|
|||||||||
|
|
1 |
|
|
|
w2 |
1 |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
ной и вторичной обмоток. Если в режиме холостого хода |
|||||||||||||
( Z н , I 2 0 ) U1 |
U2 , |
kтр 1, то трансформатор называют понижаю- |
|||||||||||
щим, если U1 U2 , kтр 1– повышающим. |
|
|
|||||||||||
Диаграммы работы трансформатора в режиме холостого ходаи короткого замыкания:
+j |
|
|
|
|
. |
|
|
|
U1 |
|
|
. . |
. |
|
|
UM2 |
U2 |
UL1 |
|
|
. |
. |
|
|
UR1 |
I1 |
+1 |
+j |
|
|
|
. |
|
|
|
UM2 |
. |
|
|
|
|
|
|
|
. |
UL1 . |
|
|
|
UM1 |
|
|
UL2 |
|
|
|
|
|
|
|
|
. |
|
|
|
U1 |
|
|
. |
. |
|
. |
UR2 |
I2 |
+1 |
|
|
|
|
UR1 |
. |
|
|
|
|
|
|
|
I1 |
|
|
Эквивалентная схема трансформатора без индуктивной связи
(за общий узел принимается точкаа в схеме замещения с индуктивной связью):
1 |
R1 |
j(XL1 XM ) |
j(XL2 XM ) |
R2 |
2 |
|
|
а |
|
|
|
|
|
|
jXM |
|
ZН |
1 |
|
|
|
|
2 |
|
|
|
|
|
38
ТЕМА 6. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ИСТОЧНИКАМИ НЕСИНУСОИДАЛЬНЫХ ПЕРИОДИЧЕСКИХ НАПРЯЖЕНИЙ И ТОКОВ
Несинусоидальные периодические напряжения и токи возникают в цепях содержащих нелинейные элементы – электроника, автоматика, радиотехника, и т.д.Расчет таких цепей заключается в следующем:
1.Разложение несинусоидальных ЭДС или токов источников тока в ряд Фурье.
2.Расчет электрической цепи по принципу наложения и определение постоянной и гармонических составляющих токов и напряжений в ветвях цепи.
3.Определение мгновенных или действующих значений токов и напряжений.
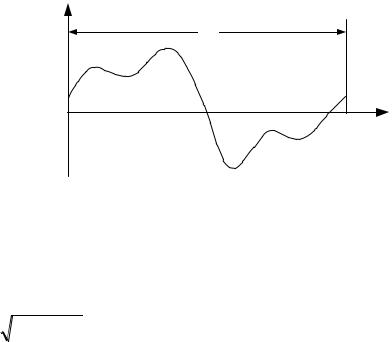
Разложение несинусоидальных ЭДС или токов источников тока в ряд Фурье.
f(t) |
|
|
T |
0 |
t |
Для разложения в ряд Фурье используется следующая форма за-
писи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
Т |
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (t) A0 Akm sin(k t k ),где A0 |
1 |
|
|
f (t)dt |
||||||||||||||||
|
0 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
Ckm |
, |
|
|
|
|
||||||
A |
|
|
B2 |
C2 , |
k |
причем |
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||
km |
|
|
|
km |
km |
|
|
Bkm |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
B |
|
1 |
|
T f (t)sin(k t)dt, C |
|
2 |
|
T |
f (t)cos(к t) dt |
|||||||||||
km |
|
|
|
|
|
|
|
к |
|
T |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
Здесь |
|
|
A0 – постоянная составляющая, |
|
A1m sin( t 1 ) – первая |
|||||||||||||||
(основная) гармоника, ее период |
|
T |
2 |
равен периоду самой функции. |
||||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Все остальные гармоники называются высшими.
39
Так, Akm sin(k t k ) – гармоническая составляющая k-го поряд-
ка, (k-я гармоника), чей период T |
2 |
|
T |
. Каждой гармонике может |
|
|
|||
k |
k |
|
k |
|
|
|
|||
быть сопоставлена ее комплексная амплитуда:
Akm Akme j k Bkm jCkm
Действующие и средние значения несинусоидальных величин
Пусть известно разложение некоторого тока в ряд Фурье: i t I0 ik I0 Ikm sin(k t k ) .
Найдем его действующее (среднеквадратичное) значение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T i2 (t) dt |
|
|
Im21 |
|
Im2 |
|
|
|
|
|
|
|
||
I |
I 2 |
|
|
2 |
... I 2 |
I 2 |
I 2 |
... . |
||||||||
|
|
|
|
|||||||||||||
|
T |
|
0 |
|
2 |
|
2 |
0 |
1 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действующее значение не зависит от начальных фаз гармоник. Его можно измерить приборами электромагнитной и электродинамической систем (а действующее значение напряжения – еще и электростатическими вольтметрами).
Среднее за период значение токаравно постоянной составляю-
1 T
щей в разложении I0 T 0 i(t)dt и может быть измерено приборами магнитоэлектрической системы.
|
|
T |
|
|
|
|
|
|
|
|
1 |
T |
|
|
|
Среднее по модулю значение тока I |
ср |
|
|
i(t) |
dt |
измеряется |
|
|
|
|
|
0 |
|
|
|
магнитоэлектрическими приборами с выпрямителем.
Волновые диаграммы и частотные спектры.
Для примера рассмотрим функцию несинусоидального тока в ви-
де ряда Фурье: i t 1 3sin( t 300 ) 2sin(3 t 900 ) , А
Совокупность комплексных амплитуд Akm всех гармоник данной
функции можно рассматривать как ее дискретный спектр. На графике он может быть представлен в виде линейчатых амплитудно- и фазочастотных спектров, которые показывают зависимость амплитуд гармоник Akm их начальных фаз k от номеров гармоник или их частот k .
40
