
ТОЭ / ТОЭ ТПУ
.pdf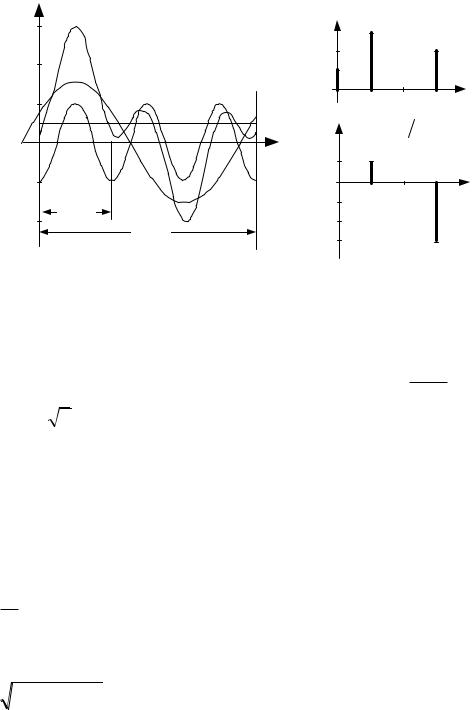
6 |
i |
i |
|
|
A |
Ikm |
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
i1 |
|
|
1 |
|
|
|
|
|
2 |
|
I0 |
|
|
0 |
1 |
2 |
3 |
k |
|
|
|
2π |
ψk |
k |
|
|||
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
θ |
|
|
|
|
|
|
|
i3 |
|
|
|
|
|
|
||
-2 |
|
|
|
6 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
1 |
2 |
|
k |
|
|
|
|
|
|
|
||||
-4 |
|
ωT3 |
|
|
|
|
|
|
|
|
ωT1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
Коэффициенты, характеризующие формунесинусоидальных кривых.
Наиболее часто употребляются следующие коэффициенты: коэффициент амплитуды kA , равный отношению наибольшего
значения функции к ее действующему значению kA Fмакс ; для сину-
F
соиды kA 
 2 1,41.
2 1,41.
коэффициент формы kф , равный отношению действующего зна-
чения функции к среднему по модулю |
k |
|
|
F |
; для синусоиды k |
|
1,11 |
ф |
|
ф |
|||||
|
|
|
Fср |
|
|||
|
|
|
|
|
|
||
.
коэффициент искажения kИ , равный отношению действующего значения первой гармоники к действующему значению самой функции
kИ FF1 ; для синусоиды kИ 1.
коэффициент гармоник kГ , равный отношению действующего значения высших гармоник к действующему значению основной
kГ |
|
F 2 |
F 2 |
... |
|
0 |
|
2 |
3 |
|
; для синусоиды kГ |
||
|
|
F1 |
|
|||
|
|
|
|
|
|
Впромышленной сети напряжение несколько отличается от синусоидального. В стандарте вводят понятие практически синусоидального напряжения,у которого коэффициент искажения не должен превышать 5%.
Мощность в цепи несинусоидального тока.
41
Для напряжения и тока двухполюсника, заданных в виде ряда Фу-
рье: u(t) U0 
 2U1 sin( t 1)
2U1 sin( t 1) 
 2U2 sin(2 t 2 ) ...
2U2 sin(2 t 2 ) ...
i(t) I0 
 2I1 sin( t 1)
2I1 sin( t 1) 
 2I2 sin(2 t 2 ) ...
2I2 sin(2 t 2 ) ...
активная мощность, потребляемая двухполюсником равна:
P P P P ... U |
0 |
I |
0 |
U I cos |
U |
I |
2 |
cos ... , Вт , |
|||||||||||||
0 |
1 |
|
2 |
|
|
|
1 |
1 |
1 |
2 |
|
|
|
2 |
|||||||
где 1 |
1 , 2 |
2 |
2 - сдвиги фаз между гармониками напряжения |
||||||||||||||||||
и тока. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Реактивная |
|
|
|
|
|
|
|
|
мощность |
двухполюсника |
||||||||||
Q Q1 Q2 ... U1I1 sin 1 U2 I2 sin 2 ... , |
вар , причем для постоянной |
||||||||||||||||||||
составляющей Q0 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Полная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мощностьдвухполюсника |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
S UI |
U 2 |
U 2 |
U |
2 |
... |
I 2 |
I 2 |
I 2 |
... , |
ВА |
|||||||||||
|
|
0 |
1 |
2 |
|
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|||
|
в |
большинстве |
|
|
|
случаях |
для |
|
негармонических функций |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
S |
P2 |
Q2 |
. Если S |
|
|
|
P2 Q2 , то формынесинусоидальных напряже- |
||||||||||||||
ния u(t) и тока i(t) одинаковы. |
|
|
|
|
|
|
|
|
|||||||||||||
Коэффициент мощности cos PS 1.
В расчетах часто применяют эквивалентные синусоиды. При этом реальные несинусоидальные кривые заменяются эквивалентными синусоидами с тем же периодом T, теми же действующими значениями
тока и напряжения I,U и таким углом сдвига фаз Э arccos UIP ,
который обеспечил бы ту же самую активную мощность Р.
ТЕМА 7. ТРЕХФАЗНЫЕ ЦЕПИ
Трехфазная цепь – это совокупность трех электрических цепей (фаз), в которых действуют одинаковые ЭДС одной и той же частоты,
сдвинутые друг относительно друга на1200 : |
|
|
|
|
|
|
|
|||||||||||||
e |
A |
E |
m |
sin t ; |
e |
E |
|
sin( t 1200 ) ; |
e E |
sin( t 1200 ) . |
|
|||||||||
|
|
|
B |
m |
|
|
|
|
|
C |
m |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Em |
|
|
|
j1200 |
|
|
|
j1200 |
|
||
В комплексной форме: EA |
|
|
|
|
Eф ; EB |
Eфe |
|
|
; |
EC |
Eфe |
|
. |
|||||||
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Алгебраическая сумма симметричной трехфазной системы равна нулю:
EA EB EC Eф (1 a2 a) Eф (1 0.5 0.866 j 0.5 0.866 j) 0.
42
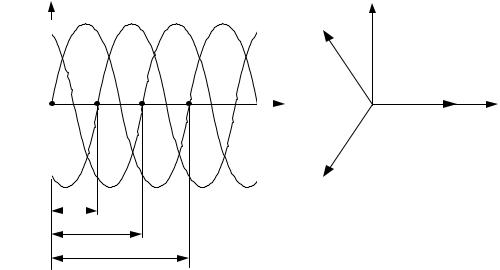
Фазный множитель а – это комплексная величина, которая применяется при расчете трехфазных цепей для упрощения записи: a e j1200 0.5 j0.866; a2 e j 2400 0.5 j0.866; а3 е j3600 1
Таким образом: EA Eф ; EB Eфa2 ; EС Eфа
Система ЭДС (напряжений, токов) называется симметричной, если она состоит из одинаковых по модулю ЭДС (напряжений, токов) одной и той же частоты, но сдвинутых относительно друг друга на1200 .
e |
eA |
eB |
eC |
. |
+j |
|
|
|
|
||||
|
|
|
|
EC |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
EA |
+1 |
|
|
|
|
|
|
|
|
|
|
t |
|
0 |
|
|
|
|
|
. |
|
|
|
|
|
|
EB |
|
|
|
T/3 |
|
|
|
|
|
|
2T/3 |
|
|
|
|
|
|
T |
|
|
|
|
|
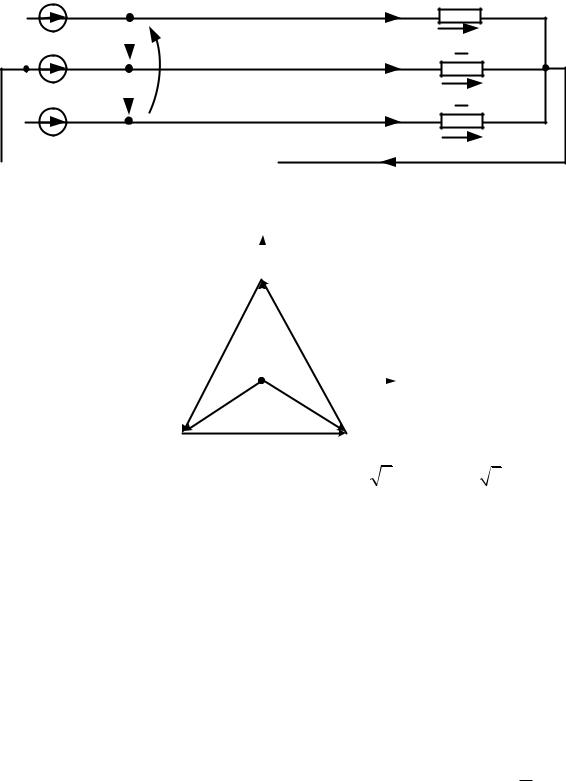
Cоединение « звезда –звезда» с нулевым проводом (Y/Y)
Линейные провода – это провода соединяющие источники с приемниками.
Линейные напряжения – это напряжения между линейными про-
водами (UAB ,UBC ,UCA ). Линейные токи ( IA, IB , IC ) являются одновременно фазными токами и текут от источника к приемнику. Нейтральный провод – это провод, соединяющий нейтральную точку источников Nи нейтральную точку приемников n. Фазные напряжения-
приемника – это напряжения между линией и точкой n( UA ,UB ,UC
).Напряжение смещения нейтрали UN IN Z N показывает смещение точки n по отношению к точке N.
43
|
. |
|
|
|
|
|
|
|
|
. |
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
линейный провод |
IA |
|||
|
|
|
|
|
|
|
|||||
|
|
|
. |
|
|
|
|
||||
|
|
. |
|
|
|
|
. |
|
|
. |
|
|
|
|
|
|
|
|
|||||
|
|
UAB |
|
|
|
|
|
||||
N |
|
EB |
|
В |
U CA линейный провод |
I B |
|||||
|
|
||||||||||
|
|
. |
|
|
|||||||
|
|
. |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
U BC |
|
|
|
|
|
|
|
||
|
|
EC |
|
|
|
|
|
|
|
||
|
|
|
|
С |
|
линейный провод |
I C |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Z N |
I. |
|
|
нейтральный провод |
|
|
|
N |
||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Z A |
|
|
|
. |
|
Z B |
U A |
n |
|
. |
|
|
|
|
Z C |
U B |
|
. |
U C |
Векторная диаграмма ЭДС и линейных напряжений при соединении фаз генератора звездой:
|
|
А |
|
+j |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
. |
. |
|
|
|
. |
|
|
|
|
|
|
|
|
||||
|
UCA |
EA |
|
|
|
|
|
|
|
|
|
|
UAB |
|
|
||
|
|
|
|
|
|
|
||
|
|
N |
|
|
|
|
|
|
. |
|
|
|
|
. |
+1 |
||
|
|
|
|
|
|
|||
|
EC |
. |
EB |
В |
||||
С |
|
|||||||
UBC |
|
|||||||
|
|
|
|
|
||||
Линейные напряжения больше фазных ЭДС в 
 3 раз: Uл
3 раз: Uл 
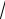 3Eфe j300 . При симметричной нагрузке когда Z A Z B Z C Z , напряжение смещение нейтралиUN 0 и фазные напряжения на нагрузке равны фазным
3Eфe j300 . При симметричной нагрузке когда Z A Z B Z C Z , напряжение смещение нейтралиUN 0 и фазные напряжения на нагрузке равны фазным
ЭДС: UA |
EA , UB |
EB , |
UC |
EC . |
Линейные (фазные) токи I A |
|
, |
|||||||
EA |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I |
|
EB |
, |
I |
|
EC |
равны по величине и сдвинуты друг относительно дру- |
|||||||
|
|
|||||||||||||
B |
|
Z |
C |
Z |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
га на1200 . |
|
|
|
|
|
|
|
|
|
|||||
|
|
Соединение «звезда – звезда» при несимметричной нагрузке |
|
|
||||||||||
Известны |
|
|
2 |
|
|
и Z A , Z B , Z C . |
|
|
||||||
EA |
, EB a EA ; |
EC |
aEA |
|
|
|||||||||
Найти все линейные токи: IA, IB , IC и ток в нейтральном проводе. 1.Нейтральный провод разомкнут Z N , следовательно U N 0 .
44
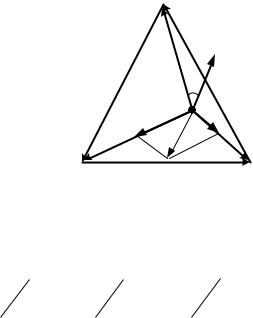
Так как в схеме имеются только два узла, проведем расчет методом узловых потенциалов. Пусть N 0 , тогда напряжение смещения нейтрали равно:
|
|
|
|
Y A |
EA Y B EB |
Y C |
EC |
|
||||||
|
|
|
U N |
n |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
Y A Y B |
Y C Y N |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
где Y A |
1 |
; Y B |
1 |
; Y C |
1 |
|
; Y N |
1 |
|
– проводимости соответст- |
||||
Z A |
Z B |
|
|
|
|
|
||||||||
|
|
|
|
Z C |
|
Z N |
|
|
|
|||||
вующих ветвей.
Возникает перекос фаз, когда фазные напряжения не равны фазным
ЭДС. |
По второму закону |
Кирхгофа |
находим фазные |
напряжения |
|||||||||||||||
UA EA |
UN |
,UB |
EB |
UN |
,UC |
EC |
UN |
и линейные токи I A |
|
|
|
; |
|||||||
EA |
U N |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
I EB |
U N |
; I |
EC |
U N . |
|
|
|
|
|
|
|
Z A |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
Z B |
|
|
Z C |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Векторная диаграмма построена при активной нагрузке в фазах В и С Z B Z C R и при включении в фазу А катушки индуктивности
Z А RK jX L
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
. |
|
|
arctg |
X L |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UAB |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RK |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
. |
|
|
|
. |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
U |
|
|
UA |
|
|
|
IA |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
CA |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
. |
|
|
|
n |
IB |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
IC |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
UC |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
UB |
В |
|
|
|
|||
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
UBC |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
UN |
2.Нейтральный |
|
провод |
|
|
замкнут Z N 0 |
, следовательно |
|||||||||||||||||
IN Z N 0 , N n , перекос фаз |
устраняется, |
поэтому UA |
EA ; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UB |
EB |
; UC |
EC . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EA |
|
EB |
|
|
|
|
|
EC |
|
|
|
|
|
|
|
|
|
||||
Тогда I |
|
|
|
; I |
|
|
|
; I |
|
|
|
; |
|
|
|
|
|
|
||||||
|
|
|
|
Z B |
|
|
Z C |
|
|
|
|
|
|
|||||||||||
|
|
A |
|
|
Z A |
B |
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ток нейтрального провода I |
|
I |
I |
|
I |
|
U N |
. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
N |
|
|
A |
|
B |
|
C |
|
Z N |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
45
|
|
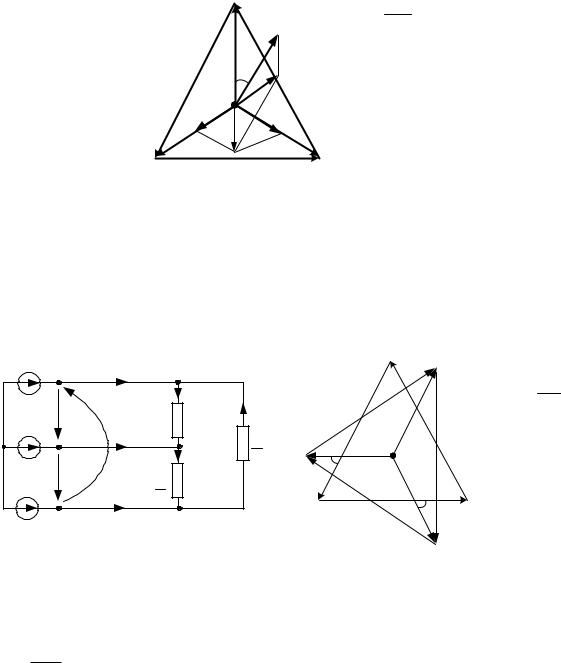
Векторная диаграмма построена при активной нагрузке в фазах В |
|||||||||||||||||||||||
и С Z B Z C R и при включении в фазу А катушки индуктивности |
|||||||||||||||||||||||||
Z А RK jX L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
А . |
|
|
|
arctg |
X L |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
UAB . |
|
RK |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
. |
|
|
. |
|
|
IA |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
UA |
|
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
UCA |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
n |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IC |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
IB |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
UC |
. |
|
|
UB |
В |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
UBC |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Соединение «звезда – треугольник» |
|
|
|
|
||||||||||||||||
|
|
Линейные |
напряжения |
|
|
|
|
|
|
являются одновременно |
|||||||||||||||
|
|
UAB ,UBC ,UCA |
|
||||||||||||||||||||||
фазными напряжениями на нагрузке. Токи IAB , IBC , ICA являются фаз- |
|||||||||||||||||||||||||
ными токами, а токи IA , IB , IC – линейными токами. |
|
|
|
|
|||||||||||||||||||||
|
|
. |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||
|
|
А |
|
I A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X L |
||||
|
|
|
|
. |
|
|
|
|
|
. |
|
|
. |
|
|
|
UCA |
|
|
arctg |
|||||
|
|
|
. |
|
|
|
|
|
I AB |
ICA |
|
|
|
|
|
RK |
|||||||||
|
|
. |
UCA |
Z |
|
. |
|
|
|
. |
. |
|
|
||||||||||||
|
|
EB |
UAB |
|
. |
|
|
|
|
|
|
|
|
IA |
|
. |
IAB |
IB |
|
|
|
||||
|
|
В |
|
IB |
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|||
N |
|
|
|
|
|
|
. |
|
|
|
|
|
|
ICA |
|
. |
|
|
|
||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
I BC |
|
|
|
|
|
|
|
UAB |
|
|
||||||
|
|
. |
UBC |
|
. |
|
|
|
|
|
|
|
|
|
|
|
IBC |
|
|
||||||
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
EC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
С . |
|
|
. |
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
UBC |
IC |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
и |
Z AB Z BC ZCA Z Ze |
j |
. |
|
|||||||||
Известны EA , |
EB |
a |
EA |
; EC aEA |
|
|
|||||||||||||||||||
Найти линейные и фазные токи. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Определим линейное напряжение |
|
|
|
|
|
|
, |
тогда по закону Ома |
|||||||||||||||||
UAB |
EA EB |
||||||||||||||||||||||||
I |
|
|
|
|
a2 I |
|
|
I |
|
aI . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
U AB и I |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
AB |
Z |
BC |
|
|
AB |
CA |
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По первому закону Кирхгофа определим линейные токи: |
|
|
|
||||||||||||||||||||||
I |
I |
I ; I |
I |
|
I |
; I I |
|
I . |
|
|
|
|
|
|
|
|
|||||||||
А |
|
АB |
CA |
B |
|
BC |
|
АB |
|
С |
СА |
|
BC |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
|
|

При симметричной нагрузке I |
|
|
I |
e j300 |
, следовательно |
3 |
|||||
л |
|
|
ф |
|
|
I А 
 3I АВe j300 , IB a2IA , IC aIA . Векторная диаграмма построена для симметричной нагрузки при включении в фазах катушки индуктивности
3I АВe j300 , IB a2IA , IC aIA . Векторная диаграмма построена для симметричной нагрузки при включении в фазах катушки индуктивности
Z АB Z BC Z CA RK jX L .
ТЕМА 8. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
Для расчета несимметричных режимов в линейных трехфазных цепях может быть использован метод симметричных составляющих, так как он сводит сложную задачу при наличии несимметрии ЭДС, токов и напряжений к нескольким более простым задачам расчета той же цепи при симметричных режимах[5].
Метод симметричных составляющих относится к специальным методам расчета трехфазных цепей и широко применяется для анализа несимметричного (аварийного) режима динамических трехфазных цепей (генераторы, двигатели, трансформаторы, линии), в том числе с нестатической нагрузкой. В основе метода лежит представление несимметричной трехфазной системы переменных (ЭДС, токов, напряжений и т.п.) в виде суммы трех симметричных систем, которые называют сим-
метричными составляющими.
Различают симметричные составляющие прямой ( A1, B1, C1 ), обратной ( A2 , B2 , C 2 )и нулевой ( A0 , B0 , C0 )последовательности.
Симметричные составляющие отличаются друг от друга порядком чередования фаз. Угол сдвига фаз между следующими друг за другом фазными величинами данной последовательности определяется форму-
лой |
|
2 / 3 , |
где = 0, 1, 2 – индекс последовательности. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
A1 |
|
|
A1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
A2 |
C2 |
|
|
|
|
A0 B0 |
C0 |
|||||
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
||
|
|
120 |
|
|
|
B2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
C1 |
B |
|
|
|
||||
|
|
A0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
C1 |
|
|
|
|
B0 |
B1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
B |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
C0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47

Таким образом, симметричные составляющие можно записать в таком виде:
прямая последовательность |
( = 1): A |
aB a2 C ; |
|
|||
|
1 |
1 |
|
1 |
|
|
обратная последовательность ( = 2): A |
a2 B |
2 |
aC |
2 |
; |
|
|
2 |
|
|
|
||
нулевая последовательность |
( = 0): A0 |
B0 C0 . |
|
|
||
Несимметричная трехфазная система векторов, обозначенных A, B, C представляет собой сумму векторов ее симметричных составляющих:
A A1 A2 A0 ;
B B1 B2 B0 a2 A1 a A2 A0 ;C C1 C2 C0 a A1 a2 A2 A0.
Сложим эти три уравнения с учетом, что a2 a 1 0 , получим:
A0 ( A B C) 3.
3.
A1 (A aB a2C) 3;
3;
A2 (A a2B aC) 3.
3.
Очевидно, что симметричная система ЭДС данной последовательности вызывает в симметричном приемнике симметричные системы токов и напряжений той же самой последовательности. В этом заключа-
ется принцип независимостидействия симметричных составляющих в симметричной трехфазной цепи. Поэтому метод симметричных составляющих, как своеобразный метод наложения, идеально подходит для расчета токов и напряжений в цепи, где несимметричная система ЭДС подключена к симметричной нагрузке.
Система нулевой последовательности представляет собой неуравновешенную систему и считается симметричной только по формальным признакам. Отдельные подсхемы, в которых действует каждая из симметричных составляющих этой системы, могут отличаться как конфигурацией, так и величиной сопротивлений в силу особенностей поведения этих составляющих даже в симметричной трехфазной цепи.
При расчете несимметричных режимов трехфазных цепей методом симметричных составляющих необходимо учитывать следующие особенности:
1. В трехфазной цепи с нейтральным проводом ток в нем равен сумме линейных токов, т. е. утроенному значению составляющей нулевой последовательности этих токов:
IN IA IB IC 3IЛО
48
В цепи же без нейтрального провода сумма линейных токов равна нулю, поэтому линейные токи не могут иметь составляющих нулевой
последовательности: IЛО 0 .
2.Сумма линейных напряжений всегда равна нулю, поэтому они не содержат составляющих нулевой последовательности: UЛО 0 .
3.Фазные напряжения симметричной статической нагрузки, соединенной звездой, не содержат составляющих нулевой последовательности, отсюда сумма фазных напряжений равна нулю. Действительно,
поскольку Y A Y B Y C , то
UA |
(UABY B UCAY A ) / (Y A Y B Y C ) (UAB |
UCA ) / 3. |
|||||
|
|
|
(UBC |
UAB ) / 3, |
|
|
|
Аналогично, UB |
UC |
(UCA |
UBC ) / 3. |
||||
|
|
|
|
|
|
|
|
Тогда UФО |
(UА UB UC ) / 3 0 . |
|
|
||||
|
|
|
|
|
|
|
|
4. Сопротивления фаз нагрузки токам разных последовательностей в общем случае различны:
Z1 |
U A1 |
/ I A1 |
UB1 |
/ IB1 |
UC1 |
/ IC1 |
U1 |
/ I1; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
U |
2 |
/ I2 ; |
Z 0 |
U0 |
/ I0. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Нормальным режимом работы динамической трехфазной цепи является симметричный режим. В некоторых случаях (как правило, связанных с авариями – обрыв линейного провода, короткое замыкание фазы и т. п.) в цепи появляется несимметричный участок. Остальные участки симметричны, в том числе источники электрической энергии. Такая цепь называется цепью сместной несимметрией.
Если на основе теоремы компенсации заменить несимметричный участок соответствующей трехфазной системой источников напряжения или тока, то получится симметричная цепь, в которой действует несимметричная трехфазная система ЭДС или токов эквивалентных источников. В соответствии с условиями замены можно составить необходимые дополнительные уравнения для их определения. Такую цепь можно рассчитывать методом симметричных составляющих.
Цепь с продольной несимметрией имеет несимметричный уча-
сток, включенный последовательно в фазы линии или нагрузки.
A I А
Симметр. B источник I В
|
|
C I |
IN |
|
C |
Несимметр. участок
ZNn |
a |
|
|
|
U A |
|
|
|
|
|
|
|
|
|
b |
Симметр. |
A |
I A |
|
UB |
a |
|
|
|
|
|
|
b |
c |
приемник |
B |
IB |
|
|
|
|
|
C |
|
|
c |
|
|
|
IC |
|
|
||
|
|
|
|
UC |
||
|
|
|
|
|
49
Согласно теореме компенсации заменим фазы этого участка источниками ЭДС, которые равны падениям напряжения на элементах участка. В результате получим симметричную цепь с несимметричным трехфазным источником. Если комплексные сопротивления фаз несимметричного участка известны, то вводимые вместо них фазные ЭДС
связаны с токами законом Ома: UA IA Z A;UB IB Z B ;UC IC Z C ;
Это условия несимметрии, которые следует использовать вместе с уравнениями метода симметричных составляющих для определения не-
известных токов IA, IB , IC и напряжений UA , UB , UC . Сопротивления
могут принимать любые значения от нуля и до бесконечно больших величин. Например, в случае обрыва линейного провода между точкамиА и а и неповрежденных проводах двух других фаз окажется Z A .
Если сопротивлениями проводов линии пренебречь или включить их в параметры симметричных участков, то условия несимметрии будут вы-
глядеть так: IA 0, |
UB 0, |
UC 0. |
|
|
|
Цепь с поперечной несимметрией имеет несимметричный уча-
сток, подключенный параллельно фазам нагрузки или между фазами линии и нулевым проводом, роль которого может играть и «земля».
С помощью теоремы компенсации получаем, как в предыдущем случае, симметричную цепь с несимметричной системой эквивалентных ЭДС. Условия несимметрии при известных сопротивлениях фаз несимметричного участка останутся теми же Z A , ZB , ZC .
Симметричный |
источник |
IN 
A
B
C
I А  I В
I В IС
IС 
Несимметр. участок
ZN |
0 |
Zn |
|
Симметричный приемник |
|
|
|
|
I n |
|
|
A B C
U A IС
U B
UС
I А I B
0
Иногда удобно использовать замену несимметричного участка системой эквивалентных источников тока IA, IB , IC . Например, при ко-
ротком замыкании одной фазы линии (А) на землюв системе генератор– двигатель, фазы которых соединены звездой, причем нейтральная точка генератора заземлена:
50
