
ТОЭ / ТОЭ ТПУ
.pdf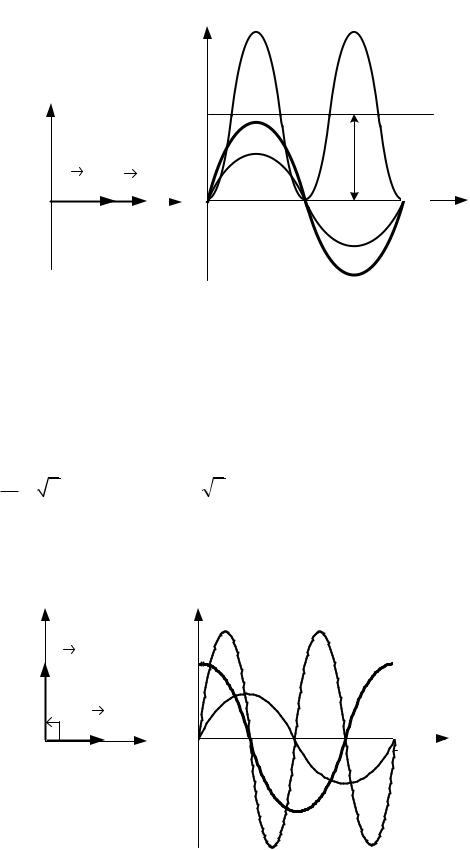
p ui 2I 2Rsin2 ( t i ) I 2R(1 cos2( t i )) .
p(t)
ψi=0
Р
Im Um
|
|
0 |
π |
|
2π ωt |
|
|
|
|
|
|
i(t) |
|
|
|
|
u(t) |
|
||
|
|
|
|
1 |
T |
|
Средняя за периодТ активная мощность: Р |
p(t)dt I 2 R, Вт . |
|||||
T |
||||||
|
|
|
|
0 |
||
|
|
|
|
|
||
P – называется активной мощностью и используется в балансе активных мощностей.
Индуктивность в цепи синусоидального тока
При токе i(t) Im sin( t i ) , по закону электромагнитной индукции:
u L dtdi 
 2I Lcos( t i )
2I Lcos( t i ) 
 2U sin( t i 900 )
2U sin( t i 900 )
Для действующих значений: U I L IX L , где X L L,Ом – индук-
тивное реактивное сопротивление.
Напряжение на индуктивности опережает ток на 900 , т.е. угол сдвига фаз 900 .
|
|
|
p(t) |
U m |
|
|
|
900 |
ψi=0 |
i(t) |
|
I m |
|
|
|
|
0 |
π |
2π ωt |
|
|
|
u(t) |
21

Мгновенная активная мощность:
p ui 2I 2 XL sin( t i )cos( t i ) QL sin 2( t i )) ,
где QL I 2 X L , вар (вольт-ампер реактивный) – индуктивная реактивная мощность, применяется в балансе реактивных мощностей.
1 T
Средняя за периодТ активная мощность: Р T 0 p(t)dt 0 .
Когда p 0 индуктивность запасает энергию в магнитном поле, тогда
p 0 , запасенная энергия возвращается в сеть. |
|
|
|
|
|
||||||||||||||
|
|
|
|
Ёмкость в цепи синусоидального тока |
|
||||||||||||||
При |
токе |
i(t) Im sin( t i ) |
|
|
для |
напряжения |
получим: |
||||||||||||
|
1 |
|
|
|
|
|
I |
cos( t i ) |
|
|
|
|
|
|
|
||||
u |
|
i(t)dt |
|
2 |
|
2U sin( t i |
900 ) . |
|
|||||||||||
С |
|
|
|||||||||||||||||
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
||||
Для действующих значений: U |
I |
IX |
|
, где X |
|
|
1 |
, Ом – емкост- |
|||||||||||
|
C |
C |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
С |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ное реактивное сопротивление. Напряжение на ѐмкости отстает от тока
на 900 , т.е. угол сдвига фаз |
900 . |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(t) |
u(t) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
ψi=0 |
|
|
|
i(t) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
I m |
|
|
0 |
|
|
π |
|
|
2π ωt |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
900 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Um |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мгновенная активная мощность: |
|
|
|
|
|
|
|
|
|||||||||||||||
р u i 2I 2 X |
C |
sin( t |
) cos( t |
) Q |
sin 2( t |
) , |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
C |
|
|
i |
|
|
|
||
где Q I 2 X |
C |
, вар – |
емкостная реактивная мощность, применяется в |
||||||||||||||||||||
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
балансе реактивных мощностей. |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
|
|
||
Средняя за периодТ активная мощность: |
Р |
p(t)dt 0 . |
|||||||||||||||||||||
T |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
22
Когда p 0 ѐмкость запасает энергию в электрическом поле, p 0 , за-
пасенная энергия возвращается в сеть.
Последовательное соединение R, L,C
i |
R |
|
UC |
|
|
|
c |
|
|
||
|
|
|
|
|
|
u |
|
L |
U |
UL |
I |
|
|
||||
|
|
|
|
|
|
|
C |
|
UR |
b |
|
|
|
|
|
|
|
|
|
|
ψi |
|
|
|
|
|
a |
|
|
|
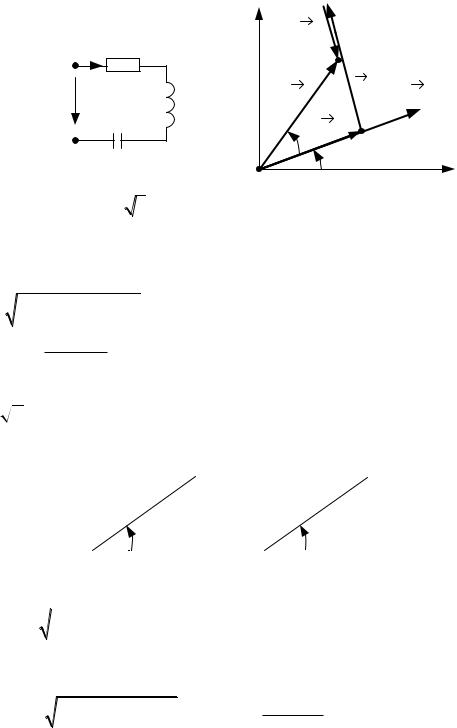
При токе i |
|
2I sin( t i ) , по 2 закону Кирхгофа входное на- |
|||||
пряжение равно: u uR uL uC . |
||||||||
|
Построим векторную диаграмму для действующих значений тока |
|||||||
и |
напряжений.Получим треугольник напряжений abc, где |
|||||||
|
|
|
|
|
|
|
|
|
U |
U 2 U |
L |
U |
C |
2 – действующее значение входного напряжения, |
|||
|
|
R |
|
|
|
|
||
arctg UL UC – сдвиг фазы между входным напряжением и током
UR
(угол нагрузки),
u 
 2U sin( t i ) – мгновенное значение входного напряжения.
2U sin( t i ) – мгновенное значение входного напряжения.
На основании треугольника напряжений получаем треугольник сопротивлений и треугольник мощностей:
|
|
|
|
Z |
|
|
S |
|
|
|
|
|
|
|
|
XL- X C |
|
|
|
QL- QC |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
P |
|
|
|
Из треугольника сопротивлений: |
|
|
|
|
||||||
|
U |
|
|
|
X L X C |
|
|
|||
Z |
|
R2 X L X C 2 , arctg |
, |
|
||||||
I |
|
R |
|
|||||||
|
|
|
|
|
|
|
|
|
||
где Z (Ом) – полное сопротивление цепи. Из треугольника мощностей:
. S UI P2 QL QC 2 , arctg QL QC ., P
23
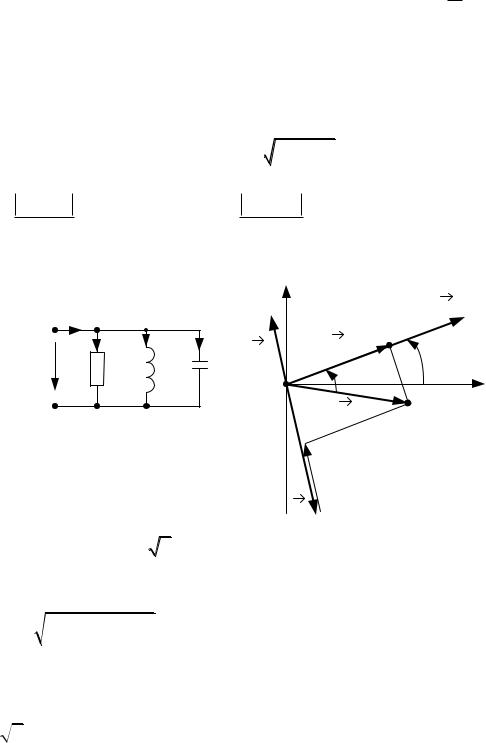
где S , ВА (вольт-ампер) – полная мощность цепи; cos P – коэффи- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
циент мощности. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
На основании треугольника мощностей составляется баланс мощ- |
||||||||||||
ности электрической цепи. |
|
|
|
|
|
|
|
|
||||||
а) мощность источников: Sи UI , |
Pи S cos , |
Qи S sin . |
||||||||||||
б) потребляемая мощность: |
|
|
|
|
|
|
|
|||||||
P I 2 R, |
Q I 2 X |
L |
I 2 X |
C |
, |
|
S |
п |
P2 |
Q2 . |
|
|||
|
п |
|
п |
|
|
|
|
|
|
|
|
|||
Погрешность расчета (небаланс): |
|
|
|
|||||||||||
|
P |
Pи Рп 100% 3% , |
|
|
Q |
Qи Qп 100% 3% |
||||||||
|
Ри |
|
|
|
|
|
|
|
|
Qи |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Параллельное соединение R, L,C . |
||||||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iR |
|
|
iL |
|
iC |
|
|
|
IR |
b |
|
|
|
u |
|
|
|
|
|
I c |
ψU |
|||||
|
|
R |
L |
C |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I L |
|
При напряжении u |
2 U sin( t u ) , |
по 1 закону Кирхгофа входной |
||||||||||||
ток равен: |
i iR iL iC . Построим векторную диаграмму для дейст- |
|||||||||||||
вующих значений напряжения токов. Получим треугольник токов abc, |
||||||||||||||
где I 
 IR2 IL IC 2 – действующее значение входного тока,
IR2 IL IC 2 – действующее значение входного тока,
arctg |
IL IC |
– сдвиг фазы между входным напряжением и током |
|
||
|
IR |
|
(угол нагрузки).
i 
 2I sin( t u ) – мгновенное значение входного тока.
2I sin( t u ) – мгновенное значение входного тока.
На основании треугольника токов получаем треугольник проводимостей.
24
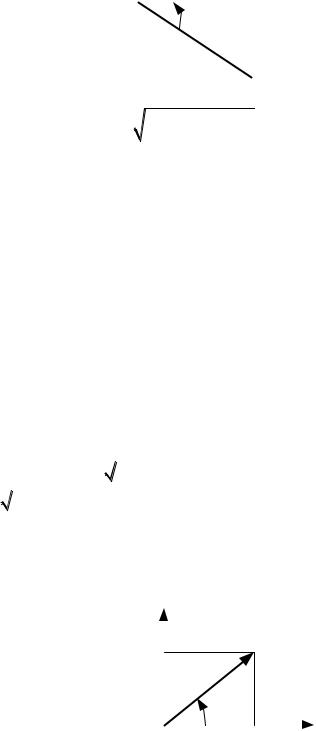
g
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bL - bC |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
Из треугольника проводимостей: |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
, arctg |
bL bC |
, |
|
|
|
|
|
|
|
|
Y |
|
|
g2 b |
b |
2 |
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
U |
|
L |
C |
|
|
|
g |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где Y , См (Сименс) – полная проводимость цепи; |
|||||||||||||||||
g |
|
1 |
, См – активная проводимость; |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
|
1 |
|
, См – индуктивная реактивная проводимость; |
|||||||||||||
|
|
|
|||||||||||||||
L |
|
|
|
X L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
|
1 |
|
, См – емкостная реактивная проводимость. |
|||||||||||||
|
|
|
|
||||||||||||||
C |
|
|
|
XC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Изображение синусоидальных токов и напряжений комплексными числами
Синусоидальной функции времени напряжения или тока соответствует изображение в виде комплексного числа (КЧ) на комплексной плоскости.
|
|
|
|
|
|
|
) I Ie j i |
|
|
|
|
i |
2I sin( t |
i |
a jb , |
||
|
|
|
|
|
|
|
|
|
|
|
|
– мнимая единица; I |
|
||||
где j |
1 |
– комплекс действующего значения |
||||||
тока; Ie j i – |
показательная форма |
|
записи КЧ; |
a jb – алгебраическая |
||||
форма записи КЧ; a Re(Ie j i ) – действительная часть КЧ; b Im(Ie j i )
– мнимая часть КЧ.
+j |
|
|
I |
||
|
|||||
|
b |
|
|
||
|
|
|
|
|
|
|
|
|
ψi |
+1 |
|
|
|
|
|
|
|
|
|
|
|
a |
|
Система координат ( j, 1) называется комплексной плоскостью. (+1) – действительная ось, ( j )– мнимая ось.
Обе формы КЧ связаны тригонометрическими соотношениями:
25
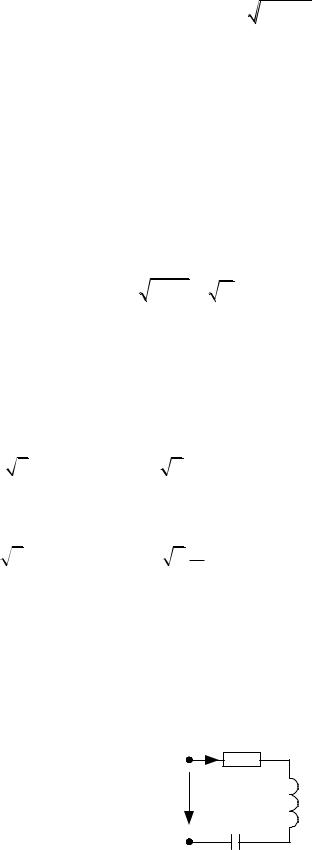
a I cos i , b I sin i , I |
|
|
arctg |
b |
|
|
a2 b2 , i |
1800 , |
|||||
a |
||||||
|
|
|
|
|
||
причем ( 1800 ) учитывается, когда a 0 .
Операции с комплексными числами.
1) сложение и вычитание:
A1 A2 (a1 jb1) (a2 jb2 ) (a1 a2 ) (b1 b2 ) a3 jb3 A3
2) умножение:
|
A1e |
j 1 |
A2e |
j 2 |
A1A2e |
j( 1 2 ) |
A3e |
j 3 |
|
|
|||||||||
A1A2 |
|
|
|
|
|
|
|
A3 |
|||||||||||
|
|
|
|
|
|
|
A1e |
j 1 |
|
A1 |
|
|
|
|
|
|
|
||
|
|
|
|
A1 |
|
|
|
|
|
j ( 1 2 ) |
|
|
j 3 |
||||||
3) |
деление: |
|
|
|
|
|
|
|
|
|
e |
|
|
A3e |
|
A3 |
|||
|
|
A2e |
j 2 |
A2 |
|
|
|
||||||||||||
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
||||
4) |
возведение в степень: (Ae j )n |
Ane j n |
|
||||||||||||||||
5)извлечение корня: n Ae j n
Ae j n Ae j n
Ae j n
6)комплексно-сопряжѐнное число A* : если A Ae j a jb , то
A* Ae j a jb
7)некоторые соотношения:
j e j900 ; |
( j) e j900 ; 1 e j 00 ; |
( 1) e j1800 ; |
1 |
j; |
j2 1 |
|
j |
||||||
|
|
|
|
|
8) дифференцирование:
т.к. (
 2Asin( t )) (
2Asin( t )) (
 2 Asin( t 900 ) , то
2 Asin( t 900 ) , то
(Ae j ) Ae j ( 900 ) j A
9) интегрирование:
т.к. 
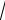 2 Asin( t i )dt
2 Asin( t i )dt 
 2 A sin( t i 900 ) , то
2 A sin( t i 900 ) , то
Ae j dt A e j ( 900 ) |
A |
j |
A |
||
|
|
|
|
|
|
|
j |
|
|
||
Законы электротехники в комплексной форме
а) Закон Ома.
|
I R |
U |
|
|
jX L |
|
|
|
-jXC |
26
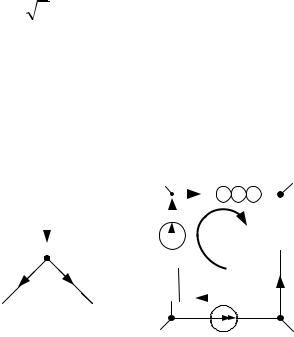
При токе i 
 2I sin( t i ) , в комплексной форме получим изображения действующих значений тока и напряжений на элементах:
2I sin( t i ) , в комплексной форме получим изображения действующих значений тока и напряжений на элементах:
I Ie j i , UR IR , UL IjXL , UC I ( jXC ) .
Полное комплексное сопротивление цепи: Z R jX L jXC
|
|
|
|
|
|
|
|
|
|
|
|
j( i ) |
||||||
По закону Ома входное напряжение равно: U I Z Ue |
|
|
||||||||||||||||
б) Первый закон Кирхгофа. Для узла а: I |
I |
I |
|
0 . |
||||||||||||||
|
|
|
|
|
|
I. |
1 |
2 |
3 |
|
||||||||
|
|
|
|
b |
|
jX L |
|
|
c |
|
|
|
||||||
|
. |
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
. |
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
1 |
|
|
|
|
|
|
-jXC |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
. |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
I2 |
|
I3. |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
R |
|
|
|
|
|
|
UJ |
|
|
|
|
I3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
. |
d |
|
J |
|
Ze j
Ue j u
г) Второй закон Кирхгофа. Для контура 1: UR UL UC UJ E
или I1R I2 jXL I3 ( jXC ) UJ E .
Баланс мощности в комплексной форме.
Для расчета мощности источников используется комплексносопряжѐнное значение тока.
мощность источников:
Sи E I * UJ J * Se j S cos jS sin Pи jQи
активная потребляемая мощность: Pп I 2 R
реактивная потребляемая мощность: Qп I 2 X L I 2 XC погрешность расчета (небаланс):
|
P |
|
|
|
Pи Рп |
|
|
100% 3% |
, |
|
Q |
|
|
|
Qи Qп |
|
|
100% 3% |
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Ри |
|
|
|
|
|
Qи |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
ТЕМА 3. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
Резонанс – это такой режим электрической цепи, содержащей емкости и индуктивности, при котором общее входное сопротивление или входная проводимость цепи будут резистивными. В этом режиме цепь потребляет только активную мощность и входные ток и напряжение совпадают по фазе.
27
Резонанс напряжений
Резонанс напряжений возникает при последовательном соединении участков цепи с индуктивным и емкостным характером. Входное сопротивление цепи: Z R j( X L X C ) .
Условие резонанса: X X |
|
|
или L 1 |
C |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I. |
|
|
|
R |
|
|
|
|
|
|
jX L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-jXC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Резонансные величины: |
|
1 |
|
|
|
|
|
|
; |
C 1 |
|
|
; L 1 |
|
2 |
|
|
. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
LC |
|
0 |
|
|
|
2 |
L |
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
L |
X |
C |
|
|
|
|
||||||||||
В режиме резонанса Z R ; |
|
|
|
|
|
|
U |
|
; arctg |
|
|
|
|
|
0 ; |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
R |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Q UI sin 0 ; |
S P UI cos I 2 R. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X L 1 C и arctg |
X |
|
|
|
||||||||||||||||||||||||||||||||||
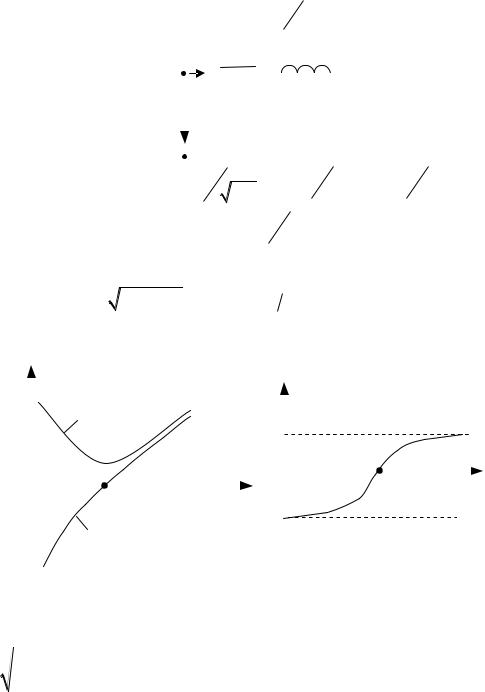
Зависимости Z R2 |
X 2 |
, |
от угловой |
|||||||||||||||||||||||||||||||||||||||||||||||
R |
||||||||||||||||||||||||||||||||||||||||||||||||||
частоты : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Z, X, R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Z( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
X( ) |
|
|
|
|
|
|
|
|
|
|
|
|
- 90 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если X L X C R , то UL jX L I |
, UC jXC I будут равны по модулю и |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
превысят входное напряжение U L UC U . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
L |
|
|
L |
1 |
[Ом] |
волновое |
(характеристическое) |
|
сопротивле- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
C |
0 |
|
0C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ние контура; G |
UL |
|
|
UC |
|
|
|
X L |
|
|
XC |
|
|
|
добротность контура, ко- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
U |
|
U |
|
|
|
R |
|
|
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
тораяопределяет резонансные свойства контура. Чем больше доброт-
28
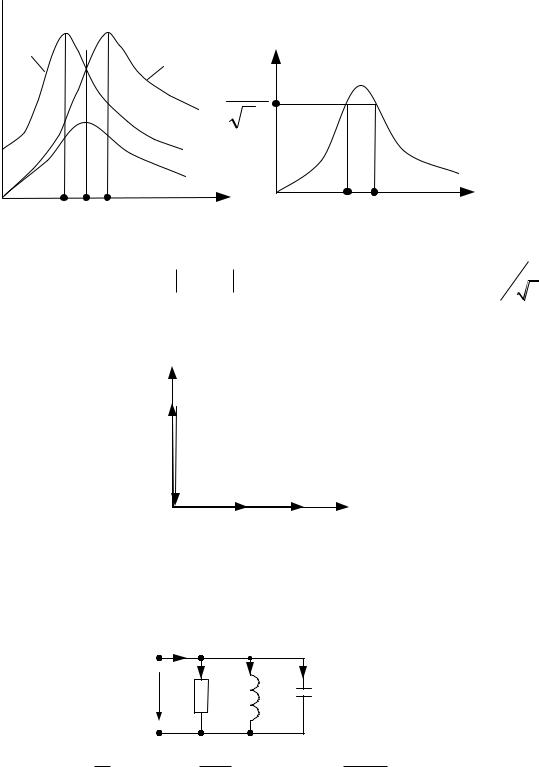
ность G , тем меньше отличаются L и C от резонансной частоты и тем острее становятся все три резонансные кривые I ( ) , UC ( ) , U L ( )
 I, UL ,UC
I, UL ,UC
UC |
UL |
|
I |
|
|
|
|
||
|
I max |
|
|
|
|
|
2 |
|
|
I |
|
|
|
|
|
|
|
|
|
C 0 L |
|
|
1 |
2 |
|
|
|
|
|
Полоса пропускания П |
0 |
определяется по уровню Imax |
||
|
1 2 |
G |
|
2 |
|
|
|
||
резонансной кривой тока I ( ) .
Векторная диаграмма резонанса напряжений
+ j |
|
|
|
. |
. |
|
|
UL |
|
|
|
UC |
|
|
|
|
. . |
I. |
|
|
UR U |
+1 |
Резонанс токов
Резонанс токов возникает при параллельном соединении участков
цепи с индуктивным и емкостным характером. |
|
|
||||||||||
|
|
|
|
I. |
I.R |
. |
I.C |
|
|
|||
|
|
|
|
. |
|
IL |
|
|
||||
|
|
|
|
|
R |
|
|
|
|
|
||
|
|
|
|
U |
|
jXL |
-jX C |
|
||||
|
|
U |
|
|
|
U |
|
|
|
U |
|
|
IR |
|
|
gU; IL |
|
|
UjbL ; IC |
|
|
UjbC , |
|||
R |
jX L |
jXC |
||||||||||
|
|
|
|
|
|
|
|
|
||||
29
где g 1 ; b |
1 |
; b |
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
L |
X L |
C |
|
X C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
По первому закону Кирхгофа: |
|
|
|
|
|
|
|
|
|
|
j(bC |
|
|
|||||||||
I |
IR IC |
IL |
U (g |
bL )) UY , |
||||||||||||||||||
где Y g j(bC bL ) – комплекс полной проводимости цепи. |
||||||||||||||||||||||
Условие резонанса токов: b |
b |
|
или |
1 |
L |
C. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
L |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Резонансные величины: 1 |
|
|
|
; C 1 |
2 |
|
; L 1 |
2 |
. |
|||||||||||||
|
|
|
|
|
|
0 |
|
|
|
LC |
0 |
|
|
L |
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|||||
В режиме резонанса токов проводимость Y g 1 |
R |
и входной ток бу- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дут минимальны; arctg bC bL |
|
0 ; Q UI sin 0 ; |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S P UI cos I 2 R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если g C 1 |
, то I |
L |
I |
C |
I ; |
y |
C волновая проводимость |
|||||||||||||||
|
0 |
0 L |
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
контура; |
G |
IL |
IC |
R |
|
R |
|
y |
добротность контура. |
|
||||||||||||
|
|
I |
I |
X L |
XC |
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
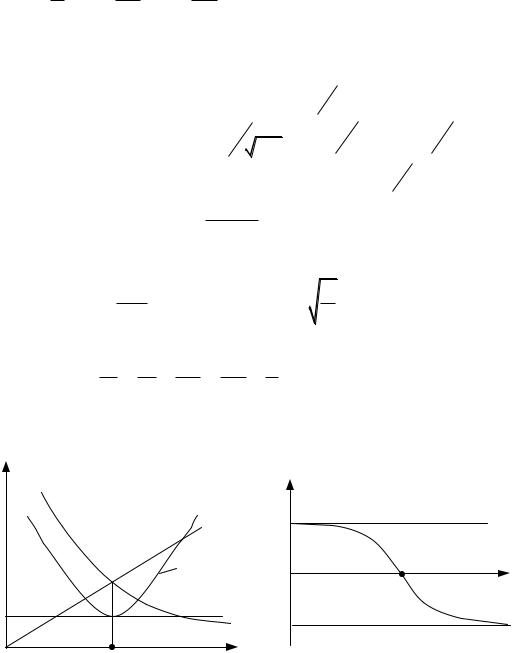
Частотные характеристики |
|
|
|
|
|||||||||||||||
I , I L , IC , I R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IL |
|
|
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IC |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I R |
|
|
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30
