ТОЭ / ТОЭ ТПУ

Добавил:

Werby Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

Теоретические основы электротехники

Файл:

нечное внутреннее сопротивление, и определяем: I

нечное внутреннее сопротивление, и определяем: I

.pdf

Скачиваний:

Добавлен:

21.06.2023

Размер:

2.23 Mб

Скачать

☆

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

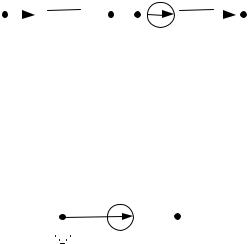
применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.Для расчета потенциалов в сложной электрической цепи необходимо составить лишь число NУ 1 независимых уравнений.

Токи в ветвях схемы выражаются с помощью закона Ома через потенциалы узлов:

a I1 R1 b c	E	R 2	I2 d
a I1 R1 b c		R 2	I2 d

I a b ( )g ;				I	2	c d E ( E)g				2
1		a	b 1		2		c	d		2
	R	1					R2
Потенциал		одного	из	узлов,			принятого	за	опорный

узел,принимается равным нулю. Если схема содержит ветвь с источником ЭДС без сопротивления, то за опорный узел берется любой из уз-

лов, к которым подключена эта ветвь. c

0, d

E .

Для остальных узлов составляются уравнения по 1 закону Кирхгофа для токов, выраженных через потенциалы узлов.

Правило составления уравнений для любого k-того узла произ-

вольной схемы в общем виде заключается в следующем:

gkk k gkm m Jkk .

Здесь gkk – узловая проводимость k-того узла, т.е. сумма проводимостей ветвей сходящихся в этом узле;

gkm – общая проводимость ветвей соединяющих узлы k иm;

J kk – узловой ток k-того узла.

Jkk Ekm gkm Jkm

1.Потенциал опорного узла принимается равным нулю;

2.Потенциал к-го узла k умножается на сумму проводимостей ветвей

подходящих к этому узлу;

3. Потенциал соседнегоm-узла m умножается на проводимость ветви,

соединяющейк-узел с m-узлом (всегда со знаком ―-‖);

4. В правой части записывается алгебраическая суммаподходящих к k-узлу токов источников тока и произведений ЭДС на проводимости своих ветвей, причем со знаком «+» берутся источники энергии направленные к рассматриваемому узлу k.

После определения потенциалов узлов схемы определяют токи в ветвях по закону Ома. Например, для схемы:

I1 R1	b I 3		c
	R	3	I	I4
		3	2
E1	UJ			R2	E2
	J
	a		a
Потенциал опорного	узла: a		0,	тогда	с E2 . Для узла

bсоставляем уравнение: b (g1 g3 ) c g3 a g1 E1g1 J . Определяем токи ветвей:

I1 ( a b E1 )g1, I2 ( c a )g2 , I3 ( b c )g3 .

По 1 закону Кирхгофа определяем ток: I4 I2 I3 . Напряжение на источнике тока равно: U J a b .

Метод наложения - это метод расчета, в котором используется принцип наложения. Принцип наложения заключается в следующем:

ток или напряжение в какой либо ветви можно рассматривать как алгебраическую сумму составляющих действующих от каждого источника в отдельности. Эти составляющие называются частичными.

Для расчета частичных токов и напряжений исходная схема разбивается на подсхемы, в каждой из которых действует один источник ЭДС или тока, причем остальные источники ЭДС считаются «закороткой» а источники тока разрывом ветви. Рассчитав частичные составляющие, определяются токи и напряжения исходной схемы. При этом со знаком «+» пишутся те составляющие, направление которых совпадает с направлением результирующих величин.

			Ik Ikчаст. ; Uk		Ukчаст. .
	Например, для схемы:
	R1	b	R1	b		R1	b
			I 2		I 2		I 2
E	J		R2 E		R2	J	R2
E			R2 E		R2	J	R2
	R3	a	R3	a		R3	a
	схема		1 подсхема			2 подсхема

В первой подсхеме размыкаем источник тока, имеющий беско-

Во второй подсхеме замыкаем источник ЭДС, имеющий нулевое внут-

реннее сопротивление, и определяем: I					J	R1 R3

				2		R1	R2	R3
						R1	R2	R3
Ток ветви равен: I2 I		I
Ток ветви равен: I2 I	2	I	2 .

Метод эквивалентного генератора (ЭГ). Любую сложную схе-

му, содержащую источники электрической энергии, относительно ветви

снагрузкой можно заменить активным двухполюсником. Этот двухполюсник можно преобразовать до двух эквивалентных параметров:

EГ

- ЭДС генератора и RГ - сопротивление генератора или

EГ

- источник тока генератора и R

- сопротивление генера-

RГ

тора.

Ток в нагрузке определяется по формуле Тевенена-Гельмгольца

для 1 схемы ЭГ:

EГ

по формуле Нортона-Поливанова

RГ RH

для 2 схемы ЭГ: IH

RГ

b IH

RГ

b I H

ЕГ

RH JГ

RГ

схема

1 схема ЭГ

2 схема ЭГ

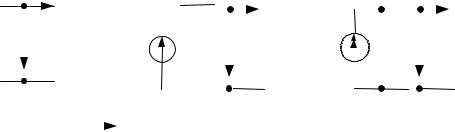
Параметры ЭГ можно определить тремя методами:

1)из опытов холостого хода (ХХ) и короткого замыкания (КЗ):

Вопыте ХХ: RH , I 0, U XX EГ ;

В опыте КЗ:	R	0, U		0, R		U XX	.
			H		Г
	H					IКЗ

	RГ	b		RГ b
					Iкз
ЕГ			Uxx ЕГ
ЕГ			Uxx ЕГ

a	a
опыт ХХ	опыт КЗ

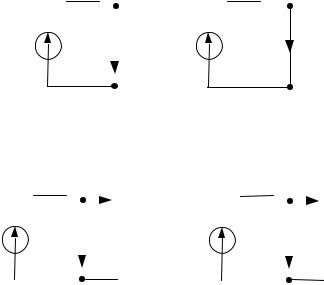
2) методом двух нагрузок:

RГ

b I 1

RГ

I 2

ЕГ

Задаются два разных сопротивления нагрузки R1 и R2 , измеряются

напряжения U1 , U2

и токи I1 , I2 . Составляется система уравнений по 2

U I R

закону Кирхгофа:

1 Г , после решения которой, получаем:

EГ U2 I2 RГ


E		U2 I1 U1I 2		, R	U2 U1		.
	Г
		I1	I2	Г	I1	I2

3) расчетнымметодом:

Для расчета выделяем ветвь, в которой определяем ток, считая оставшуюся часть цепи эквивалентным генератором. Размыкаем зажимы сопротивления выделенной ветви и определяем на них напряжение, которое является напряжением холостого хода генератора U XX , причем

U ЕГ , где ЕГ – ЭДС генератора. Сопротивление нагрузки RН равно

ХХ

сопротивлению выделенной ветви. Сопротивление генератора RГ равно

внутреннему сопротивлению генератора относительно разомкнутых зажимов. Оно определяется из схемы, в которой источники ЭДС считаются «закоротками» а источники тока– разрывом цепи. Определив эти параметры, рассчитываем искомый ток.

R	b I 3	R3	c	J	R	b	Uxx c
1	b I 3		c	J	1	b	Uxx c

E1	J		R 2	E2	E1	J	R 2	E2
	a	a				a	a
	расчетная схема					схема опыта ХХ

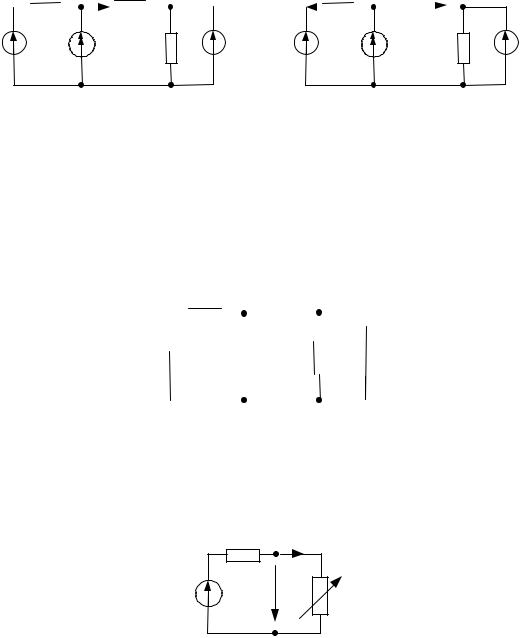
В расчетной схеме необходимо определить ток I3 . Рисуем схему опыта ХХ, в котором RH , и определяем по 2 закону Кирхгофа на-

пряжение холостого хода на разомкнутых зажимах нагрузки:

ЕГ U XX E1 E2 JR1 .

Для определения RГ рисуем вспомогательную схему, в которой источники ЭДС замкнуты, а источники тока разомкнуты:

	R1	b		R Г		c



							R 2



		a				a
Так как сопротивление R2		замкнуто накоротко, получаем: RГ R1 .
Определяем ток в нагрузке: I3			EГ		.
Определяем ток в нагрузке: I3		RГ		R3	.
		RГ		R3

Передача энергии от эквивалентного генератора в нагрузку.

RГ b I H

Е	U	R
Г	H	H
	H	H

Уравнение внешней вольтамперной характеристики (ВАХ) экви-

валентного генератора: U (I ) EГ IН RГ ;

Уравнение ВАХ нагрузки: U (I ) IН RН

Графическое решение этих двух уравнений позволяет определить ток в сопротивлении нагрузки RН :

U
Uхх		RН1
		RН1
UН1			RН2
			RН2
UН2
0	IН1	IН2	Iкз	I

Из уравнения баланса мощностей определяется мощность в нагрузке:

РН (IН ) EГ IН IН2 RГ

Из условия максимума функции: dPH EГ 2IН RГ 0 , получаем: dIH

I		EГ	. По формуле Тевенена–Гельмгольца: I			EГ
	Н	2RГ		Н	RГ	Rн

Условие максимальной мощности в нагрузке: RН RГ , такой режим ра-

боты называется согласованным.

КПД передачи энергии в нагрузку:

H Г

R R

(R R )

Г H

В согласованном режиме работы 0.5 Графические зависимости:

	P
Pmax
1		Pн(Iн)
0.5		(Iн)
		(Iн)
0	I кз 2	I кз	I

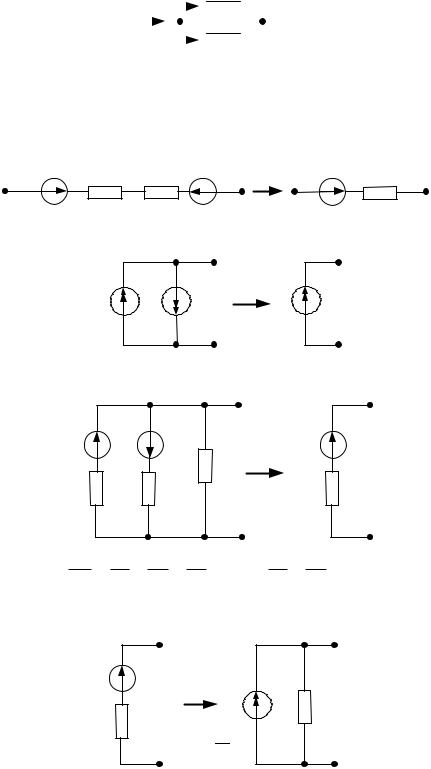
Эквивалентные преобразования электрических схем.

а) Правило распределения токов в параллельных ветвях («правило разброса»):

	I 3			I 1	R1






				I 2
				I 2	R2
					R2
I1 I3			R2		, I2 I3		R1
								.
		R R				R R		.
1			2		1		2

б) Последовательное соединение ЭДС и сопротивлений:

E1 R1

Eэ Rэ

ЕЭ E1 E2 , RЭ R1 R2 .

в) Параллельное соединение источников тока:

Jэ

JЭ J1 J2 .

г) Параллельное соединение ветвей с ЭДС и сопротивлениями:

E1	E2	Eэ
		R3
R1	R2	Rэ

1 1 1	1 , Е ( E1			E2 ) R .
RЭ R1 R2	R3	Э	R1	Э
RЭ R1 R2	R3		R1	R2
д) Эквивалентная замена источника ЭДС на источник тока и на-
оборот:
E
R			J	R
R	J	E
	J	E
		R

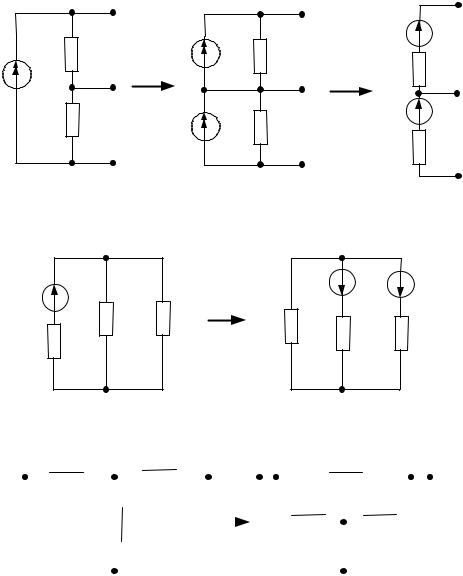
е) Перенос источника тока:

R1	J	R1	E1
			R1
J
R 2	J	R2	E2
			R2

где E1 J1R1, E2 J2 R2

ж) Перенос источника ЭДС через узел:

E1		E1		E1
E1
R 2	R3	R1	R 2	R3
R1		R1	R 2	R3
R1

з) Преобразование звезды в треугольник и наоборот:

R b

R ab

R c

Rca

Rbc

звезда

треугольник

Сопротивления сторон треугольника: R R R

Ra Rb

R R R

Rb Rc

R R R

Rc Ra

bc b

Сопротивления лучей звезды:

Rab Rca

, Rb

Rbc Rab

, Rc

Rca Rbc

Rab

Rab Rbc

Rca

Rab

Rbc Rca

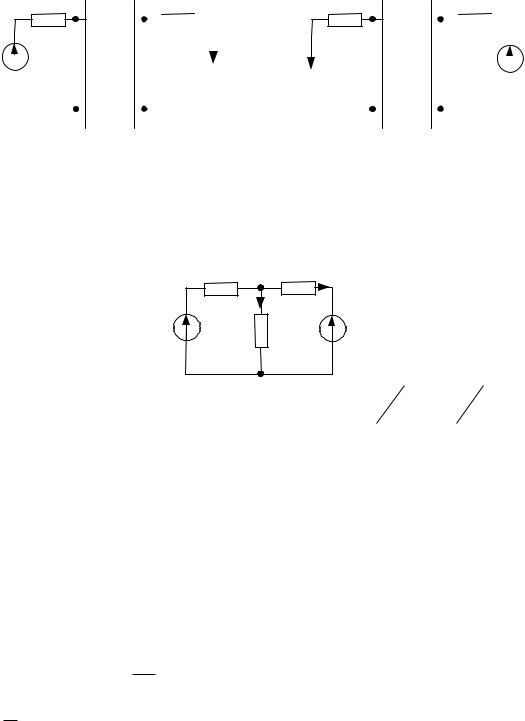
Свойства линейных цепей

а) Принцип взаимности. Применяется для цепи с одним источником ЭДС. Ток Icd в ветви cd, создаваемый ЭДС E , расположенной в

ветви ab, равен току Iab в ветви ab, если в ветвь cdпереместить ту же ЭДС E .

R1 b		d R1	R1 b		d R1

I2 I1

a c

I2= I1

б) Принцип линейности. В линейной цепи при изменении какоголибо из параметров (источника ЭДС, источника тока или сопротивления), любые две величины (токи или напряжения) связаны линейным соотношением вида: y ax b

	R1	R2	I
			2
		I3
E	R3		E
1			2

Если E1 var , тогда I3

aI2

b , где a

, b

ТЕМА 2. РАСЧЕТ ЦЕПЕЙ С СИНУСОИДАЛЬНЫМИ НАПРЯЖЕНИЯМИ И ТОКАМИ

Все законы и методы расчета линейных электрических цепей синусоидального тока сохраняют те же свойства, что и при расчете цепей постоянного тока.

Синусоидальный ток (напряжение) – это величина, мгновенное значение которой меняется по синусоидальному закону. Например, для тока i(t) Im sin( t i ) , где Im – амплитудное (максимальное) значе-

ние тока; 2 f 2T , радс (радиан/секунду) – угловая частота; f T1 , Гц (Герц) – частота; T , с (секунда) – период синусоиды;

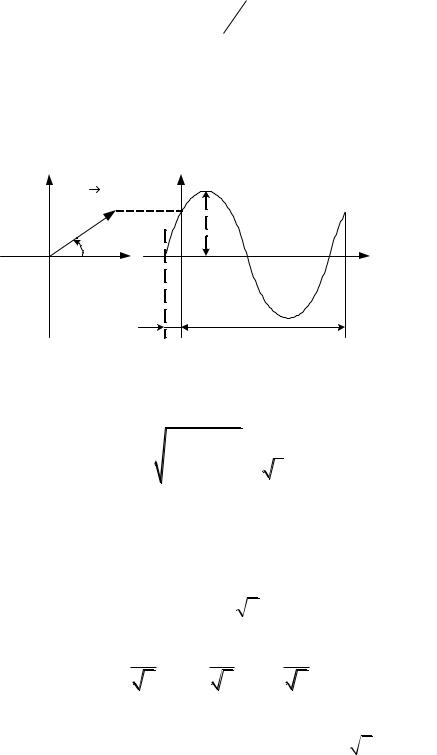
i , рад (радиан или градус, рад 1800 ) – начальная фаза.

В России: f 50 Гц., 314 рад с ,Т 0.02с.

Векторная диаграмма – это изображение синусоиды в виде вращающегося вектора в прямоугольной системе координат. Длина вектора равна амплитуде синусоиды. Угол поворота вектора равен начальной фазе и отсчитывается от оси абсцисс против часовой стрелки.

Волновая диаграмма – это график зависимости синусоидального тока от времени.

	i
Im	i(t)
	i(t)
ψi	Im
ψi
	ωt
ψi	T
векторная диаграмма	волновая диаграмма

Действующее илисреднеквадратичное значение синусоидально-

го тока определяется из соотношения

		1	T	I
I		1	i2 (t)dt	I	m	.
	T
				2
			0	2
			0

Физический смысл этого значения заключается в следующем: Действующее значение гармонического тока i численно равно такому постоянному току I , который за время T в том жесопротивлении R выделяеттакое же количества тепла W .

Исходя из вышеизложенного, действующие значения синусои-

дальных токов, напряжений и ЭДС в 2 раз меньше их амплитудных значений.

I Im2 , U U2m , E E2m .

Резистор в цепи синусоидального тока.

При токе i(t) Im sin( t i ) , по закону Ома u iR 2U sin( t i ) . Для действующих значений: U IR . Ток и напряжение в резисторе совпадают по фазе, т.е. угол сдвига фаз 0 .

Мгновенная активная мощность в резисторе:

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в папке ТОЭ

#
21.06.20232.23 Mб14ТОЭ ТПУ.pdf
#
21.06.20231.54 Mб11ТОЭ ТУСУР.pdf