
- •3. Методы спектрального анализа в нелинейных цепях
- •3.1. Основной принцип
- •Видно, что определение коэффициента нелинейных искажений сводится к определению амплитуд гармоник, то есть к гармоническому анализу тока .
- •3.2. Специальные методы спектрального анализа
- •3.3. Особенности спектрального анализа в цепях с нелинейными реактивными элементами
3. Методы спектрального анализа в нелинейных цепях
3.1. Основной принцип
Трансформация спектра входного сигнала в нелинейных цепях – важное явление. На нем основана работа целого ряда устройств: модуляторов, детекторов и т.д. С другой стороны, из-за нелинейности характеристики могут возникнуть и нежелательные эффекты, которые надо уметь оценивать и учитывать.
Рассмотрим
цепь, образованную последовательным
соединением источника гармонического
сигнала
![]() ,
источника постоянного смещения
,
источника постоянного смещения
![]() и
безинерционного нелинейного элемента.
На рис. 3.1 показано графическое построение
кривой, отображающей изменение тока в
безинерционной нелинейной цепи.
и
безинерционного нелинейного элемента.
На рис. 3.1 показано графическое построение
кривой, отображающей изменение тока в
безинерционной нелинейной цепи.

Рис. 3.1
Рис.
3.1 дает пример применения графического
метода проекций для
анализа прохождения сигнала в нелинейной
цепи. Видно, что форма тока и напряжения
здесь различны. Действительно,
![]() ,
а дифференциальная крутизна
,
а дифференциальная крутизна
![]() ВАХ нелинейного элемента на разных
участках различна. Поэтому одинаковым
приращениям
напряжения
на разных участках ВАХ отвечают различные
приращения тока.
ВАХ нелинейного элемента на разных
участках различна. Поэтому одинаковым
приращениям
напряжения
на разных участках ВАХ отвечают различные
приращения тока.
Теперь применим
аналитический спектральный метод
анализа прохождения сигнала в
нелинейной цепи. ВАХ нелинейного элемента
![]() считаем известной. Рабочая точка имеет
координаты
считаем известной. Рабочая точка имеет
координаты
![]() ,
где
,
где
![]() .
Пусть к зажимам нелинейного элемента
приложено, как и выше, напряжение
.
Пусть к зажимам нелинейного элемента
приложено, как и выше, напряжение
![]() .
ВАХ элемента запишем в параметрическом
виде:
.
ВАХ элемента запишем в параметрическом
виде:
![]() (3.1)
(3.1)
где
![]() .
Функция
.
Функция
![]() оказывается периодической четной
функцией аргумента
оказывается периодической четной
функцией аргумента
![]() с периодом
с периодом
![]() .
Разложим функцию
.
Разложим функцию
![]() в ряд Фурье:
в ряд Фурье:
![]() (3.2)
(3.2)
с
коэффициентами
![]() .
.
Так
как
![]() - четная функция
- четная функция
![]() ,
то ряд (3.2) содержит только косинусоидальные
члены и постоянную составляющую:
,
то ряд (3.2) содержит только косинусоидальные
члены и постоянную составляющую:
![]() (3.3)
(3.3)
где
![]() ,
,
![]() .
.
Анализ полученных результатов и выводы:
-
Спектр тока через нелинейный элемент обогащен гармониками частоты входного сигнала. Чем больше амплитуды гармоник
 ,
,
 ,
по сравнению с амплитудой первой
гармоники
,
по сравнению с амплитудой первой
гармоники
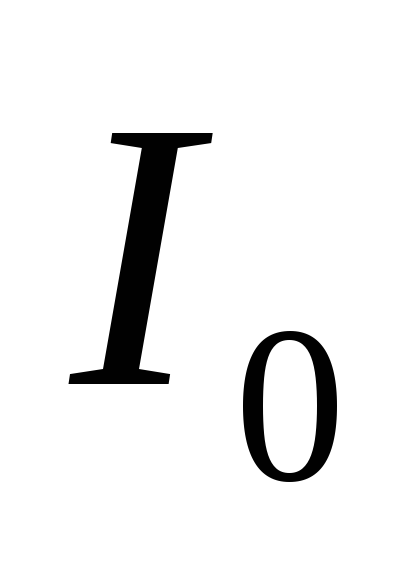 ,
тем сильнее искажения формы колебаний
тока гармониками.
,
тем сильнее искажения формы колебаний
тока гармониками.
-
Эти искажения принято характеризовать коэффициентом нелинейных искажений или коэффициентом гармоник
 (3.4)
(3.4)
Видно, что определение коэффициента нелинейных искажений сводится к определению амплитуд гармоник, то есть к гармоническому анализу тока .
-
Если переменная часть входного напряжения является четной функцией времени, то переменная часть тока через резистивный нелинейный элемент также является четной функцией времени.
-
Первая гармоника тока находится в фазе с переменной частью приложенного напряжения в виде гармонических колебаний.
-
Постоянная составляющая тока
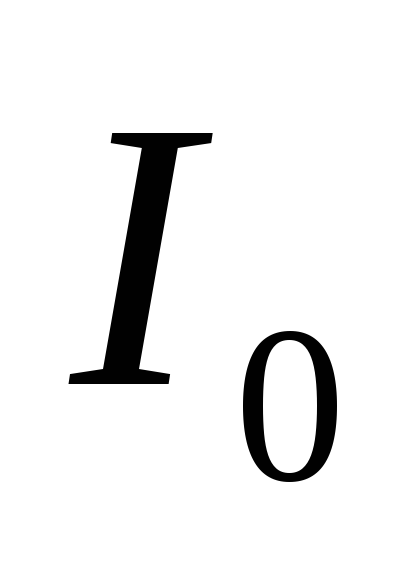 зависит и от смещения
зависит и от смещения
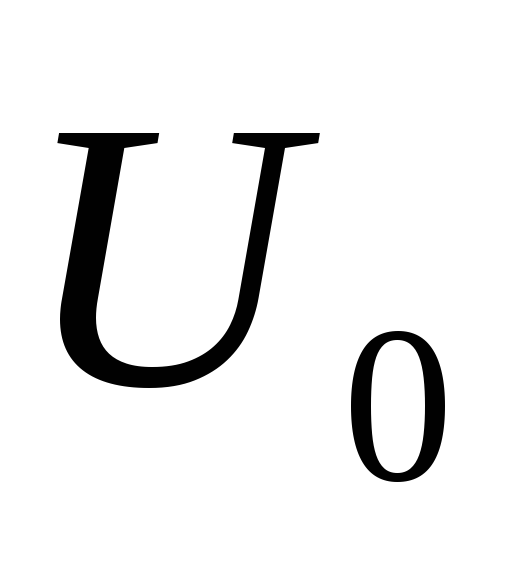 ,
и от амплитуды
,
и от амплитуды
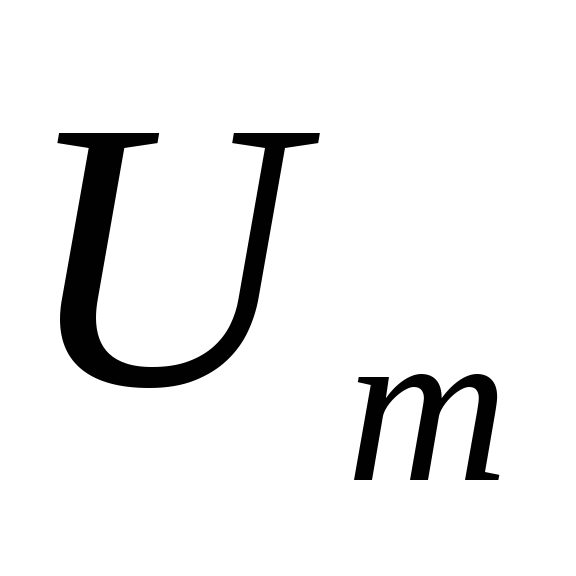 входного напряжения. То есть нелинейные
искажения испытывает не только
переменная, но и постоянная составляющая
тока через нелинейный элемент. В общем
случае постоянная составляющая тока
входного напряжения. То есть нелинейные
искажения испытывает не только
переменная, но и постоянная составляющая
тока через нелинейный элемент. В общем
случае постоянная составляющая тока
 отличается от значения тока в рабочей
точке
отличается от значения тока в рабочей
точке
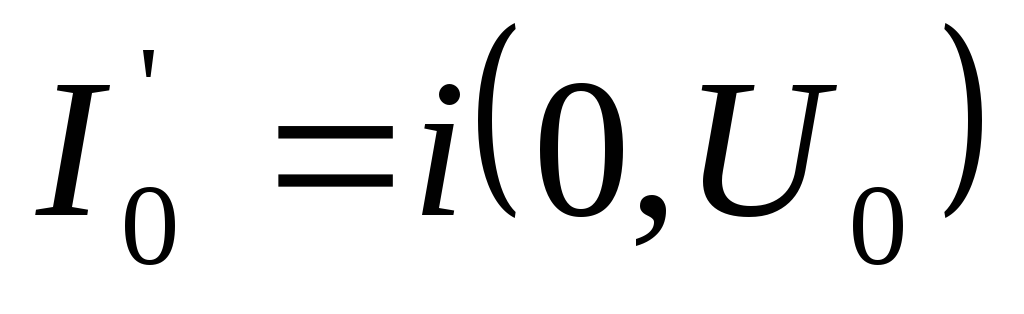 .
Так как крутизна
.
Так как крутизна
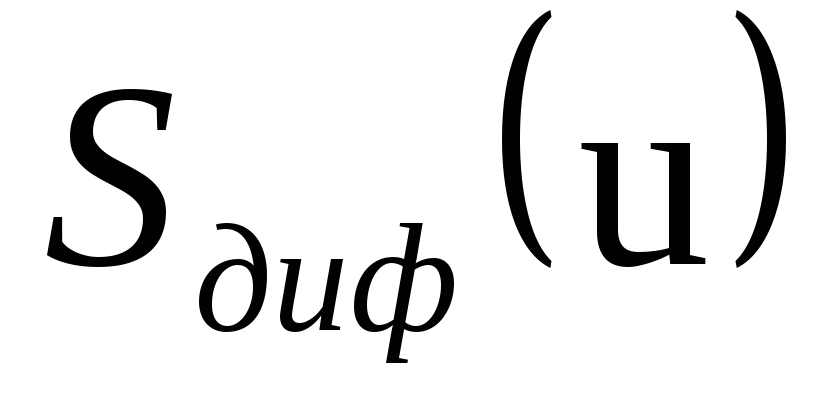 Так как
Так как
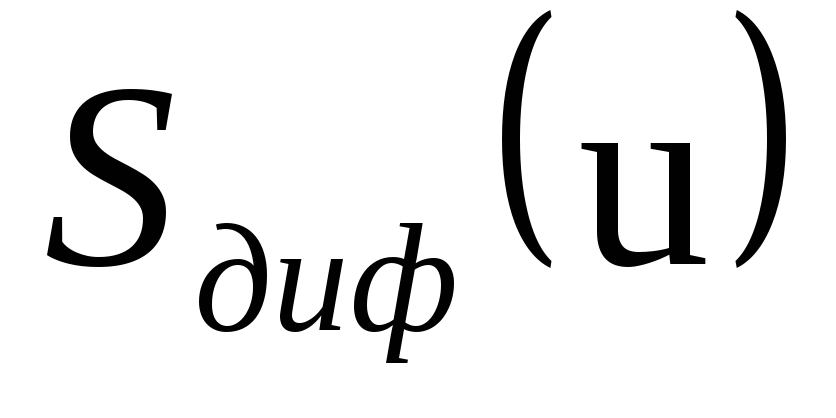 на рис. 3.1 возрастает с ростом напряжения
на рис. 3.1 возрастает с ростом напряжения
 ,
то
,
то
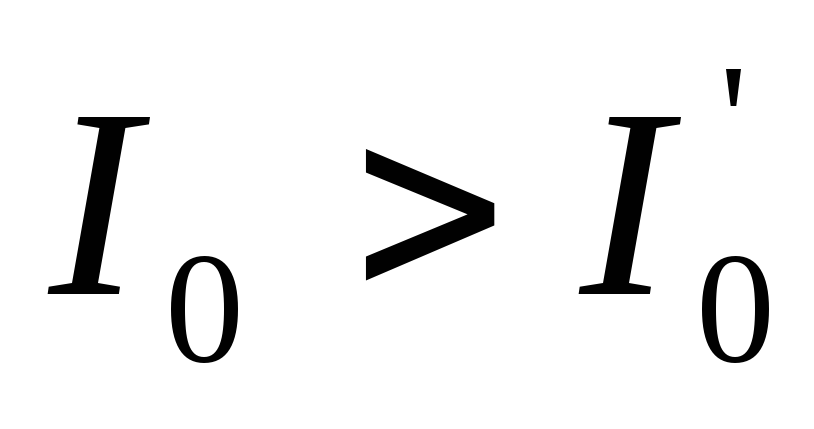 .
Зависимость постоянной составляющей
тока
.
Зависимость постоянной составляющей
тока
 от амплитуды переменного напряжения
– важная особенность нелинейных
элементов. На ней основана работа
выпрямителей, детекторов и многих
измерительных устройств.
от амплитуды переменного напряжения
– важная особенность нелинейных
элементов. На ней основана работа
выпрямителей, детекторов и многих
измерительных устройств.
