
nonlin / lect8
.doc5.13. Метод фазовой плоскости
Фазовая плоскость и фазовые траектории. Метод фазовой плоскости – качественный метод интегрирования дифференциальных уравнений второго порядка. Он широко применяется в радиотехнике, например, - для исследования автогенераторов, а также – в теории автоматического управления.
Дифференциальные уравнения второго порядка для автогенераторов, рассмотренных выше, можно записать в виде системы двух уравнений первого порядка:
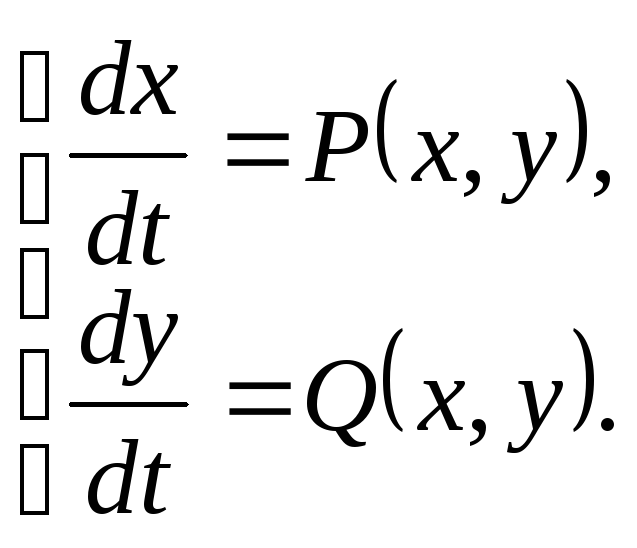 (5.90)
(5.90)
Для этого достаточно, например, для уравнения
![]() (5.46)
(5.46)
положить
![]() ,
,
![]() .
Тогда
.
Тогда
![]() и
и
![]() .
.
Фазовая плоскость
– это плоскость в координатах
![]() и
и
![]() .
Для интегрирования системы (5.90) надо
задать два начальных условия. В их
качестве часто задают начальные значения
.
Для интегрирования системы (5.90) надо
задать два начальных условия. В их
качестве часто задают начальные значения
![]() и
и
![]() в некоторый момент
в некоторый момент
![]() .
На фазовой плоскости состояние системы
в каждый момент времени
.
На фазовой плоскости состояние системы
в каждый момент времени
![]() определяется точкой с координатами
определяется точкой с координатами
![]() .
Последовательность состояний, проходимая
системой с течением времени из заданного
начального состояния, образует фазовую
траекторию. Скорость перемещения
вдоль фазовой траектории при изменении
состояния системы со временем – фазовая
скорость. Ее вектор направлен по
касательной к фазовой траектории в
каждой точке и имеет компоненты:
.
Последовательность состояний, проходимая
системой с течением времени из заданного
начального состояния, образует фазовую
траекторию. Скорость перемещения
вдоль фазовой траектории при изменении
состояния системы со временем – фазовая
скорость. Ее вектор направлен по
касательной к фазовой траектории в
каждой точке и имеет компоненты:
![]() и
и
![]() ,
величина фазовой скорости
,
величина фазовой скорости
![]() .
Направление скорости указывается
стрелкой.
.
Направление скорости указывается
стрелкой.
Фазовая плоскость, заполненная фазовыми траекториями, определяющими поведение системы при любых начальных условиях, называется фазовым портретом.
Уравнение фазовой траектории в дифференциальной форме получаем, исключая время путем деления второго из уравнений в (5.90) на первое:
![]() (5.91)
(5.91)
Для интегрирования (5.91) в большинстве случаев не удается использовать метод разделения переменных. Для построения фазовых траекторий часто используют графические и графо-аналитические методы: метод изоклин, метод Льенара, дельта-метод и т.д.
Изоклиной называется
линия, во всех точках которой угол
наклона
![]() касательной к фазовой траектории
одинаков. Уравнение изоклины
касательной к фазовой траектории
одинаков. Уравнение изоклины
![]() (5.92)
(5.92)
где
![]() .
.
Для заданного набора
значений
![]() ,
решая уравнение (5.92) для каждого из
значений
,
решая уравнение (5.92) для каждого из
значений
![]() по заданным функциям
по заданным функциям
![]() и
и
![]() находят и строят изоклины (см. рис. 5.28).
находят и строят изоклины (см. рис. 5.28).
![]()


![]()


![]()

![]()
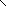


![]()
![]()





Рис. 5.28
Пунктирная кривая,
составленная из отрезков прямых линий
![]() ,
аппроксимирует фазовую траекторию,
проходящую через точки
,
аппроксимирует фазовую траекторию,
проходящую через точки
![]() ,
,
![]() ,
,
![]() … Угол наклона каждого из восстанавливаемых
отрезков
… Угол наклона каждого из восстанавливаемых
отрезков
![]() определяется в точке
определяется в точке
![]() как среднее арифметическое
как среднее арифметическое
![]() углов наклона фазовой траектории на
текущей и следующей изоклине. Чем чаще
построены изоклины, тем точнее будут
построены фазовые траектории. Построение
обычно начинают с изоклин вертикальных
и горизонтальных касательных. Согласно
(5.92), уравнение изоклины вертикальных
касательных
углов наклона фазовой траектории на
текущей и следующей изоклине. Чем чаще
построены изоклины, тем точнее будут
построены фазовые траектории. Построение
обычно начинают с изоклин вертикальных
и горизонтальных касательных. Согласно
(5.92), уравнение изоклины вертикальных
касательных
![]() (5.93)
(5.93)
для точек
![]() ,
где
,
где
![]() ,
а уравнение изоклины горизонтальных
касательных
,
а уравнение изоклины горизонтальных
касательных
![]() (5.94)
(5.94)
для точек
![]() ,
где
,
где
![]() .
.
Среди фазовых траекторий
особое значение имеют те, которые
определяют состояния равновесия и
режимы периодических колебаний. Особыми
точками
![]() на фазовой плоскости называются такие
точки, в которых
на фазовой плоскости называются такие
точки, в которых
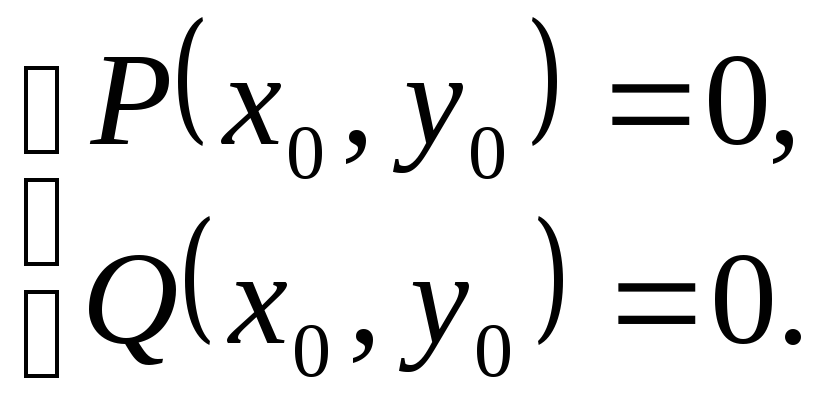 (5.95)
(5.95)
Из (5.95) следует, что в
особых точках фазовая скорость (с
компонентами
![]() и
и
![]() )
равна нулю.
)
равна нулю.
Вывод. Особые точки фазовой плоскости соответствуют состояниям равновесия системы.
Фазовые траектории бывают замкнутые и разомкнутые. Замкнутые траектории описывают режимы периодических колебаний и не содержат особые точки. По семейству фазовых траекторий можно определить:
-
Возможные состояния равновесия и их устойчивость;
-
Возможные периодические режимы (амплитуду, частоту и форму колебаний) и их устойчивость;
-
Характер переходных процессов при любых начальных условиях.
Типы особых точек. Пусть система описывается линейным дифференциальным уравнением
![]() (5.96)
(5.96)
Общее решение уравнения (5.96) с постоянными коэффициентами имеет вид:
![]() (5.97)
(5.97)
где
![]() и
и
![]() - постоянные величины, зависящие от
выбора начальных условий,
- постоянные величины, зависящие от
выбора начальных условий,
![]() и
и
![]() - корни характеристического уравнения
- корни характеристического уравнения
![]() ,
,
![]()
![]() (5.98)
(5.98)
Определение типов
реализующихся на фазовой плоскости
особых точек сводится к исследованию
характера фазовых траекторий около
этих точек. Характер фазовых траекторий
определяется свойствами коэффициентов
![]() и
и
![]() из (5.96). Особые точки для линейных систем
могут быть шести видов: центр, устойчивый
и неустойчивый фокус, устойчивый и
неустойчивый узел и седло.
из (5.96). Особые точки для линейных систем
могут быть шести видов: центр, устойчивый
и неустойчивый фокус, устойчивый и
неустойчивый узел и седло.
Пример. Колебания
в высокодобротном колебательном
![]() контуре:
контуре:
![]() ,
,
![]() ,
,
![]() .
Тогда (5.97) можно записать как
.
Тогда (5.97) можно записать как
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() определяются начальными условиями.
Далее,
определяются начальными условиями.
Далее,
![]() ,
или в полярных координатах:
,
или в полярных координатах:
![]() (5.99)
(5.99)
где
![]() ,
,
![]() ,
,
![]() .
.
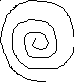
На фазовой плоскости системе (5.99) соответствует семейство фазовых траекторий в виде логарифмических спиралей, свертывающихся к началу системы координат. Они описывают квазигармонические колебания с затухающей по времени по экспоненциальному закону амплитудой. Одна из таких фазовых траекторий для некоторого выбора начальных условий показана на рис. 5.29, а.
![]()
![]()
![]()



![]()


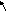

![]()
![]()

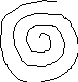
Рис. 5.29
Спираль на рис. 5.29, а
соответствует затухающему колебанию.
Начало координат соответствует устойчивой
(так как всякое отклонение от нее со
временем затухает) особой точке типа
устойчивого фокуса. Напротив, для
контура с отрицательным затуханием
(![]() ),
вносимым в контур, например, действием
положительной обратной связи, получим
фазовые траектории типа спиралей,
раскручивающихся относительно начала
координат (см. рис. 5.29, б). Им соответствуют
колебания, нарастающие по амплитуде со
временем. Соответственно, особая точка
(типа неустойчивого фокуса),
расположенная в начале координат, -
неустойчивая.
),
вносимым в контур, например, действием
положительной обратной связи, получим
фазовые траектории типа спиралей,
раскручивающихся относительно начала
координат (см. рис. 5.29, б). Им соответствуют
колебания, нарастающие по амплитуде со
временем. Соответственно, особая точка
(типа неустойчивого фокуса),
расположенная в начале координат, -
неустойчивая.
Если в (5.96)
![]() и
и
![]() ,
то получим систему, эквивалентную
идеальному контуру без затухания. В нем
могут реализоваться гармонические
колебания:
,
то получим систему, эквивалентную
идеальному контуру без затухания. В нем
могут реализоваться гармонические
колебания:
![]() .
Фазовые траектории имеют вид эллипсов
с центром в начале координат (см. рис.
5.30). В начале координат расположена
устойчивая особая точка типа центра.
.
Фазовые траектории имеют вид эллипсов
с центром в начале координат (см. рис.
5.30). В начале координат расположена
устойчивая особая точка типа центра.
![]()





![]()
Рис. 5.30
Если
![]() ,
то корни (5.98) – вещественные, и процессы
в системе – апериодические. Здесь
возможны три случая:
,
то корни (5.98) – вещественные, и процессы
в системе – апериодические. Здесь
возможны три случая:
-
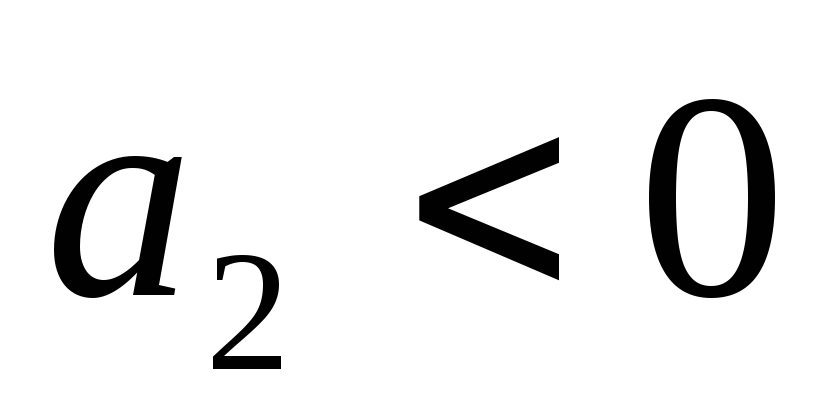 ,
,
 - любое, корни
- любое, корни
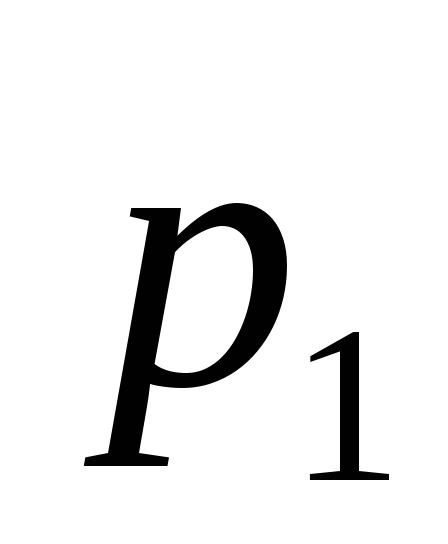 и
и
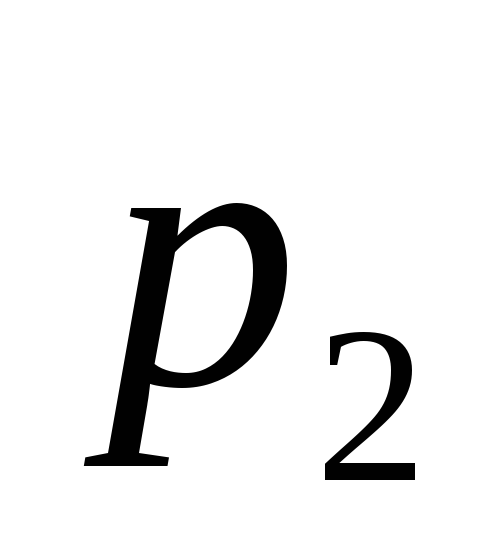 из (5.98) - вещественные и имеют противоположные
знаки. Характер фазовых траекторий
вблизи особой точки, расположенной в
начале координат, показан на рис. 5.31,
а. Эта особая точка – неустойчивая, и
называется седлом.
из (5.98) - вещественные и имеют противоположные
знаки. Характер фазовых траекторий
вблизи особой точки, расположенной в
начале координат, показан на рис. 5.31,
а. Эта особая точка – неустойчивая, и
называется седлом. -
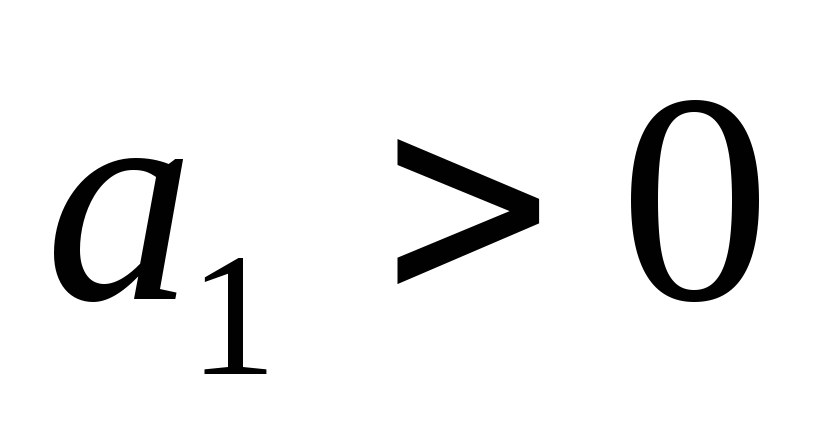 ,
,
 ,
корни
,
корни
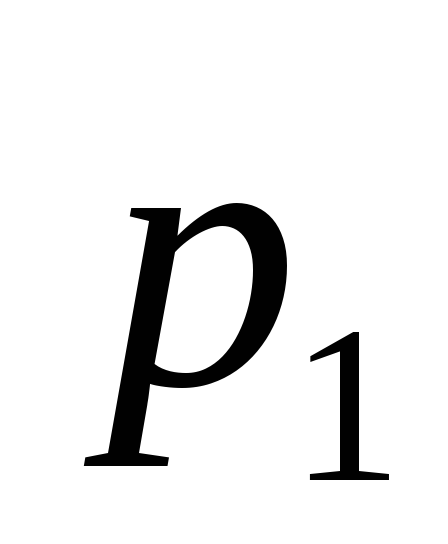 и
и
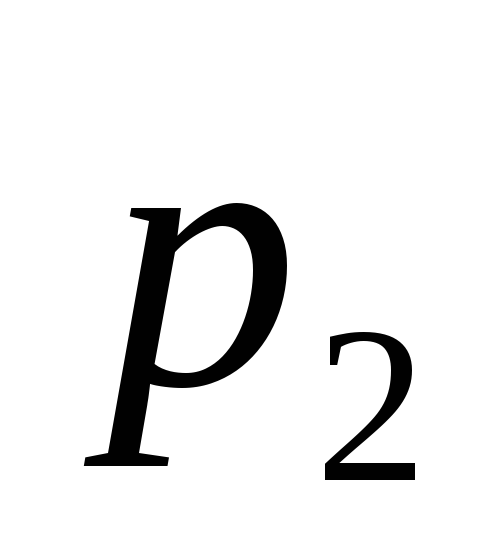 из (5.98) – вещественные и отрицательные.
Характер фазовых траекторий вблизи
особой точки, расположенной в начале
координат, показан на рис. 5.31, б. Эта
особая точка – устойчивая, и называется
устойчивым узлом.
из (5.98) – вещественные и отрицательные.
Характер фазовых траекторий вблизи
особой точки, расположенной в начале
координат, показан на рис. 5.31, б. Эта
особая точка – устойчивая, и называется
устойчивым узлом. -
 ,
,
 ,
корни
,
корни
 и
и
 из (5.98) – вещественные и отрицательные.
Характер фазовых траекторий вблизи
особой точки, расположенной в начале
координат, показан на рис. 5.31, в. Эта
особая точка – неустойчивая, и называется
неустойчивым узлом.
из (5.98) – вещественные и отрицательные.
Характер фазовых траекторий вблизи
особой точки, расположенной в начале
координат, показан на рис. 5.31, в. Эта
особая точка – неустойчивая, и называется
неустойчивым узлом.









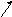

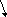
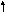


![]()
![]()








![]()
Рис. 5.31
В случае нелинейных дифференциальных уравнений исследование характера фазовых траекторий вблизи особых точек совпадает с исследованием устойчивости состояний по Ляпунову. Тогда нелинейная система, описываемая дифференциальным уравнением второго порядка, для малых отклонений от состояния покоя заменяется линейной. Особые точки для линейных уравнений уже были изучены.
Предельные циклы. Замкнутые фазовые траектории, соответствующие возможным периодическим колебаниям, называются предельными циклами. Предельный цикл, от которого прилегающие фазовые траектории с течением времени удаляются, называется неустойчивым, а к которому приближаются, накручиваясь на него - неустойчивым. В реальных системах могут существовать только устойчивые предельные циклы. В нелинейных системах обычно бывает небольшое число предельных циклов – один или два. Для определения их положения может оказаться полезным метод кольца.
5.14. Генерирование несинусоидальных колебаний
Области применения генераторов негармонических колебаний определенной формы разнообразны: многоканальные системы связи, вычислительные и измерительные устройства, радиолокация и т.д. Например, в осциллографах и телевизорах применяются генераторы пилообразного напряжения для осуществления развертки. В импульсных устройствах – генераторы прямоугольных, треугольных или другой формы импульсов. Генераторы релаксационных колебаний создают в релаксационных устройствах колебания, функция или производная которых терпит разрыв.
Релаксационные генераторы. Они могут быть реализованы на основе схем генераторов гармонических колебаний при определенном выборе параметров этих схем. Существуют также специальные схемы релаксационных генераторов, преимущественно - на транзисторах, диодах, электронных лампах, магнитных элементах и их комбинациях. Возьмем схему транзисторного генератора (см. рис. 5.6). Нелинейное уравнение автогенератора:
![]() (5.46)
(5.46)
где
![]() - сеточное напряжение,
- сеточное напряжение,
![]() - ВАХ нелинейного элемента - транзистора,
- ВАХ нелинейного элемента - транзистора,![]() - резонансная частота высокодобротного
колебательного контура в генераторе,
- резонансная частота высокодобротного
колебательного контура в генераторе,
![]() .
.
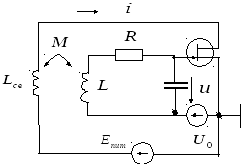
Рис. 5.6
Для
генератора, работающего в мягком режиме
возбуждения, аппроксимируем ВАХ
нелинейного элемента относительно
рабочей точки как
![]() .
Это выражение подставим в (5.46), получим
уравнение:
.
Это выражение подставим в (5.46), получим
уравнение:
![]() (5.100)
(5.100)
где
![]() ,
,
![]() .
.
Для придания большей
общности уравнению (5.100) введем обозначения:
![]() ,
,
![]() ,
и безразмерное время
,
и безразмерное время
![]() ,
имеющее смысл фазы колебаний. Вместо
(5.100) получим уравнение Ван-дер-Поля:
,
имеющее смысл фазы колебаний. Вместо
(5.100) получим уравнение Ван-дер-Поля:
![]() (5.101)
(5.101)
Если
![]() ,
то (5.101) описывает гармонические колебания
с фазовыми траекториями на фазовой
плоскости
,
то (5.101) описывает гармонические колебания
с фазовыми траекториями на фазовой
плоскости
![]() в виде концентрических окружностей или
эллипсов. Чем меньше параметр
в виде концентрических окружностей или
эллипсов. Чем меньше параметр
![]() ,
тем колебания по форме ближе к
гармоническим. Плавно увеличивая
значение
,
тем колебания по форме ближе к
гармоническим. Плавно увеличивая
значение
![]() ,
можно перейти от гармонических колебаний
к колебаниям, резко отличным по форме
от гармонических. На фазовой плоскости
им соответствуют предельные циклы,
форма которых резко отличается от
окружностей или эллипсов.
,
можно перейти от гармонических колебаний
к колебаниям, резко отличным по форме
от гармонических. На фазовой плоскости
им соответствуют предельные циклы,
форма которых резко отличается от
окружностей или эллипсов.
Генераторы на туннельных диодах. Рассмотрим генератор на туннельном диоде (см. рис. 5.16).

Рис. 5.16
Дифференциальное
уравнение для переменной составляющей
напряжения на
![]() :
:
![]() (5.29)
(5.29)
где
![]() - ВАХ ТД,
- ВАХ ТД,
![]() .
.
Аппроксимируем
ВАХ ТД полиномом
![]() .
Введем безразмерное время
.
Введем безразмерное время
![]() ,
где
,
где
![]() ,
обозначения
,
обозначения
![]() и
и
![]() ,
(5.102)
,
(5.102)
новую переменную
![]() .
Тогда вместо (5.29) получаем уравнение
.
Тогда вместо (5.29) получаем уравнение
![]() (5.103)
(5.103)
где
![]() (5.104)
(5.104)
Из
(5.102) и (5.103) следует, что при
![]() для усиления степени отклонения колебаний
от гармонических надо увеличивать
отношение
для усиления степени отклонения колебаний
от гармонических надо увеличивать
отношение
![]() .
Обычно это достигается путем увеличения
индуктивности.
.
Обычно это достигается путем увеличения
индуктивности.
Уравнение (5.29) равносильно системе
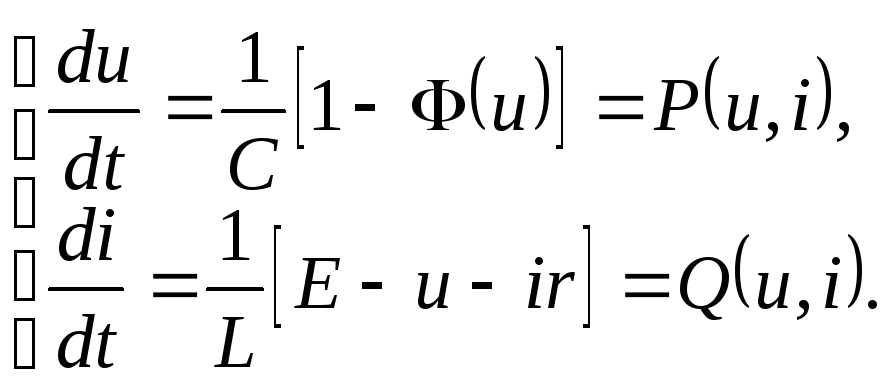 (5.105)
(5.105)
Рассмотрим
на фазовой плоскости
![]() релаксационные колебания. Направление
касательных к фазовым траекториям, как
следует из (5.105),
релаксационные колебания. Направление
касательных к фазовым траекториям, как
следует из (5.105),
![]() (5.106)
(5.106)
При
больших значениях
![]() траектории почти горизонтальны (
траектории почти горизонтальны (![]() )
всюду, кроме точек фазовой плоскости,
находящихся вблизи зависимости
)
всюду, кроме точек фазовой плоскости,
находящихся вблизи зависимости
![]() .
В таких точках
.
В таких точках
![]() .
Эта зависимость образует изоклину
вертикальных касательных. Предельный
цикл
.
Эта зависимость образует изоклину
вертикальных касательных. Предельный
цикл
![]() ,
получающийся при условии
,
получающийся при условии
![]() ,
показан на рис. 5.32.
,
показан на рис. 5.32.

![]()
![]()
![]()
![]()







![]()


![]()
![]()
![]()







![]()
![]()
![]()
![]()
![]()
