акустика / nagaenko_av_pezoelektricheskie_preobrazovateli

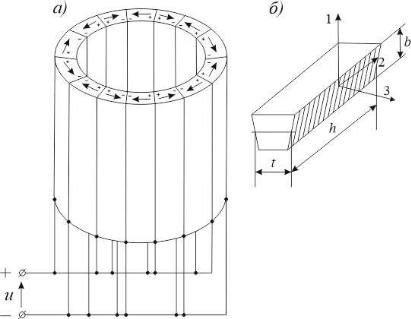
Сегментированный (составной/наборный) цилиндрический

преобразователь. С целью увеличения эффективности цилиндрических преобразователей или сложности изготовления цилиндров больших размеров их изготавливают из отдельных частей (сегментов), склеенных друг с другом и имеющих одинаковые размеры. Составной цилиндр и его отдельный сегмент представлены на рис. 18. При таком исполнении цилиндра его электроды нанесены не на образующие поверхности как при монолитном исполнении, а располагаются боковых поверхностях единичного элемента

(призмы). При параллельном соединении призм преобразователь работает на продольном пьезоэффекте, т.е. приложенное по оси 3 внешнее электрическое поле ориентированно по средней окружности цилиндра, т.о. совершая радиальные колебания.

Упругие характеристики наборного цилиндра аналогичны характеристикам монолитного и обладают равными реактивными механическими сопротивлениями, а активное сопротивление наборного цилиндра больше монолитного ввиду потерь, возникающих в местах склейки сегментов.

Рис. 18. Сегментированное пьезокерамическое кольцо (а) и отдельная призма (б) [4]

61

Из-за малого угла скоса в основании призмы ее сечение можно принять

за прямоугольное, тогда напряженность электрического поля 3 = ⁄, где t

– межэлектродное расстояние призмы, измеренное по ее средней линии.

Напряженность электрического поля 3 провоцирует в пьезоэлектрике механическое напряжение 3 и силу 3 благодаря обратному пьезоэффекту,

которые равны 3 = −(33⁄33) 3 и 3 = 3 . Результирующая радиальная упругая сила Fr, как и в монолитном цилиндре, в 2π раз превышает нормальную

цилиндра nс в 33⁄31 раз больше коэффициента трансформации n

монолитного цилиндра. Поскольку продольный пьезомодуль 33

приблизительно в два раза больше поперечного 31 практически для всех пьезокерамических материалов и отношение ⁄ можно изменять, то получается, что nс в несколько раз превышает n.

Отсюда следует, порядок расчета и приведенные формулы,

описывающие работу монолитного цилиндрического преобразователя справедливы и для составного цилиндра (приложение 3) при замене n на nc.

Заданная акустическая мощность в сегментированном преобразователе достигается при напряжении в nс/n раз меньше, чем в монолитном.

62

Стоит отметить, что механическая прочность сегментированных цилиндров уступает монолитным, в связи с чем их упрочняют предварительным постоянным сжатием.

Сферический преобразователь

Принцип действия и эквивалентные параметры сферического

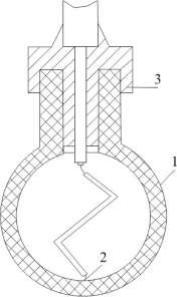
преобразователя. Преобразователь выполняется в форме сферы 1 (рис. 19)

электроды, которого расположены на его внешней и внутренней поверхностях, т.о. сфера наполяризованна по толщине. Токовывод 2 от внутренней части сферы выходит через отверстие в ее оболочки и сальник 3.

Рис. 19. Сферический пьезокерамический преобразователь [4]

Если к оболочке пьезокерамической сферы со средним радиусом а и

толщиной δ, при условии, что приложить переменное электрическое напряжение u с напряженностью поля 3 = ⁄, то в ней возбудятся колебания с амплитудой в направлении ее радиуса, т.е. радиальные колебания. При этом любая из точек сферы будет испытывать одинаковую деформацию равную ⁄, а площадь поверхности сферы изменится на величину 2ξr/а.

Т.о. расчет колебаний, совершаемых сферой, может быть решен по аналогии с монолитным кольцом. Следуя последовательности определения

63

параметров пьезокерамического кольца получим, что собственная частота 0

свободной от внешних нагрузок сферы определяется выражением

материала, из которого изготовлена сфера.

По аналогии были рассчитать и остальные эквивалентные параметры пьезокерамической сферы

= 4 2 ; = 1⁄4 ;

пьезокерамической сферы. Нагрузку на сферическую оболочку пьезокерамического преобразователя водной среды в электромеханической схеме можно учесть если соколеблющуюся массу воды и активное сопротивление излучения включить параллельно с элементами ее механической стороны (рис. 17).

Ввиду отклонения звуковой волны от направления распространения

(дифракции) на поверхности сферы сила F действующая на ее оболочку будет различной. Разность потенциалов создаваемая звуковой полной в следствии пьезоэффекта на выходе преобразователя, а также и его чувствительность будут задаваться рассеянной звуковой волной. Коэффициент дифракции сферической оболочки д

где р – звуковое давление в падающей волне; rва – волновой аргумент для окружающей сферу воды.

Пьезокерамические сферы чаще используют для изготовления преобразователей, работающих в режиме приема. Поэтому приведем только

64

формулу чувствительности пьезокерамического преобразователя в режиме приема, активный элемент которого, выполнен в виде сферы

Пластинчатые преобразователи

Пластинчатыми электроакустическими преобразователями называют

такие преобразователи, у которых механические колебательные системы выполнены в виде пластин круглой или прямоугольной формы. При работе пластинчатых преобразователей как в режиме излучения, так и в режиме приема используются колебания плоской поверхности пластины,

соприкасающейся с водной средой, в направлении своей нормали.

Возбуждаемые колебания пластины могут быть либо продольными (по толщине), либо поперечными изгибными.

Параметры пьезоэлектрического преобразователя с активным элементом в виде пьезоэлектрической пластины и электродами на больших гранях, размеры которой (длина и ширина) велики по сравнению с ее толщиной рассчитывают по формулам полуволнового стержня.

Для излучения (и приема) низкочастотных колебаний колебательные системы должны быть неприемлемо больших размеров. Так, например,

полуволновой стержень из пьезокерамики ЦТБС-3 при частоте 0 = 500 Гц

имел бы длину = ⁄(2 0) = 3200⁄1000 = 3,2 м, а пьезокерамическое кольцо – = ⁄( 0) ≈ 2м. В целях уменьшения резонансных размеров используют пьезокерамические пластины, совершающие поперечные колебания изгиба.

В электроакустике широко применяют пластинчатые колебательные системы, названные биморфными. Биморфный элемент состоит из двух

65

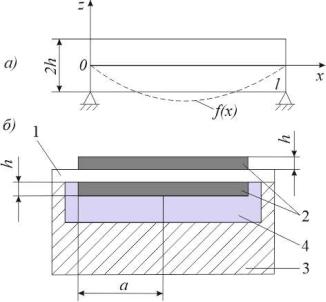
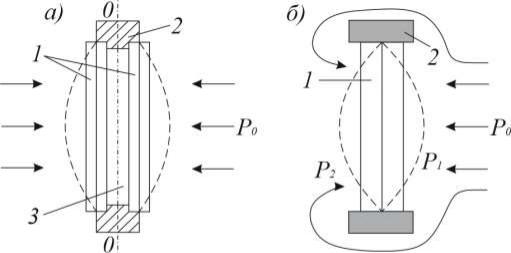
склеенных между собой пьезокерамических пластин, которые свободно опираются по периметру на основании (рис. 20 а). Т.к. направление деформации определяется полярностью прикладываемого электрического поля, то элементы в биморфе можно расположить так, что они будут испытывать различную деформацию, один растягивается, а другой при этом сжимается, т.е. биморф будет изгибаться (рис. 20 а). При механическом воздействии на поверхности пластин, возникают колебания изгиба,

вызывающие электрические заряды на электродах.

Рис. 20. Биморфный элемент (а), состоящий из двух пьезокерамических пластин, и дисковый пластинчатый преобразователь с биморфными пьезокерамическими пластинами (б) [6]

Благодаря использованию поперечных изгибающих колебаний удается изготавливать миниатюрные колебательные системы. Примером такого малогабаритного преобразователя является дисковый пластинчатый преобразователь представленный на рис. 20 б, где 1 – металлический диск, к

которому с двух сторон приклеены дисковые пьезокерамические биморфы 2,

полученная колебательная система размещается в корпусе 3 таким образом,

чтобы один из биморфом помещался в заливочную массу 4. Резонансная

66

частота такого преобразователя, приблизительно равна 800 Гц при а=1 см и

2h= 1 см [9].

Пластинчатые преобразователи, работающие на колебаниях

изгиба. С целью создания изгибных колебаний в преобразователе,

работающем в режиме излучения нужно возбудить изгибающие моменты в поперечных сечения пьезокерамических пластин. Для работы преобразователя в режиме приема элементы в биморфе необходимо соединить так, чтобы изгибные деформации вызывали механические напряжения, которые бы преобразовывались в электрический сигнал на выходе преобразователя.

Приведенным критериям соответствуют колебательные системы,

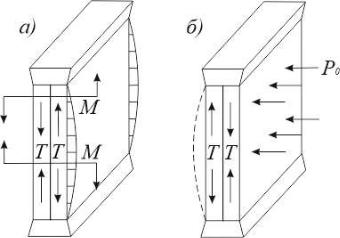
состоящие из жестко связанных разнородных пластин с различными электрическими и механическими характеристиками, которые образуют биморф. Другими словами, в одной пластине должны создаваться напряжения сжатия Т, а другая при этом должна растягиваться, тогда в биморфе возникают изгибающие моменты М (рис. 21 а).

Рис. 21. Схема конструкции пластинчатых преобразователей, работающих на колебаниях изгиба [4]

В случае приемника звуковая волна действует на биморф с давлением

Р0, зафиксированный в опорах биморф изгибается, вследствие чего в

67

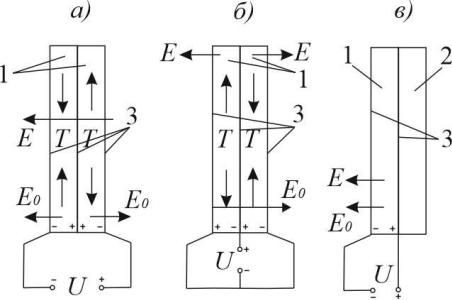
пластинах возбуждаются механические напряжения Т, которые на выходе преобразователя превращаются в электрический сигнал (рис. 21 б).

Для эффективной работы пластинчатых пьезоэлектрических преобразователей пластины в биморфном элементе необходимо соединять в определенной последовательности.

Различные характеристики пьезокерамических пластин можно создать выбором взаимных направлений полей первоначальной поляризации (вектор

Е0) и прикладываемого электрического (вектор Е). Если вектора Е0 и Е одной из пластин соноправлены, то в ней действуют механические напряжения (Т) в

одном направлении, а в это время в соседней пластине эти вектора направлены во встречных направлениях, т.о. создавая в ней механические напряжения противоположного направления (рис. 22 а, б). Описанным

«противодействием» двух пластин объясняется возникновение изгибающего момента в их поперечных сечениях

Рис. 22. Последовательное (а) и параллельное (б) соединение пластин в биморфных элементах, полупассивная колебательная система (в) [4]

В случае, когда биморфный элемент изготовлен из пластин, одна из которых выполнена из пьезокерамического материала 1, а другая из пассивного 2 (металл, диэлектрик и т.д.) изгибающий момент создается

68

внешним электрическим полем или деформацией в активной пластине, а

пассивная при этом не меняет свои геометрические размеры. В случае воздействия на такой преобразователь звуковой волны изгибные деформации пьезоактивной пластины провоцируют в ней механические напряжения,

которые в результате прямого пьезоэффекта преобразуются к появлению зарядов на его электродах 3. Описанная колебательная система получила название полупассивной.

Для достижения максимальной эффективности пластинчатых преобразователей биморфный элемент фиксируют таким образом, чтобы условия его закрепления приближались к свободному опиранию краев. С этой целью преобразователи выполняют симметричными (рис. 23 а) из двух объединенных в одной конструкции биморфных элементов 1, которые располагают соосно параллельно друг другу на несущей их опоре 2 с

небольшими воздушным промежутком 3 между ними, играющим роль экрана.

Здесь используют осесимметричные колебания, возникающие при движении биморфных элементов в противоположных направлениях относительно плоскости симметрии ОО; форма колебаний показана штрихами.

Рис. 23. Схема соединения биморфных элементов в преобразователе [4]

По такой конструктивной схеме, как правило, выполняют и преобразователи-излучатели, и преобразователи-приемники давления.

Акустические давления действуют на наружные поверхности обоих

69

биморфных элементов и вызванные ими механические напряжения

преобразуются в электрический сигнал на выходе, пропорциональный давлению.

Резонансные частоты пластинчатых преобразователей.

Резонансные частоты пластинчатых преобразователей foi определяют геометрическими соотношениями, упругими постоянными материалов биморфных элементов и условиями их закрепления:

где 2h – толщина биморфного элемента; l – длина элемента; – собственное число, определяемое условиями закрепления элемента; сизг– скорость распространения поперечных (изгибных) колебаний в материале биморфного элемента.

Из формулы (81) видно, что резонансные частоты пластинчатых изгибных преобразователей пропорциональны толщине и обратно пропорциональны квадрату длины элемента, причем l всегда в несколько раз больше 2h. Это обстоятельство позволяет выполнять низкочастотные пластинчатые преобразователи малых размеров.

Использование поперечных колебаний изгиба биморфных элементов в пластинчатых преобразователях приводит к тому, что длины волн, на которых они работают, всегда значительно больше, чем размеры преобразователей. В

данном случае рабочие поверхности слабо нагружены средой, внутреннее сопротивление преобразователей не согласованно с акустической нагрузкой,

следовательно, они не эффективны в качестве одиночных излучателей,

поэтому чаще их используют в режиме приема. Наиболее эффективно такие преобразователи работают в диапазоне частот, верхняя граница которого может быть приближенно определена условием 2h≤0,1d (l), где d – диаметр; l – длина. Если такое условие не выполняется, т.е. элементы становятся относительно толстыми и, как следствие, жесткими, деформации изгиба уменьшаются и эффективность преобразователей падает. При этом

70