
лекции / DSP_1
.pdf
1
Лекция 1. Введение в ЦОС
1.ЦОС — что это такое?
2.Основные типы сигналов.
3.Типовые дискретные сигналы.
4.Нормирование частоты.
5.Основная полоса частот.
6.Обобщенная схема ЦОС.
1.1. ЦОС – что это такое?
ЦОС — это обработка цифровых сигналов средствами цифровой вычислительной техники.
ЦОС — типичный пример науки на стыке наук:
дискретная математика;
вычислительная техника;
теория цепей;
радиотехника.
Кратко технологию ЦОС можно сформулировать так:
идея метода цифровой обработки сигнала;
математическая модель;
алгоритм;
компьютерное моделирование;
программный продукт (soft product);
его реализация на цифровом вычислительном устройстве (hard product).
Для того чтобы овладеть этой технологией необходимо получить знания в следующих областях:
1.Фундаментальная теория ЦОС (базовые методы и алгоритмы), инвариантная относительно физической природы сигнала.
2.Компьютерное моделирование ЦОС.
3.Реализация алгоритмов ЦОС на ЦСП, ПЛИС и т.п.
4.Приложения цифровой обработки (пп. 1—3) для сигналов конкретной физической природы (аудио, видео и т. д.).
В рамках базового курса ЦОС изучаются разделы 1—2.
1.2. Основные типы сигналов
Сигнал — это физический процесс, несущий в себе информацию.
Аналоговый сигнал — это сигнал, непрерывный по времени и по состоянию (уровню).
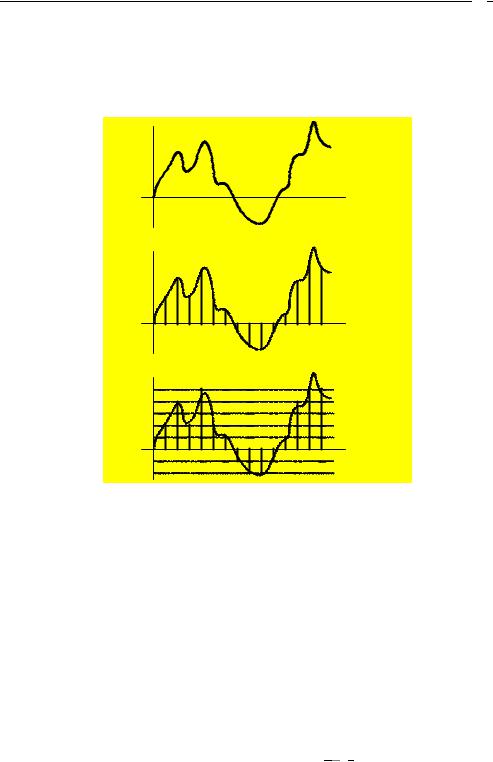
Описывается непрерывной или кусочно-непрерывной функцией x(t) (рис. 1.1, а).
Дискретный сигнал — это сигнал, дискретный по времени и непрерывный по состоянию (уровню).
Описывается последовательностью чисел бесконечной разрядности x(nT) или x(n), которую называют коротко последовательностью (рис. 1.1, б).
Значения nT |
называют |
дискретным |
временем, где |
T |
1 |
— |
период |
|||
|
||||||||||
|
|
|
|
|
fд |
|
|
|
||
дискретизации, |
а n — |
дискретным |
нормированным |
временем |
n |
nT |
|
|||
T |
||||||||||
(тождественно T 1): |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
x(nT) x(n). |
|
|
|
(1.1) |
||||
В теории ЦОС термины "дискретный сигнал" и "последовательность" употребляют в тождественном смысле!
|
|
2 |
Значения x(nT) называют отсчетами. |
|
|
Цифровой сигнал — это сигнал, дискретный по времени и квантованный по |
||
состоянию (уровню). |
|
|
Описывается последовательностью чисел конечной |
разрядности — квантованной |
|
|
|
|
последовательностью x(nT) или |
x(n) (рис. 1.1, в). |
|
x(t) |
|
а |
|
|
|
|
|
t |
x(nT) |
|
б |
|
|
|
|
|
nT |
|
|
|
x(nT) |
|
в |
|
|
|
|
|
nT |
Рис. 1.1. Типы сигналов: а) аналоговый; б) дискретный (последовательность); в) цифровой |
||
(квантованная последовательность) |
||
1.3. Типовые дискретные сигналы
Рассматриваемые сигналы будут использоваться далее, пока их перечислим. 1. Цифровой единичный импульс:
|
|
|
|
|
|
|
|
|
|
|
u (n) 1, |
n 0; |
(1.2) |
||||||||||||
0 |
0, |
n 0. |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Цифровой единичный импульс u0(n) |
в ЦОС является аналогом δ-импульса |
||||||||||||||||||||||||
(t) в теории аналоговых систем, |
но |
в |
отличие него, является |
физически |
|||||||||||||||||||||
реализуемым сигналом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
u0(n) |
|
|
|
|
|
|
|
|
|
u0(n m) |
|
m 2 |
|
|
||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 0 1 2 3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 0 1 2 3 |
|
|
|||||||||||||||||||
|
а |
|
б |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.2. Цифровой единичный импульс: а) не задержанный; б) задержанный
Цифровой единичный импульс, задержанный на m периодов дискретизации:
u (n m) 1, |
n m; |
(1.3) |
0 |
n m. |
|
0, |
|

3
Фильтрующее свойство цифрового единичного импульса подобно фильтрующему свойству δ-импульса (свертка сигнала с δ-импульсом):
|
|
|
|
|
|
|
|
|
x(t) x( ) (t ). |
|
|
|
|
0 |
|
|
|
При замене |
|
и mT переходим к свертке дискретного сигнала с |
|||
t nT |
|||||
цифровым |
единичным |
импульсом (конволюция): |
|
||
|
|
|
|
|
|
|
|
x(nT) x(mT)u0(nT mT). |
|
||
|
|
|
m 0 |
|
|
В области дискретного нормированного времени: |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(n) x(m)u0(n m) |
. |
(1.4) |
|
|
|
m 0 |
|
|
Фильтрующее свойство означает, что из бесконечной последовательности выделяется один отсчет в текущий момент времени n.
Пример 1.1.
Определить, чему равна правая часть (1.4) при n 2.
x(m)u0(2 m) x(0)u0(2) x(1)u0(1) x(2)u0(0) x(3)u0( 1) x(2) .
m 0
2. Цифровой единичный скачок:
|
|
|
|
|
|
|
u (n) 1, n 0; |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, n 0. |
|
|
|
|
|
|
|
|
||
u0 |
(n) |
|
|
|
|
|
u0(n m) |
|
|
|
|
|
|
|
m 2 |
||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 0 1 2 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
1 0 |
1 2 3 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.3. Цифровой единичный скачок: а) не задержанный; б) задержанный
3. Дискретная экспонента:
an, n 0;
x(n) (1.5)
0, n 0.
x(n) x(n)
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
1 |
|
3 |
|
|
5 |
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 0 1 2 3 4 5 |
|
|
1 |
0 |
2 |
4 |
|
|
|||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.4. Дискретная экспонента: а) 0 < a <1; б) а < 0 и | a| <1
4. Дискретный гармонический сигнал:

|
|
|
|
4 |
|||
Аналоговый гармонический сигнал: |
|
|
|
|
|||
x(t) Ccos( t) Ccos(2 ft). |
|
|
|
|
|||
Дискретный гармонический сигнал: |
|
(рис. 1.5): |
|
|
|
|
|
t nT |
|
|
|
|
|||
|
|
|
f |
|
|||
x(nT) x(n) Ccos( Tn) Ccos(2 fnT) Ccos 2 |
n . (1.6) |
||||||
|
|||||||
|
|
|
fд |
|
|||
|
|
|
|
||||
C |
|
|
|
|
|||
x(nT) |
|
|
|
|
|||
nT
0
T
Рис. 1.5. Аналоговый (огибающая) и дискретный гармонические сигналы
5. Дискретный комплексный гармонический сигнал: |
|
||||
Аналоговый комплексный гармонический сигнал: |
|
||||
|
x(t) Ce j t . |
|
|||
Дискретный комплексный гармонический сигнал |
|
: |
|
||
t nT |
|
||||
|
|
. |
|
||
|
x(n) Cej Tn |
(1.7) |
|||
Физически — это два сигнала:
x(n) Ccos( Tn) jCsin( Tn).
1.4. Нормирование частоты
Пример 1.2
Записать две дискретные гармоники (1.6) при следующих исходных данных:
1. |
C 1; |
f |
2Гц; |
fд 16 Гц : |
|
|
|
|
|
|
x(n) cos |
|
n . |
|
|
|
|
|
||
|
|
|
|
4 |
|
|
2. |
C 1; |
f |
5кГц; |
fд 40кГц : |
|
|
x(n) cos n .4
Выводы:
1.Получены одинаковые гармонические сигналы, т.к. в них имеем одинаковое
отношение f . fд
2.По этой причине в ЦОС, помимо абсолютных частот f (Гц) и ( рад/с)
используются нормированные частоты:
|
|
|
|
|
f |
|
|
|
f |
|
|
|
|
(безразмерная); |
|
|
|
fд |
|
||||
|
|
|
|
|
|
||
|
|
|
T (рад). |
|
|||
|
|
|
|
(1.8) |
|||
|
|
|
|||||
fд

5
Нормированная частота широко используется в теории ЦОС, а нормированная
частота f — при моделировании в MATLAB.
1.5. Основная полоса частот
Согласно теореме Котельникова, точное восстановление аналогового сигнала с финитным спектром, ограниченным частотой fв , гарантируется при выборе частоты дискретизации fд из условия:
fд 2 fв ,
поэтому вещественный дискретный сигнал и характеристики системы, его
обрабатывающей, анализируют на интервале |
|
|
||||
|
0; |
fд |
|
0; f |
, |
(1.9) |
|
2 |
|||||
|
|
|
в |
|
||
которую называют основной полосой частот.
Основная полоса в шкале частот :
|
д |
|
|
|
|
|
|
|
|
0; |
|
|
|
|
0; |
|
. |
||
2 |
0; fд |
|
|||||||
|
|
|
|
|
|
|
T |
||
Основная полоса в шкале нормированных частот : |
|
|||
|
0; |
. |
(1.10) |
|
|
|
|
|
|
Пример 1.3 |
|
|
|
|
Заданы частота дискретизации fд 10кГц и частота гармоники |
fд 2кГц. |
|||
1. Записать основную полосу частот в шкалах f и . |
|
|||
2.Определить частоту гармоники в шкале .
Основная полоса частот: f 0;5 (Гц)
0; (рад).
Частота гармоники f 2кГц в шкале определяется на основании взаимосвязи:
|
f |
|
|
|
fд |
|
||||
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
f |
|
||||
|
|
|
|
|
|
|
. |
(1.11) |
||
|
fд |
2 |
||||||||
|
|
|
|
|
||||||
В примере: |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
(рад). |
|
|||
5 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
6
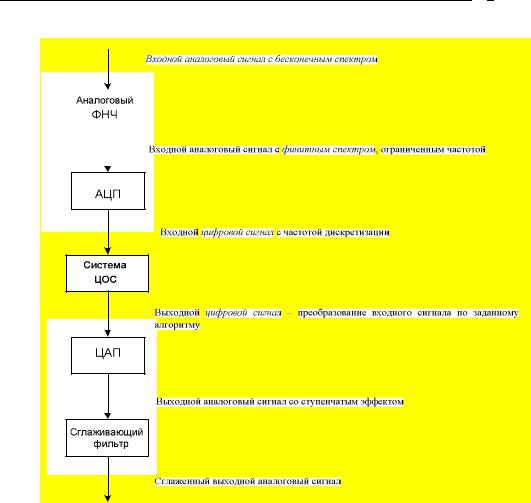
1.6. Обобщенная схема ЦОС
x(t)
|
|
fв |
|
|
|
x(t) |
|
|
|
fд 2fв |
x(nT) |
y(nT)
y(t)
y(t)
Рис. 1.6. Обобщенная схема ЦОС
ЦОС в реальном времени означает, что алгоритм обработки сигнала выполняется в темпе поступления отсчетов, т. е. за период дискретизации T .
