§ 6. Неинерциальные системы отсчета.

Силы инерции при ускоренном (с ускорением ) поступательном движении системы отсчета:.

Сила Кориолиса:. В случае вращающейся системы отсчета силу инерции называют центробежной силой. ,- центростремительное ускорение. На движущееся со скоростьюво вращающейся системе отсчета тело действует также сила Кориолиса.

Основной закон динамики для неинерциальных систем отсчета ,- ускорение в неинерциальной системе отсчета.

§ 7. Элементы специальной теории относительности.

Преобразования Лоренца: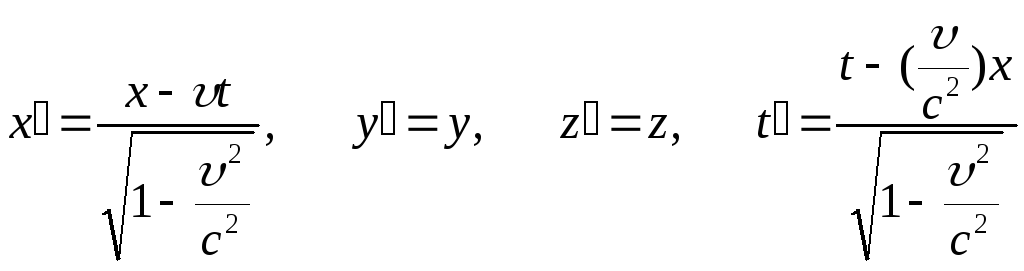, где- скорость света в вакууме. Сокращение длины движущегося тела:, где- длина движущегося тела,- собственная длина. Замедление хода движущихся часов:

, где - интервал времени между событиями в движущейся системе отсчета,- интервал времени между теми же событиями в неподвижной системе.

Релятивистский закон сложения скоростей: 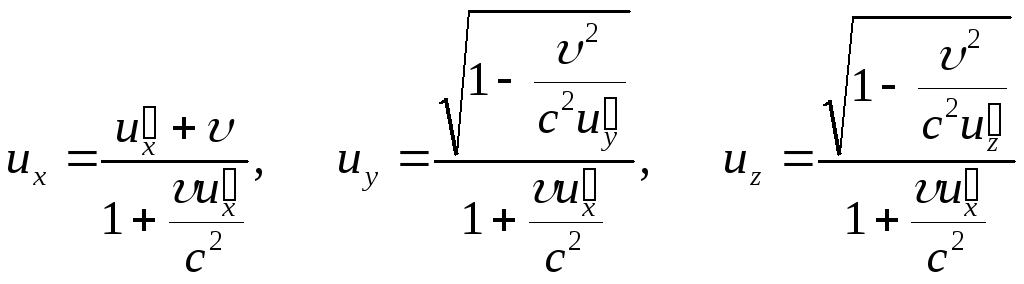, где- проекции скорости в неподвижной системе координат,- проекции скорости в движущейся системе.

Квадрат интервала - между событиями 1 и 2 инвариантная величина:, где- интервал времени между событиями 1 и 2,- расстояние между точками 1 и 2, в которых произошли данные события.

Релятивистская масса и импульс: 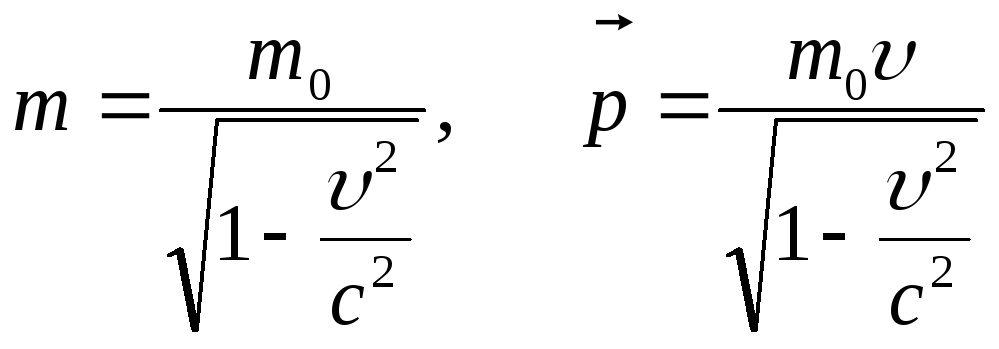, где- масса покоя. Кинетическая энергия движущегося тела:.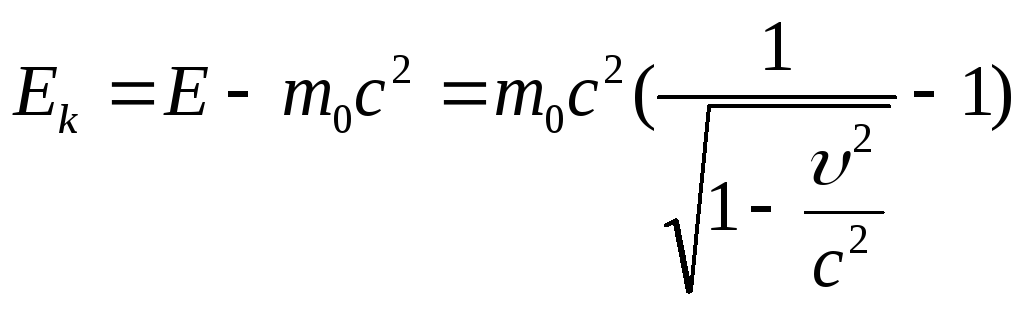

Взаимосвязь массы и энергии 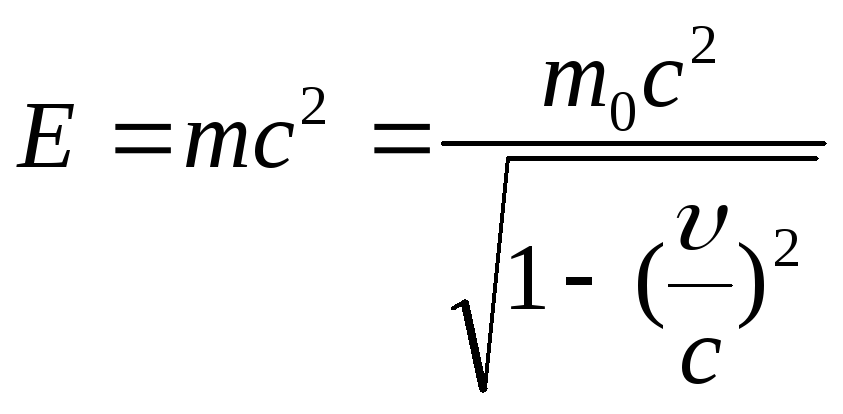, Связь между полной энергией и импульсом релятивистской частицы.

§ 8. Упругие свойства тел.

Относительная продольная деформация:, где- приращение длины при растяжении или сжатии,- длина тела до деформации.

Относительной деформацией кручения называется отношение угла закручивания к длине стержня: .

Относительное изменение объема при продольной деформации: , где- коэффициент Пуассона, равный отношению относительной поперечной деформации к продольной:.

Напряжение при упругой деформации:, где- сила, действующая на сечение.

Зависимость между относительной продольной деформацией и деформирующей силой (закон Гука): , где- коэффициент упругости,- модуль Юнга.

Разрушающая сила: , где- разрушающее напряжение.

Относительное изменение толщины:, где- коэффициент поперечного сжатия при продольном растяжении.

Деформация сдвига характеризуется углом сдвига, определяемым по формуле:

, где - коэффициент сдвига,- сила, вызывающая сдвиг,- касательное напряжение,- модуль сдвига.

Модуль Юнга Е, модуль сдвигаи коэффициент Пуассонасвязаны соотношением:. Угол закручивания стержня:, где- вращающий момент,- длина стержня,- радиус стержня.

Потенциальная энергия упруго деформированного стержня:, где- объем стержня. Плотность энергии упруго деформированного стержня:.

§ 9. Механические колебания и волны.

Уравнение затухающих колебаний и его решение: , где- коэффициент затухания,- частота затухающих колебаний:. Логарифмический декремент затухания:. Период малых колебаний математического маятника:, где- длина маятника,- ускорение силы тяжести. Период колебаний тела, подвешенного на пружине:, где- масса тела,k- жесткость пружины. Период малых колебаний физического маятника:, где- приведенная длина физического маятника,- момент инерции маятника относительно оси качания,- масса маятника,- кратчайшее расстояние от центра масс до оси качания. Амплитуда вынужденных колебаний при действии вынуждающей силы:гдеи- частоты собственных колебаний при отсутствии затухания и вынуждающей силы. Период колебаний однородной струны:, где- длина струны,- масса единицы длины струны,- сила натяжения струны.

Полная энергия материальной точки массой , которая совершает гармонические колебания:. Скорость распространения волны:, где- длина волны. Скорость распространения продольных волн в тонких стержнях:, где- модуль Юнга среды,- плотность материала стержня.

Скорость распространения поперечных волн: ,где- модуль сдвига.

Скорость продольных волн в неограниченной упругой среде:, где- модуль всестороннего сжатия.