Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

FTT_Sadykov_5

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

613.27 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

5. Колебания кристаллической решетки.

Поступательное движение атомов в кристалле подавлено. В то же время атомы могут совершать колебательное движение около своих положений равновесия. Этим движением объясняется целый ряд свойств твердых тел.

Динамика решетки.

Введем Uls - смещение s - ого атома l - ой элементарной ячейки решетки. Тогда

кинетическая энергия и потенциальная энергия, определяющие колебательное движение кристалла, выражаются как (i, j – декартовы составляющие смещения, Ms- масса атома):

Eкин

M s U

Vпот

пот

, .

Uls

Uls 0

l s

Для положений равновесия (Ulsi 0 ) второе слагаемое равно нулю. Запишем

уравнения движения (Лагранжа) и преобразуем их, вводя очевидные обозначения.

M sU

пот

,s, ,

Uls 0

,s, j, U

M sU

,s, U

,s, ,

lsl

,s,

, Gss, h ,

h l ' l ,

sls

M sUls Gss, h Us,h l . s,h

(5.1)

(5.2)

Решение этого уравнения для l - узла выразим через решение нулевого узла согласно теореме Блоха.

t eiql U0sq t ,

(5.3)

M seiq

0sq Gss, h eiqh eiql U0s,q ,

eiqh ,

M sU0jsq G jj,,

q U j, ,

0s q

0 ,

0sq

e i tU

jj,, q 2M s

, U

, 0 .

(5.4)

s q

s, j,

В приведенных соотношениях посредством q обозначен волновой вектор, который теперь

идентифицирует коллективные решеточные колебания, как ранее k использовался для обозначения блоховских электронных состояний. Число независимых значений q также равно N – числу элементарных ячеек в кристалле. Из условия разрешимости системы уравнений (5.4) определяется 3s значений частот, соответствующих каждому q (закон

дисперсии для решеточных колебаний). Далее эти общие результаты анализируются для более простых случаев.

Линейный кристалл.

Для анализа характера решеточных колебаний рассмотрим более простой пример,

линейную цепочку атомов с постоянной решетки a. Движение атомов происходит вдоль цепочки, под действием квазиупругих сил, обусловленных их взаимодействием с ближайшими соседями. Уравнение движения для l - ого атома цепочки имеет вид:

mul 2ul ul 1 ul 1 .	(5.5)
Будем искать решения этого уравнения в виде:
ul q u0 t exp iqal u0 exp iwt iqal ,	(5.6)

вводя волновое число q для идентификации возможных решений. Подставляя (5.6) в (5.5)

легко получить, mw2u 2 u		1 cos qa , и далее:
0	0
w2 4 m sin2 qa 2 ,			w q 2 m 1 2	sin qa 2	.	(5.7)

Итак, решения (5.5) действительно имеют вид (5.6), если между частотой и волновым числом q имеется соотношение (закон дисперсии) (5.7). Закон дисперсии – периодическая функция с периодом 2 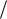a , т.е. она определена в первой зоне Бриллюэна линейного кристалла, см. Рис. 5.1.

Обратим внимание, что выражениями (5.3) и (5.6) вводятся колебательные моды (типы коллективных колебаний); эти моды идентифицируются волновым вектором q (волновым

числом q в одномерном случае). Соотношения (5.3) и (5.6) по существу выражают теорему Блоха. Именно она устанавливает строгую корреляцию между смещениями различных узлов решетки для данного типа колебаний ( q ).

При малых значениях волнового числа закон дисперсии (5.7) упрощается:

w q	qa 0	2 m 1 2 qa	2 v q,	v скорость звука. (5.7’)
	qa 0		s	s

Покажем, что коэффициент перед q в этом выражении действительно равен скорости

звука. К этому выводу можно придти, используем выражение для скорости продольных

звуковых волн в непрерывной среде vs EM 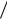, где EM - модуль упругости, -

плотность среды. Чтобы применить эту формулу для дискретной цепочки, введем поперечное сечение цепочки S . Тогда плотность цепочки mSa , а модуль Юнга

(численно равный напряжению при относительной деформации, равной единице) равен

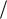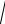
EM aS ; отсюда vs a m . Линейная зависимость (5.7’) хорошо аппроксимирует

закон дисперсии при малых значениях волнового вектора, пунктирная линия на Рис. 5.1.

Смещениями узлов линейной цепочки (5.6) в произвольный момент времени задается мгновенная картина волны, распространяющейся в дискретной среде. Для разных волновых

чисел q эти волны отличаются длиной волны q . Набор возможных значений

волнового числа в пределах 1 ой	зоны Бриллюэна определяется как q 2 n aN , где
N 2 n N 2 , т.е. a q a (к этому результату можно придти в результате тех
же суждений, которые привели нас к выводам (2.15), (2.16) в Разд.2). Таким образом, в
дискретной линейной цепочке	с одним атомом на элементарную ячейку могут

распространяться N волн смещений с длинами волн 2a .

Следующей простейшей моделью колебаний решетки является линейная цепочка с двумя атомами в элементарной ячейке. Смещения атомов атома Ul , ul (с массами М и m,

соответственно) удовлетворяют системе уравнений движения:

MUl 2Ul ul ul 1 ,

mul 2ul Ul Ul 1 .	(5.8)
Решения ищем в виде Ul Aexp iwt iqal ,	ul Bexp iwt iqal , где a -

постоянная решетки. После подстановки этих выражений в (5.8) получаем:

2 Mw2 A 1 e iqa B 0,

1 eiqa A 2 w2m B 0.

(5.9)

Система (5.9) разрешима при равенстве нулю определителя, составленного из ее

коэффициентов. Это определяет возможные частоты колебаний, как решения уравнения:

w4 w2 2 M m

1 e

iqa

0 ,

M m

M m 2

cos2

Mm 2

1,2

Mm 2

M m

2 M m 2

w1,22

sin2

(5.10)

Таким образом,

наше

предположение

о характере колебаний атомов Ul и ul

оправдывается, если закон дисперсии, согласно (5.10), представляет собой двухзначную функцию волнового числа, w1 q и w2 q . Это означает, что теперь, в отличие от одноатомной линейной цепочки, имеется две ветви закона дисперсии, или два типа волн смещений. Зависимости w1 q и w2 q представлены на Рис.5.2., откуда видно, что

каждому значению q (длине волны) соответствуют две частоты,											в частности:
	w	q 0 0 ,		w		q			2 1 2	,		(5.11)
	w	q 0 0 ,		w		q				,		(5.11)
	1				1
							a		M
w	q 0		2 M m	1 2	,		w	q				2	1 2 .	(5.12)
w	q 0				,		w	q					1 2 .	(5.12)
2							2
			mM						a			m

Отличие двух типов волн друг от друга становится очевидным, если определить отношение смещений двух атомов в одной и той же элементарной ячейке. Из (5.9) легко найти, например, пользуясь (5.11) и (5.12):

w1 q0

1 e iqa

q0 1,

2 Mw12 q

w2 q0

1 e iqa

2 Mw22 q

Первый результат означает, что частотная ветвь w1 q в длинноволновой области соответствует колебаниям атомов в элементарной ячейке в унисон, т.е. они колеблются в

одной фазе и с одной и той же амплитудой. Именно так ведут себя звуковые колебания в непрерывной среде. Поэтому w1 q называется акустической ветвью колебаний. Напротив,

для частотной ветви w2 q в пределе q 0 атомы одной элементарной ячейки

колеблются в противофазе, а их амплитуды соотносятся как обратные массы. Такие колебания являются оптически активными, т.е. они являются источником излучения оптических фотонов или могут быть возбуждены внешним оптическим излучением.

Частотная ветвь w2 q называется оптической.

Результаты, полученные для продольных колебаний цепочки, можно обобщить. 1)

Наряду с продольными волнами в цепочке могут распространяться и поперечные волны,

когда смещения атомов происходят перпендикулярно цепочке. Имеется два независимых направления поперечных смещений. Рис. 5.3 представляет законы дисперсии для продольной L и поперечных T1 , T2 волн, распространяющихся в определенном направлении кристалла.

Квантование колебаний решетки.

Колебания линейной цепочки. Смещение l-ого узла цепочки (см. (5.6)) запишем как:

Ul exp iqal u0 exp iw q t exp iqal Qq t ,

где Qq t не зависит от l и	удовлетворяет			уравнению	классического гармонического
осциллятора.
Q		t w2	q Q 0 .		(5.13)
q				q

Задача этого параграфа – ввести квантовое описание гармонического осциллятора.

Рассмотрим наиболее простой случай, описываемый уравнением (5.13), - движение точечной массы под действием упругой силы. Функция Лагранжа этой системы равна:

L T U mx2 x2 , 2 2

классическое уравнение движения этой системы (полученное в соответствие с уравнением

Лагранжа d dL dL 0 ) имеет вид (5.13): dt x dx

x		2 x 0 ,	x 2 x 0 .
	m

В классической механике, такой осциллятор может быть описан также функцией Гамильтона

H		T U	1	p2		1	x2 ,	(5.14)
	кл
		2		m	2

которой в квантовой механике сопоставляется оператор Гамильтона:

1 pˆ

(5.15)

2 m

где

pˆ i

- оператор импульса и

x - безразмерная координата.

Гамильтонианом (5.15) определяется уравнение Шредингера для квантового

осциллятора,

H n

n En n .

(5.15’)

Данное

уравнение

математической

физики

имеет

собственные

значения

En 2n 1

n 1 2 ,

n 0,1,2,3,... и собственные функции n , которые

выражаются через полиномы Эрмита Hn ,

e 2

2 1 n ,

(5.16)

- нормировочный множитель.

Для

n 0

имеем

функцию

основного

состояния

осциллятора 0 и энергию основного состояния осциллятора E0

(нулевую энергию):

m x2

4 e

e 2

(5.17)

В общем случае энергию

состояния n можно интерпретировать как энергию

основного состояния

2 плюс энергию n квантов колебательного движения (фононов),

по

у каждого

кванта.

Это

позволяет

интерпретировать

как n-фононное

колебательное состояние осциллятора. Если ввести операторы aˆ

и aˆ соотношениями:

(5.18)

то их действие на n , как легко проверить, (см. (5.16)) выражается соотношениями

aˆ

n 1

aˆ

n 1

(5.18’)

Т.е. эти операторы переводят n-фононное состояние в состояния с n 1

фононами и n 1

фононами, соответственно. Поэтому их называют операторами рождения и уничтожения

фонона. Действие произведения этих операторов,

nˆ aˆ aˆ , на

, как легко показать на

основании

(5.18’),

сводится

умножению

этой

функции

на число фононов:

aˆ aˆ

nˆ

Поэтому произведение aˆ aˆ (именно в указанном здесь порядке)

называют

оператором

числа

частиц,

nˆ aˆ aˆ .

Пользуясь

определениями (5.18) легко

показать, что

aˆ

1 и гамильтониан (5.15)

можно выразить через оператор nˆ aˆ aˆ :

nˆ

(5.19)

Теперь удобно перейти от координатного представления собственных функций осциллятора к представлению чисел заполнения: n n , где n описывает n -фононное состояние, которое может меняться под действием операторов рождения и уничтожения (см.

(5.18’)):

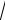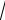aˆ nn 1 n 1 , aˆ nn n 1 .

Через операторы рождения и уничтожения можно выразить и операторы других физических величин, например, из (5.18) легко получить операторы координаты и импульса

для одномерного осциллятора:

xˆ

aˆ aˆ ,

pˆ i

aˆ aˆ . (5.20)

Все, что говорилось об одномерном осцилляторе, применимо для амплитуды

0q t

коллективных колебаний ( Qq в случае линейного кристалла (5.13) и U

в трехмерном

случае, см.(5.3) для s 1).

U0jq 2j q U0jq

0, с поляризациями

j 1,2,3.

(5.21)

В приближении малых колебаний,

состояние кристалла задается совокупностью 3sN

независимых осцилляторов (гармоническое приближение). Оператор смещения и оператор импульса для узла решетки l выражаются через 3N операторов рождения и уничтожения фононов, по аналогии с (5.20), как (монотомная решетка, т.е. s=1):

j aˆqje

iql

U l

aˆqje

2m j q

m j q

j aˆqje

iql

P l

aˆqje

(5.22)

j - единичные векторы поляризации, j =1,2,3.

В общем случае для трехмерного кристалла число осцилляторов будет 3sN , где N –

число волновых векторов q (элементарных ячеек в кристалле), s (число атомов в

элементарной ячейке) определяет число ветвей колебательного спектра, коэффициент 3

учитывает три поляризации для каждой ветви. Каждой колебательной моде qj

( j 1,2,3,..3s ) соответствует своя частота и энергия фонона: qj j q j q .

Закона дисперсии j q , в принципе, определяется решением секулярной задачи (5.4). Выражения для операторов смещения и импульса, аналогичные (5.22), в случае

полиатомной решетки ( s 1) можно найти в [1].

Тепловая энергия колебаний.

Таким образом, в рамках квантовой теории колебательное движение решетки в приближении малых колебаний описывается совокупностью 3sN независимых

осцилляторов. Каждый осциллятор имеет эквидистантный энергетический спектр.

Сосредоточимся теперь на возможных состояниях одного осциллятора. 1) Прежде всего,

осциллятор может находиться в состоянии с определенным числом фононов n (в

координатном представлении это состояние определяется как n ). Однако реализовать состояние с определенным числом фононов весьма трудно. 2) Следующее возможное

состояние -

когерентное состояние осциллятора. Такое состояние

представляется как

линейная

комбинация

состояний

n ,

т.е.

имеет

вид

n ,

cn exp

2 2 n

n 0

n! , где -

комплексное число. Состояние

нормировано на

единицу и

является собственным состоянием

оператора уничтожения,

т.е.

1 и

aˆ . Данному состоянию нельзя приписать определенное число фононов. В то же

время для состояния

можно ввести вероятность обнаружить n - фононное состояние,

n ,

которая

определяется

нормированным

распределением

Пуассона

2 exp

с максимумом

при

свойством

n .

Среднее

значение

энергии

осциллятора

в состоянии

n 0

n 1 2 .

следовательно,

равно

1 2

Квантовые

когерентные состояния максимально точно соответствуют классическим состояниям осциллятора, имеющим определенную фазу, в пределе 2 n . Представление когерентных состояний для осцилляторов сыграло большую роль в развитии теории лазеров

иквантовой оптики (Рой Глаубер, Нобелевская премия по физике 2005 г.).

3)Теперь заметим, что состояния n , являются чистыми квантовомеханическими

состояниями, в отличие от смешанных состояний. Чаще всего, осциллятор в результате обмена энергией с термостатом находится в термодинамически равновесном (смешанном)

состоянии. Это состояние описывается матрицей плотности и характеризуется заселенностями exp En kT n - фононных квантовых (чистых) состояний осциллятора.

Термодинамически средняя энергия осциллятора в этом случае равна:

					n 1 2 , (5.23)
Eосц En exp En kT			exp En	kT	n 1 2 , (5.23)
	n 0		n 0
где En	n 1 2 ,	n 1 exp kT 1 - функция распределения				Бозе-

Эйнштейна.

Переход от термодинамически средней энергии одного осциллятора к энергии колебаний трехмерной решетки осуществляется суммированием средних энергий всех осцилляторов (гармоническое приближение):

реш qj					1
	Eосц qj		j q	nqj		.	(5.24)
					2
		qj

Целесообразно в выражении (5.24) перейти от суммирования к интегрированию, чтобы получить хотя и приближенный, но аналитический результат. Это достигается упрощением закона дисперсии.

Существует несколько моделей для такого упрощения. Модель Эйнштейна исходит из того, что атомы в каждом узле решетки колеблются независимо от колебаний других узлов,

т.е. в этом случае имеется 3sN осцилляторов с одинаковой частотой E (частота

Эйнштейна). Эти колебания локализованы вблизи узлов решетки. В этом случае тепловая энергия кристалла выглядит как:

E	3Ns	E	n	1 2 .
реш		E	E

Однако более реалистичной является модель Дебая, которая уже была рассмотрена

нами выше. Суть этой модели состоит в том, что колебания атомов - коллективные. Поиск решений в виде бегущих волн Uls t eiql U0sq t (см. (5.3)) или ul u0 exp iwt iqal

(см. (5.6)) означает жесткую корреляцию смещений различных узлов между собой для данного типа колебания ( q или q ). Как результат мы получили зависимость частоты

коллективных колебаний от волнового вектора q или от q (длины волны бегущих по цепочке волн). Для облегчения суммирования в (5.24) Дебай сделал несколько радикальных упрощений закона дисперсии. Суть первого упрощения состоит в следующем. Из (5.7)

видно, что для малых волновых чисел закон дисперсии становится линейным:

aq 1

sin

aq v

зв

q .

Дебай предположил линейный закон дисперсии во всем диапазоне изменения волновых

векторов. Для трехмерной решетки с одним атомом в элементарной ячейке это означает, что

	q vi	q	, где i - поляризация колебаний. Об этом соотношении можно говорить как о
	q vi	q
i	зв

законе дисперсии в приближении Дебая. Очевидно, поверхностями постоянной частоты в этом случае являются сферы. Пользуясь законом дисперсии в приближении Дебая, запишем


число	осцилляторов		dzi (поляризации i ), частоты которых заключены в интервале
d (сфере частоты соответствует радиус q , и d q dq ):
dz	V 4 q2dq	gi d , и найдем функцию спектральной плотности для

i	8 3		D

колебаний поляризации i

gDi	V 2		.
	2 2 vзвi	3

Еще большее упрощение достигается, если ввести суммарную по поляризациям спектральную плотность соотношением (l (t) – продольная (поперечная) поляризация звука):

1 / 21 2 > Следующая >>>

Соседние файлы в папке ФТТ_Садыков_2012

#
10.02.2015337.03 Кб20FTT_Sadykov_1.pdf
#
10.02.2015967.18 Кб23FTT_Sadykov_2.pdf
#
10.02.2015409.34 Кб20FTT_Sadykov_3.pdf
#
10.02.2015417.43 Кб20FTT_Sadykov_4.pdf
#
10.02.2015613.27 Кб19FTT_Sadykov_5.pdf
#
10.02.2015553.51 Кб19FTT_Sadykov_6.pdf
#
10.02.2015571.76 Кб18FTT_Sadykov_7.pdf
#
10.02.2015386.84 Кб21FTT_Sadykov_8.pdf
#
10.02.201590.01 Кб20FTT_vvedenie.rtf
#
10.02.2015277.6 Кб21r929c.pdf