Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

FTT_Sadykov_6

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

553.51 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

6. Взаимодействие излучения (электронов, нейтронов,

рентгеновских квантов) с кристаллом.

Условие образования дифракционных максимумов

Рассмотрим в качестве примера рассеяние свободных электронов на кристаллической решетке. В этом случае электрон взаимодействует с кристаллическим потенциалом, который может быть представлен как сумма атомных потенциалов, центрированных в узлах,

положения которых задается Rl :


VCr Va r R		.	(6.1)
VCr Va r R	l	.	(6.1)

l

Введем волновые функции для падающего и рассеянного электрона

k r 1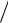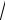V exp ikr i k t , k ' r 1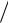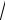V exp ik 'r i k ' t .

Амплитуда перехода электрона из состояния k в состояние k ' (при этом кристалл

переходит из колебательного состояния

в состояние

n '

), равна:

n n,

k k ,

k ' n '

n k

exp i k k ' t exp i n t i n ' t

VCrk k , 0

n , (6.2)

где n - энергия колебательного состояния n . Прежде всего, вычислим матричный

элемент между электронными состояниями:

VCrk k , 0 l V1 exp i k ' k r Va r Rl d 3r


	1		exp iKR		Va K S K Va K . (6.3)

	N			l

			l
Здесь введен вектор		рассеяния K k k				и использовано равенство V Na3 . Таким

образом, необходимый матричный элемент равен произведению структурного и атомного факторов, S K и Va K , соответственно.

	1	exp iKRl ,
S K	1		(6.4)
S K	N		(6.4)

		l

Va K

Va r

Rl exp iK r Rl d 3r .

Далее мы учтем, что положение l - ого узла,

Rl , может быть представлено как сумма

вектора идеальной решетки l

и смещения из положения равновесия Ul

(см. Разд.5).

Rl l Ul .

(6.5)

Смещение Ul согласно (5.22) представляется суммой фононных операторов решетки:

jUqj

exp iql к.с. ,

Uqj Uqj aˆqj

2mN j q

aˆqj .

(6.6)

Перепишем S K

с учетом (6.5), используя выражение (6.6) для U

iKl

S K

exp iK Uqj

exp iql

к.с. ,

Uqj

jUqj aˆqj Uqj aˆqj .

(6.7)

Поскольку Uqj - мало, каждую экспоненту под знаком произведения разложим в ряд

(использовано сокращенное обозначение

Uqj exp iql к.с. Uqj

exp iK Uqj

1 iK Uqj

K Uqj

(6.8)

		ˆ
exp		iK Uqj
qj

	ˆ	1		ˆ	2
1 iK Uqj			K Uqj		.	(6.9)
1 iK Uqj		2	K Uqj		.	(6.9)
qj		2	qj

Проанализируем теперь матричные элементы VCrk k , 0 между колебательными состояниями кристалла в (6.2), которые выражаются через матричные элементы S K ,

поскольку именно структурный фактор содержит операторы рождения и уничтожения фононов:

	Cr
		k k ,
n'	V	k k ,	0	n	n'	S K	n .
n'	V		0	n	n'	S K	n .

Для этого представим S K в виде суммы трех слагаемых, смысл которых ясен из выражений (6.7), (6.8), (6.9):


S K		S0 K S1 K S2 K ...							(6.10)

S2 K

k ' k g

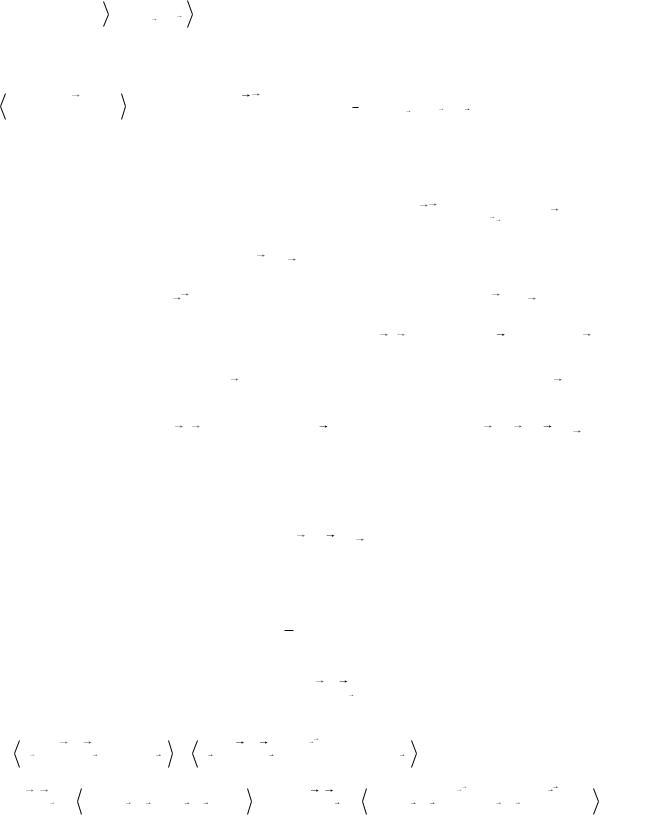
Если задать колебательное состояние кристалла как произведение состояний

осцилляторов

n qj

nqj (гармоническое приближение), то матричный элемент

между колебательными состояниями равен:

S0 K

exp iKl n ' , n K

n ' qj ,n

(6.11)

т.е. рассеяние благодаря первому слагаемому в правой части (6.9) и (6.10) оставляет колебательное состояние решетки неизменным (бесфононное рассеяние). Примечательная

особенность (6.11) заключается в том,			что сумма exp iKl N Kg , где			g вектор
				l
обратной решетки. Формально, при			K g каждое слагаемое суммы равно			единице,
поскольку согласно Разд.1		gl 2 m ,	где m - целое число. Если же		K ' g ,	сумма по
векторам решетки равна		нулю. Действительно, пусть K 'l 2 m l , где l					-
величины при суммировании по l			равномерно заполняют интервал 0 l 2 .
Следовательно, exp iK 'l exp i l 0 . Равенство					K k ' k g		по

	l	l

существу выражает закон сохранения квазиволнового вектора частицы при ее рассеянии на кристалле и известно как условие образования дифракционных максимумов Лауэ.

Действительно, как будет показано ниже, при амплитуды рассеяния на различных

узлах решетки интерферируют конструктивно и обеспечивают максимум интенсивности рассеяния.

Можно показать, что слагаемое в (6.10) также дает вклад в бесфононное

рассеяние. Действительно, матричный элемент K Uqj

в (6.9) можно расписать:

K Uqj aˆqje

к.с.

iql

nqj

K Uqj

nqj nqj

aˆqj aˆqje2iql

aˆqjaˆqje 2iql

KUqj 2

n ' n KUqj 2

nqj'

aˆqj aˆqj aˆqj aˆqj

nqj

nqj'

nqj

Здесь мы видим, что только первое слагаемое в правой части этого выражения дает вклад в бесфононное рассеяние по отношению к осциллятору qj типа.

K U

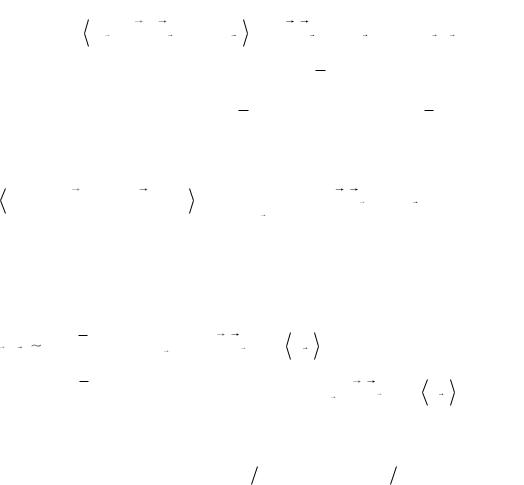
n ' qj,nqj

Аналогичным образом, только часть оператора S2 K

приводит к бесфононным процессам

рассеяния. Обозначая эту часть как

S 0 K

и объединив ее с

с учетом (6.7), (6.9),

(6.10) получим результирующую амплитуду бесфононного рассеяния:

S0 K S20 K

KUqj

,g 1

2nqj

1 n ' , n . (6.12)

Чтобы найти интенсивность процессов бесфононного рассеяния необходимо амплитуду

(6.2) с учетом (6.12) возвести в квадрат по модулю и результат усреднить по фононным состояниям всех осцилляторов:

Pk k '

Va K

,g qj 1 KUqj 2 2 nqj 1

V K

(6.13)

exp 2W ,

2 n

1 .

K ,g

Здесь использован замечательный предел

lim

N 1 n

N exp n

N .

Величину

exp 2W

называют фактором Дебая-Валлера;

она,

как

мы увидим ниже,

определяет зависимость интенсивности бесфононного рассеяния от температуры.

Рассеяние рентгеновских фотонов.

Условие Лауэ. Условие Брэгга-Вульфа.

Все вышеизложенное в равной мере справедливо как для частиц (электронов,

нейтронов), так и для электромагнитного излучения, рентгеновских и гамма фотонов.

Следует помнить, что электроны и рентгеновские фотоны в основном рассеиваются на электронной оболочке атомов, а гамма фотоны и нейтроны могут рассеиваться как на электронах, так и на ядрах. В последнем случае атомный потенциал Va следует заменить на ядерный потенциал VN . Далее будет весьма полезно конкретизировать полученные выше результаты для рентгеновского излучения. Именно бесфононное рассеяние рентгеновских лучей привело в свое время к возникновению рентгенодифракционного метода изучения структуры вещества. Отметим, прежде всего, возможности этого метода в определении

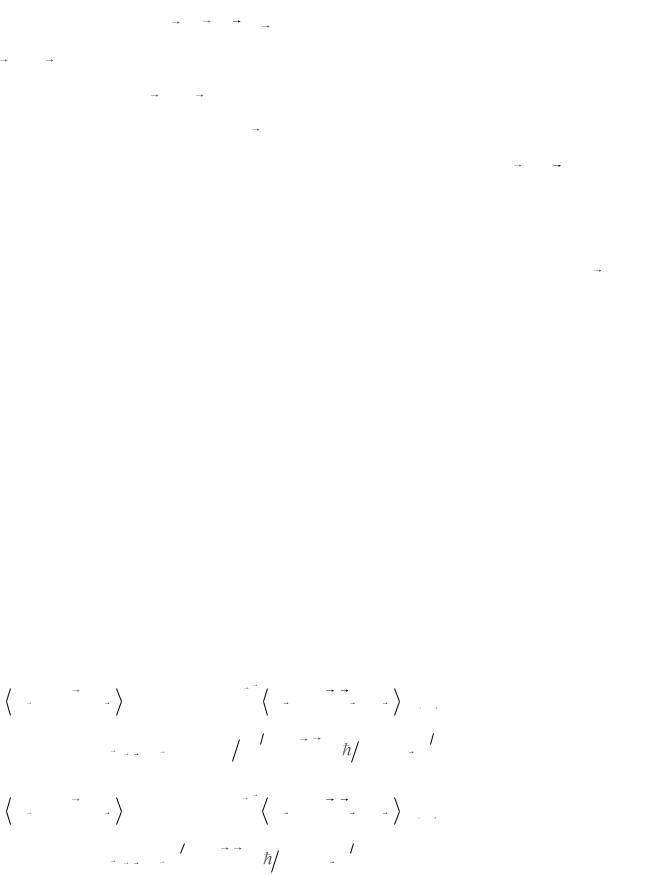
кристаллической структуры твердых тел – в рентгеноструктурном анализе.						Вернемся для
этого к условию образования дифракционных максимумов, условию Лауэ:
		K k ' k g ,		(6.14)
где k и	k ' - волновые вектора падающего и			рассеянного фотона. Согласно этому
соотношению измерение		k ' и k для возможных дифракционных максимумов позволяет
определить вектора обратной решетки			g и восстановить прямую решетку исследуемого
							k	k ),
кристалла.	Учитывая	бесфононный	(упругий)	характер рассеяния	(	k '	k	k ),

непосредственным построением (см. Рис.6.1) можно показать, что условие (6.14) может быть представлено как 2k sin g и далее 2d sin n (условие Брэгга-Вульфа, где 2 - угол рассеяния, d - расстояние между плоскостями прямой решетки, которым g

перпендикулярен (см. Разд.1)). Условие образования дифракционных максимумов по Брэггу-

Вульфу легко интерпретируется – разность хода лучей, рассеянных на разных плоскостях решетки должна быть кратна длине волны излучения (условие конструктивной интерференции). Реализация рентгеноструктурного метода сводится к экспериментальному определению набора векторов g для изучаемого кристалла и восстановлению по ним прямой решетки (см. Гл.1). Эта схема непосредственно применима к образцам в виде монокристалла (об особенностях получения информации о структуре поликристаллов см.

[1]).

Однофононное рассеяние

Второе слагаемое в (6.9) и (6.10) описывает однофононное рассеяние частиц или фотонов (число фононов любого из решеточных осцилляторов может измениться на единицу).

n 'qj

S1 K

nqj

q l

n 'qj

iKUqj

nqj

n 'qj ,nqj 1

(6.15)

K q ,g nqj 1 1

2 1 2 iK j

2mN qj 1 2 .

n 'qj

S1 K

nqj

q l

n 'qj

iKUqj

nqj

n 'qj ,nqj 1

(6.15’)

K q ,g nqj 1 2 iK j

2mN qj 1 2 .

Знак (+) в выражении (6.15) соответствует амплитуде рассеяния с одновременным рождением фонона, а знак (-) - амплитуде рассеяния с поглощением фонона. Вероятность последнего из этих двух процессов, вычисленная на основании (6.2), (6.15’), выглядит так:

nq nq 1		2	K	q,g KUqj	2	nqj k ' k qj . (6.16)
Pk k '	Va

Однофононное рассеяние - пример неупругого рассеяния, энергия и волновой вектор частицы (фотона) в процессе рассеяния меняются благодаря обмену энергией и квазиимпульсом с колебательной системой. Для процессов с поглощением фонона (см.

(6.16)) законы сохранения энергии и квазиимпульса следующие: k ' k qj и

k ' k q (полагая	g 0 ). Иными словами, изменение энергии рассеянной частицы равно
энергии поглощенного фонона (с		волновым вектором q ). Сопоставляя			значениям
q k ' k вдоль	определенного	направления	зоны	Бриллюэна	значения

k ' k , можно определить зависимость qj , т.е. закон дисперсии.

Успех в практической реализации этого метода зависит от типа используемого излучения. Прежде всего, волновой вектор частиц должен быть порядка или больше

размеров зоны Бриллюэна, поскольку q k ' k находится в зоне Бриллюэна. При этом

должна быть обеспечена возможность измерения энергии частиц с точностью порядка

E E k ' E k D 10 2 eV , где	D - максимальная энергия фононов в	модели
Дебая. Эти соображения свидетельствуют,	что эксперименты по определению	закона

дисперсии решеточных колебаний являются весьма затруднительными, если для этого

использовать	фотоны.	Волновому	вектору			k	a (рентгеновские	и гамма	фотоны)
соответствует энергия фотона E k
соответствует энергия фотона E k				c0k	104 eV . Обнаружить изменение этой энергии
на величину	меньше	10 2 eV	-	весьма сложная задача. С				другой	стороны,

сформулированные выше условия хорошо выполняются для нейтронного излучения.

Зависимость энергии нейтрона от волнового вектора EN k 2k 2		2M N	или
EN 2.1 k[ A 1] 2	10 3 eV . Т.е. энергия нейтрона с волновым вектором 1	A 1	того

же порядка, что и энергия фононов, что делает относительное изменение энергии нейтрона при рассеянии легко измеримым (см. более подробно[1], Т.2, гл. 24).

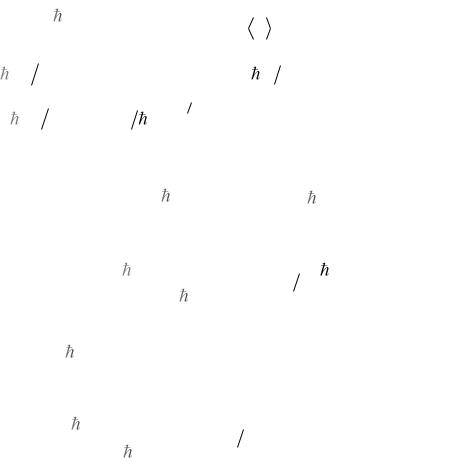
Существуют также процессы рассеяния с изменением числа фононов двух, трех и т.д.

осцилляторов. Для них легко могут быть записаны законы сохранения [1].

Фактор Дебая-Валлера.

Вернемся к фактору Дебая-Валлера, exp 2W , который определяет интенсивность дифракционных максимумов (см. (6.13)). Наша задача теперь заключается в проведении вычислений и получении зависимости этого параметра от температуры и от энергии рассеиваемых частиц (фотонов). Суммирование по решеточным осцилляторам в выражении для 2W (см. (6.13)) может быть заменено интегрированием по частотам от нуля до частоты Дебая D , используя функцию плотности решеточных колебаний в приближении Дебая,

(см. Разд. 5).

2W										K 2				D d 1gD 2 n 1
2W										K 2				D d 1gD 2 n 1
				2mN								0
				2mN											0
												зв			0
		K 2		4			2mN					3				D		d 2 exp											kT					1		1	1				(6.17)
		K 2		4			2mN					3						d 2 exp											kT					1			1				(6.17)
								D												0
3		K	2 2						3 m					kT					2		TD	T xdx				2 exp					x				1	1	1 .
Интеграл в (6.17) легко вычисляется для двух предельных случаев.
	T T						,						2W					6			2 K 2 kT 2							TD				6 2 K 2T						,			(6.18)
	T T						,						2W							2m kT				3														,			(6.18)
					D															2m kT				3					T				2mkTD2
																							D
T TD ,							2W						3 2 K 2 kT 2 T														2			3			2		2 K 2 1
																									D															.	(6.19)
																	3					3																		.	(6.19)
													4 m D										T												2m kTD

T T ,		2W				6			2k 2 kT 2										TD				3R T						,									(6.18’)
T T ,		2W														3													,									(6.18’)
D							2m kT									3			T kTD TD
														D

T TD ,					3					2k 2 kT 2 TD												2		3			2			R
		2W																													.								(6.19’)
		2W									3					3														kTD	.								(6.19’)
						4 m D													T											kTD

Здесь полезно привести взаимосвязь между 2W и среднеквадратичным смещением узла

решетки U 2	. Используя выражение (6.6) для U				l	, можно легко получить соотношение:
l					l
	2W	1	K 2 U 2 .			(6.20)
	2W		K 2 U 2 .			(6.20)
		3		l
		3

На основе (6.20) и (6.19) легко убедиться, что среднеквадратичное смещение Ul2 при

нулевой температуре имеет конечное значение, в противоположность классическим ожиданиям. Объяснение этому – нулевые колебания решетки.

Теперь рассмотрим зависимость фактора Дебая-Валлера от угла рассеяния. Она появляется при раскрытии K 2 k ' k 2 2k 2 1 cos 2 4k 2 sin2 , или

2W sin2 (см. рис. 6.1). Таким образом, фактор Дебая-Валлера определяет зависимость интенсивности дифракционных максимумов в спектре рассеяния от температуры. Ниже мы покажем, что фактор Дебая-Валлера определяет также вероятность бесфононных процессов

излучения и резонансного поглощения гамма квантов ядрами твердых тел.

Эффект Мессбауэра.

Согласно классической физике, при излучении гамма фотона покоящимся ядром последнему передается импульс k (в соответствии с законом сохранения импульса). В

результате этого вначале покоящееся ядро с массой M приобретает кинетическую энергию

R (энергию отдачи),

R	2k 2	2M E2 2Mc2 ,	(6.21)

а энергия излученного гамма фотона будет меньше энергии ядерного перехода E0 на R
(закон сохранения энергии), т.е. E	E0 R . Рассуждая аналогичным образом можно легко

придти к выводу, что резонансное поглощение гамма фотона покоящимся ядром возможно только при условии E E0 R (см. Рис.6.2б).

Приведенные выше соображения справедливы для свободных ядер, например, для вещества в газообразном состоянии, и не применимы к ядрам, находящимся в составе кристаллической решетки. Теперь мы не вправе применять закон сохранения импульса к

отдельному атому. Причина в том, что независимое поступательное движение выделенного атома в кристалле невозможно из-за его взаимодействия с остальными атомами решетки. В

кристалле, как мы выше убедились, движение атомов (ядер) имеет колебательный характер и, более того, колебания являются коллективными.

Поэтому при переходе ядра из состояния В с энергией возбуждения E0

в основное

состояние А

со спонтанным излучением гамма фотона естественно ожидать изменение

колебательного

состояния

кристалла

n n' .

Такой

переход

является

комбинированным, - одновременно имеют место переходы

в трех подсистемах: переход

В А

в ядре,

переход

между состояниями

поля гамма

излучения и

переход

n n'

между

колебательными состояниями кристалла. Такой переход

описывается амплитудой:

n n '

1k , n' , A

B, n ,0k

AB A

Hint k

(6.22)

где 0k

и 1k

- числа гамма

фотонов с волновым вектором k в начальном и конечном

состояниях, а

оператор Hint

k N

L bk к.с. ответственен

за переходы в трех

подсистемах:

оператор

рождения

гамма фотона,

L exp ik Ul

зависит от

операторов рождения (уничтожения)

нуклонов и отвечает за переход ядра

(6.22) запишем как:

n n '	A	ˆ	B

AB A		N

фононов, ˆ зависит от внутренних координат

В А . Таким образом, учитывая 1k				ˆ	0k	1,
				ˆ
				bk
n'	exp ik Ul	n .	(6.23)
n'	exp ik Ul	n .	(6.23)

Далее нас интересует роль последнего множителя в (6.23) - матричного элемента оператора

exp ik Ul	между колебательными состояниями кристалла. Роль подобных матричных
элементов	уже обсуждалась выше, при вычислениях вероятностей бесфононных и

фононных процессов рассеяния внешнего (например, рентгеновского) излучения на

кристалле. Теперь нас интересует вероятность бесфононного излучения гамма фотона ядром в

кристалле. Она может быть получена путем возведения в квадрат n exp ik Ul n по

модулю и усреднением полученного выражения по фононным состояниям (по аналогии с

(6.13)).

PB A	exp 2W ,	2W	qj	k Uqj 2	2 nqj	1 . (6.24)
			qj

Это выражение означает, что вероятность бесфононного излучения ядер в кристалле задается фактором Дебая-Валлера, уже известным нам из теории бесфононного рассеяния частиц на кристалле. Зависимость 2W от температуры определяется выражениями (6.18) и (6.19),

после замены в них вектора рассеяния на волновой вектор излучаемого гамма фотона

K k .

6 2k 2 kT 2

3R T

T T ,

(6.18’)

2m kT

T kTD TD

T TD ,

2k 2 kT 2 T 2

3 2

(6.19’)

kTD

4 m D

Энергия гамма кванта E

при бесфононном излучении ядра равна энергии ядерного

перехода E0 , поэтому спектральную линию с энергией E

в спектре гамма излучения

называют несмещенной линией. При бесфононном излучении фотона энергия отдачи равна нулю, поэтому такой радиационный переход принято также называть безотдачным.

Несмещенная линия имеет естественную ширину, определяемую временем жизни

возбужденного ядерного уровня В. Кроме несмещенной линии в спектре гамма излучения имеются и фононные линии. Энергия фотона, соответствующего фононной линии меньше

(больше) энергии ядерного перехода E0 на величину суммарной энергии поглощенных

(излученных) фононов. Однако суммарная вероятность фононных переходов может оказаться заметно меньше вероятности (интенсивности) несмещенной линии. К тому же следует учесть, что энергии фононных линий распределены в диапазоне спектра,

превышающем естественную ширину несмещенной линии на 3-4 порядка. Все эти факторы приводят к тому, что спектр спонтанного излучения ядра в кристалле представляет очень узкую несмещенную линию на фоне широкого спектра, состоящего из фононных линий –

фононного крыла. Анализ резонансного поглощения гамма фотонов ядрами в твердых телах,

процесса, в известном смысле обратного спонтанному излучению, показывает, что спектр поглощения опять содержит несмещенную линию (с естественной шириной) на фоне широкой полосы фононных линий поглощения и вероятность бесфононного возбуждения ядер определяется фактором Дебая-Валлера. С учетом сказанного, легко убедиться в возможности возбуждения ядер в кристалле (поглотителе), используя гамма излучение,

испущенное возбужденными ядрами того же сорта, находящимися в другом кристалле

1 / 21 2 > Следующая >>>

Соседние файлы в папке ФТТ_Садыков_2012

#
10.02.2015337.03 Кб20FTT_Sadykov_1.pdf
#
10.02.2015967.18 Кб23FTT_Sadykov_2.pdf
#
10.02.2015409.34 Кб20FTT_Sadykov_3.pdf
#
10.02.2015417.43 Кб20FTT_Sadykov_4.pdf
#
10.02.2015613.27 Кб19FTT_Sadykov_5.pdf
#
10.02.2015553.51 Кб19FTT_Sadykov_6.pdf
#
10.02.2015571.76 Кб18FTT_Sadykov_7.pdf
#
10.02.2015386.84 Кб21FTT_Sadykov_8.pdf
#
10.02.201590.01 Кб20FTT_vvedenie.rtf
#
10.02.2015277.6 Кб21r929c.pdf
#
10.02.201525.6 Кб19Литератур_Содерж.doc