Задачи

Обязательные задачи

5.1.Стержень, находящийся в плоскости xOy, на котором могут свобод-

но двигаться две материальные точки с массами m1 и m2, соединенные между собой пружиной, вращается вокруг вертикальной оси Oz с постоянной угловой скоростью ω. Написать уравнения связей системы, определить число ее степеней свободы и ввести обобщенные координаты.

[z1 = z2 = 0, x1 sin ωt − y1 cosωt = 0, x2 sin ωt − y2 cosωt = 0; n = 2]

5.2.Найти число степеней свободы n плоского трехзвенного механизма

ABCD, у которого точки A и D могут перемещаться только по оси Ox. Как изменится результат для неплоского механизма?

[n = 3]

5.3. Свободная материальная точка движется под действием силы F(r,v,t) = Fxex + Fyey + Fzez . Найти выражения для обобщенных сил,

если в качестве обобщенных координат выбираются: а) цилиндрические координаты, б) сферические координаты.

5.4.Для сферического маятника длины l и массы m, изображенного на рисунке, с использованием в качестве обобщенных координат сферических углов θ и ϕ найти обобщенные силы Qθ и Qϕ.

5.5.Однородный стержень ОА, вес которого Р, может вращаться вокруг перпендикулярной к нему горизонтальной оси Оz без трения. К

концу А стержня прикреплена пружина BА, точка B крепления которой находится на оси Оx и отстоит от точки О по вертикали вверх на расстоянии BО = ОА = a. Длина пружины в ненапряженном состоянии равна l0. Используя в качестве обобщенной координаты системы угол ϕ,

который стержень образует с вертикалью, получить выражение соответствующей ему обобщенной силы, полагая, что коэффициент жесткости пружины равен с.

5.6.Две частицы с массами m1 и m2, соединенные между собой жестким стержнем длины l, притягиваются к неподвижной частице массы m по закону всемирного тяготения. Пренебрегая массой стержня, найти обобщенные силы, предполагая, что движение происходит в одной плоскости и

рассматривая в качестве обобщенных координат расстояние r и углы ϕ и ψ.

5.7.Наклонная призма А веса Р движется под действием горизонтальной силы F по гладкой горизонтальной плоскости. Вдоль наклонной плоскости призмы, расположенной под углом

α к горизонту, скользит доска В веса Q. Предполагая, что коэффициент трения доски о наклонную плоскость равен f, выбрать обобщенные координаты системы и определить соответствующие им обобщенные силы.

5.8.Найти обобщенные силы для материальной системы, изображенной на рисунке. Веса грузов А, В и С, соответственно, равны Р1, Р2 и Р3. Грузы А и В переме-

щаются по гладкой горизонтальной поверхности. Стержни длины l невесомы и соединены с грузами А и В и между собой идеальными цилиндрическими шарнирами и вся система движется в одной вер-

тикальной плоскости. Жесткости пружин, действующих на грузы A

иB, равны соответственно с1 и с2.

5.9.Найти функцию Лагранжа плоского маятника длиной l и массы m2 , точка подвеса которого (с массой m1 в ней) может совершать движение по горизонтальной прямой.

уравнений Лагранжа.

5.11. Составить функцию Лагранжа двойного плоского маятника, изображенного на рисунке, состоящего из двух частиц с массами m1 и m2, которые подвешены на нитях длиной l1 и l2 соответственно.

5.12.Составить функцию Лагранжа системы двух точек с массами m1 и

m2, движущихся в плоскости xOy по прямым, образующим углы π/4 с горизонталью. Предполагать, что на точки действует сила тяжести и что они все время находятся на неизменном расстоянии, равном a, друг от друга.

5.13.Две частицы с массами m1 и m2, связанные пружиной жесткости с, могут двигаться без трения по сторонам прямого угла xOy, сторона Oy которого вертикальна. Длина пружины в ненапряженном состоянии равна l0. Составить уравнения Лагранжа системы.

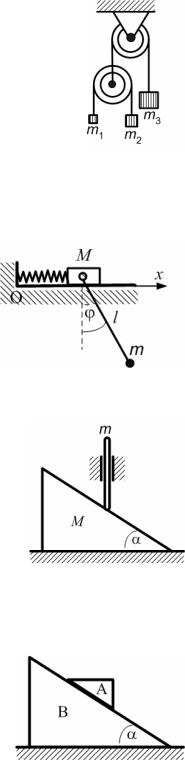
5.14.Через неподвижный блок, массой которого можно пренебречь, перекинута нить, на одном конце которой подвешена гиря массой m3, а на другом конце – невесомый блок. Через этот блок также перекинута нить, на концах которой подвешены гири массами m1 и m2. Предполагая, что трением при движении грузов мож-

но пренебречь, составить уравнения Лагранжа системы и определить ускорение, с которым будет двигаться гиря массой m3.

5.15.Тело массы M, соединенное с пружиной жесткости с, другой конец которой закреплен неподвижно, может двигаться по горизонтальной плоскости вдоль направления оси Ox. К телу прикреплен математический маятник массы m и длины l. Составить уравнения Лагранжа системы.

5.16.Стержень массы m может перемещаться без трения в вертикальной неподвижной муфте. Нижним концом он опирается на гипотенузу абсолютно гладкого клина массы M, который лежит на абсолютно гладкой горизонтальной

плоскости. Вследствие давления на него стержня клин движется горизонтально, а стержень при этом опускается. Используя уравнения Лагранжа, найти законы движения обоих тел.

5.17.Призма А веса Q скользит по гладкой боковой грани призмы В весом Р, образующей угол α с горизонтом. Определить движение обеих призм, предполагая, что трением меж-

ду призмой В и горизонтальной плоскостью можно пренебречь.