Экспериментальные исследования процессов рассеяния сводятся к измерению потока частиц до рассеяния и количества частиц, рассеиваю-

щихся под разными углами. Тем самым находят сечения рассеяния в лабо-

раторной системе координат. Теоретически эти величины можно найти, вычисляя dσ(θ) в ц-системе, а затем, определяя функции θ(θ1) и θ(θ2 ) из

диаграммы скоростей, основанной на решении (4.11). Дифференциальные

эффективные сечения рассеяния частиц первого и второго пучков в лабораторной системе можно далее получить как результат подстановки:

dσ1 = dσ(θ) θ=θ(θ1) , dσ2 = dσ(θ) θ=θ(θ2 ) .

Примеры решения задач

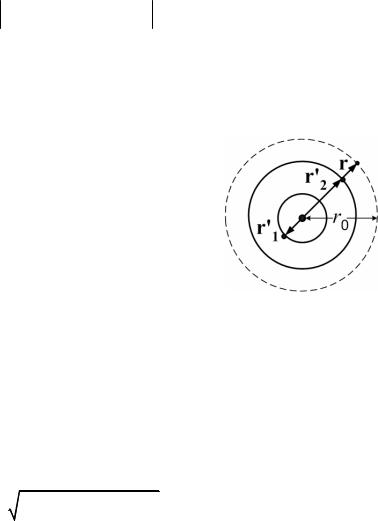
Задача 1. Две материальные точки массы m1 и m2 взаимодействуют по закону всемирного тяготения. Найти величины началь-

ных скоростей точек, при которых расстояние r0 меж-

ду ними во время движения не будет меняться.

Решение. В соответствии с (4.2) расстояние между точками есть модуль радиус-вектора μ-частицы, и по-

этому μ-частица будет двигаться по круговой траек-

тории. Также, согласно (4.6), будут двигаться и обе материальные точки в системе центра масс, причем они и μ-частица все время будут находиться на одной прямой, как показано на рисунке. Эксцентриситет круговой траектории μ-частицы, обладающей отрицательной полной энергией, в соот-

ветствии с результатами раздела 3 (см. формулу (3.6б)), можно записать в виде

где Е − есть полная энергия μ-частицы, М − величина ее момента количе-

ства движения, μ − приведенная масса и α − константа взаимодействия в

потенциале U = −α/ r, которая в данном случае гравитационного взаимодействия равна γm1m2. Из (4.18) для полной энергии Е находим

С другой стороны, полная энергия μ-частицы является интегралом движения и равна сумме кинетической и потенциальной энергии. В на-

Момент количества движения М μ-частицы также интеграл движения и в начальный момент времени для частицы, двигающейся со скоростью v0 по круговой траектории радиуса r0 , для него найдем

Приравнивая далее величины (4.19) и (4.20), с учетом (4.21) получаем уравнение

v04 −[2γ(m1 + m2 )/ r0 ]v02 + γ2 (m1 + m2 )2 / r02 = 0

для определения начальной скорости μ-частицы. Решая его, находим

v0 = γ(m1 + m2 ) / r0 .

Для начальных скоростей точек в движении, при котором расстояние r0 между ними во время движения не будет меняться в соответствии с

(4.10) получаем

Задача 2. Частица массы m1 до рассеяния покоится, а частица массы m2 в лабораторной системе координат движется со скоростью v. Определить величины и направления скоростей обеих частиц в лабораторной системе отсчета

после рассеяния как функции угла рассеяния θ в системе центра масс.

Решение. Поскольку скорость первой частицы до рассеяния v1− = 0, а ско-

рость второй частицы v−2 = v, то, согласно (4.9), μ-частица до рассеяния

двигается со скоростью v− = v−2 − v1− = v. Для скорости центра масс будем

иметь

Для скоростей первой и второй частиц до рассеяния в ц-системе найдем

После рассеяния частиц их скорости в ц-системе повернутся на угол θ и приобретут вид

С учетом (4.22) и в соответствии с (4.11) скорости обеих частиц после рас-

сеяния в лабораторной системе координат будут определяться выражениями

Умножая эти векторы скалярно сами на себя и извлекая из скалярных про-

изведений квадратные корни, получим величины скоростей обеих частиц после рассеяния

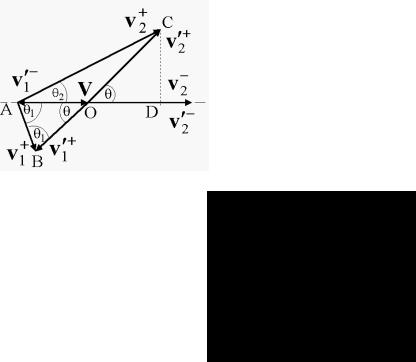
Для нахождения направлений скоростей обеих частиц после рассеяния воспользуемся диаграммой скоростей. Для ее построения (см. рису-

нок) выбираем некоторое направление, скажем горизонтальное, и вдоль

него от некоторой точки О в направлении направо откладываем вектор

скорости второй частицы до рассеяния в ц-сис- теме, в соответствии с (4.23) равный v′2− = m1v / m . Затем вдоль этой же прямой в противоположном направлении от той же точки О проводим вектор скорости первой частицы до рассеяния в ц-системе, в соответствии с

(4.23) равный v1′− = −m2v / m . Эти векторы всегда противоположно направлены, поскольку они выражаются через один и тот же вектор v скорости

μ-частицы c различными скалярными коэффициентами противоположны-

ми по знаку. В процессе рассеяния вектор v′2− поворачивается на угол рассеяния в ц-системе, не изменяясь по величине, и превращается в вектор v′2+ , поэтому изображаем его повернутым на угол θ, скажем против часо-

вой стрелки. Точно так же ведет себя и вектор v1′− , превращаясь в вектор v1′+ , оба вектора v′2+ и v1′+ , после рассеяния находятся на одной прямой. На рисунке мы изобразили векторы второй частицы большими по величине, допустив, что масса m1 > m2. Эта четверка векторов представляет собой диаграмму скоростей в ц-системе. Для того чтобы построить полную диаграмму скоростей, к ней необходимо присоединить вектор скорости центра масс. Чтобы иметь возможность получить векторы скоростей частиц в л-системе, вектор скорости центра масс следует провести так, чтобы он оканчивался в той точке, в которой начинаются все уже построенные че-

тыре вектора. Характер получаемой диаграммы будет зависеть от распо-

ложения вектора скорости центра масс. Если этот вектор не будет находиться в плоскости диаграммы ц-системы, то результирующая диаграмма будет иметь пространственный вид, если же он окажется в той же плоскости, то диаграмма будет плоской. В нашем случае вектор скорости центра масс, равный согласно (4.22) V = m2v / m, не только находится в плоскости

ц-диаграммы, так он еще и направлен по вектору v′2− , а по величине в точ-

ности совпадает с вектором v1′− . Диаграмма, таким образом, оказывается плоской, а вектор скорости центра масс мы должны провести так, чтобы он начинался в той же точке, в которой кончается вектор v1′− , а оканчивался в

точке О. Теперь для получения векторов скоростей в л-системе складываем вектор скорости центра масс с векторами скоростей частиц в ц-системе. В ча-

стности, добавляя к вектору V вектор v1′− , получаем вектор скорости первой частицы в л-системе v1− , который, как и дано в условии задачи, оказывается

равным нулю. Далее, складывая векторы V и v′2− , получаем вектор скорости второй частицы в л-системе v−2 , который направлен направо по горизон-

тальной прямой. Он начинается в точке А, а конец его совпадает с концом

торов V и v′2+ находим вектор v+2 . Угол θ1 между векторами v1+ и v1− по оп-

ределению является углом рассеяния первой частицы в лабораторной сис-

теме координат, но вектор v1− = 0, поэтому в данной ситуации угол θ1

приходится определять как угол между векторами v1+ и v−2 . Аналогичным образом, угол θ2 между векторами v+2 и v−2 определяет угол рассеяния

В любом случае, соотношения (4.26), (4.27), (4.28) или (4.29) полностью решают поставленную задачу, поскольку дают величины и направления векторов скоростей v1+ и v+2 как функции угла рассеяния θ в системе центра масс.

Задача 3. Частица с зарядом е и массой m, имеющая на бесконечности скорость v , налетает на такую же частицу, первоначально неподвижную, с прицельным расстоянием ρ. Найти скорости обеих частиц после рассеяния, предполагая, что частицы взаимодействуют по закону Кулона.

Решение. Общее решение для скоростей v1+ и v+2 можно получить сразу, если воспользоваться результатами решения предыдущей задачи. Достаточно лишь в выражения (4.26), (4.29) подставить условие равенства масс частиц: m1 = m2 = m. Имеем тогда

Из этих уравнений видим, что частицы после рассеяния двигаются под прямым углом друг к другу. Для нахождения связи между углом θ и прицельным расстоянием ρ вычислим интеграл, определяющий угол ϕ, подставив в (4.13) потенциал кулоновского взаимодействия U(r) = e2/r и учитывая, что приведенная масса μ для двух частиц одинаковой массы m равна m/2. Имеем

принять за начало отсчета угла ϕ и положить его равным нулю, то будем