
lecture239
.pdf
|
|
Зависимости |
|
|
|
||
. |
|
1 |
|
2 |
|
||
x=y |
|
y2 |
|
0 |
x2 1 |
||
C |
|
C |
C |
||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
x |
0 |
|
|
C |
|
|
|
|
0 |
2 |
|
|||
|
|
|
|
0 |
|
|
|
|
|
|
|
Собственное время |
|
1 |
|
||||||||||
|
2 |
|
0 |
|
|
|
t t |
|
|||||||||||
|
|
|
|||||||||||||||||
x |
|
|
0 x |
|
|
|
|
|
|
0 |
|
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
d2x |
|
|
|
d2x |
|
2 |
|
d2x |
||||||||
|
|
|
dt2 |
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 d 2 |
|||||||||||
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
d2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 d 2 0 x |
0 |
|
|
|
|
x x 0 |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||

Фазовый портрет
.
x=y
x
Итоги лекции:
Преобразование дифф. уравнения второго порядка в систему из двух дифф. уравнений первого порядка.
Фазовый портрет и для чего он нужен?
Определение особой точки типа центр?
Собственное время – абстракция от частоты колебаний.

Самостоятельная работа:
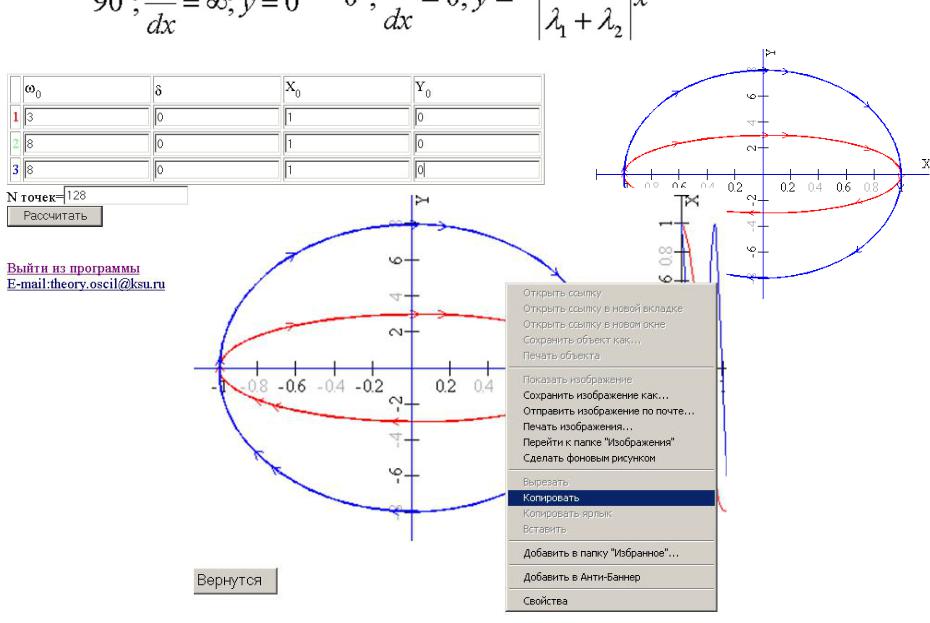
Используя web приложение «Расчет фазового портрета линейной системы с одной степенью свободы» построить фазовый портрет линейной консервативной системы.
Исследовать зависимость фазовых траекторий от начальных условий.
Исследовать зависимость фазовых траекторий от частоты колебаний.

Контроль самостоятельной работы:
http://www.ksu.ru/f6/b_files/work1!487.pdf
Контроль самостоятельной работы:
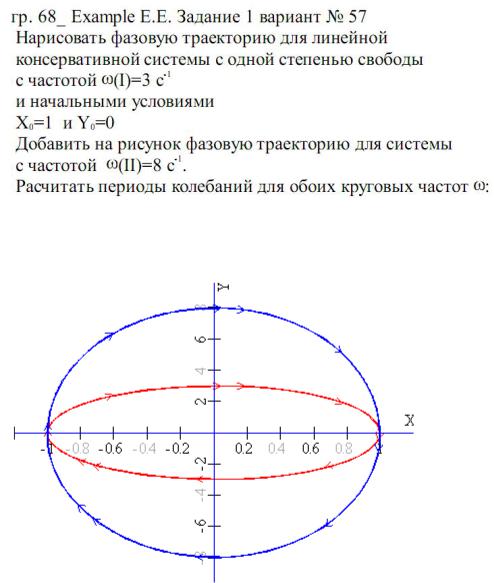
Контроль самостоятельной работы:
PDF->
Результаты Расчета ->
T(I)=2.1c T(II)=0.79c
WEB (CGI)->

Контроль самостоятельной работы:
