Однородное дифференциальное уравнение первого порядка

Так называют уравнение вида 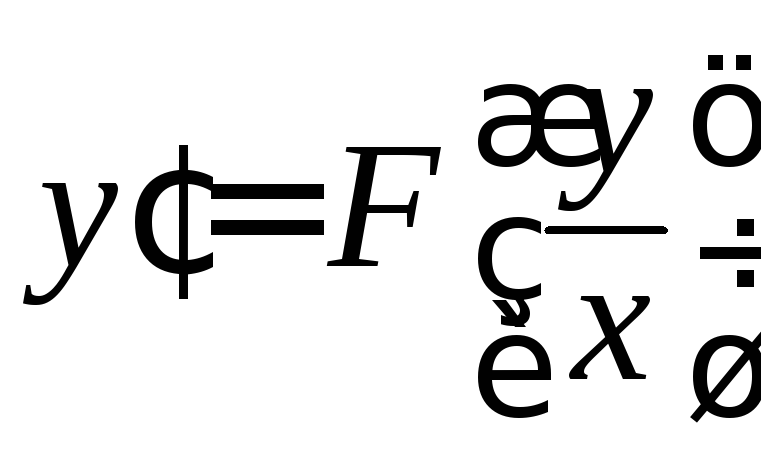. Для решения такого уравнения целесообразно ввести новую функцию. Тогдаи. Подставляя в исходное уравнение, получимили. Последнее уравнение – это уравнение с разделяющимися переменными. Решив его и найдя, мы найдем и.

П р и м е р. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс одинаково удалена от точки касания и от начала координат. Выбрать среди кривых ту, которая проходит через точку (2,1).

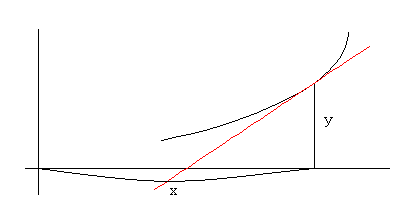
Решение. В соответствии с геометрическим условием . Упрощая, получим. Это однородное дифференциальное уравнение первого порядка. Вводя функцию, придем к уравнению с разделяющимися переменными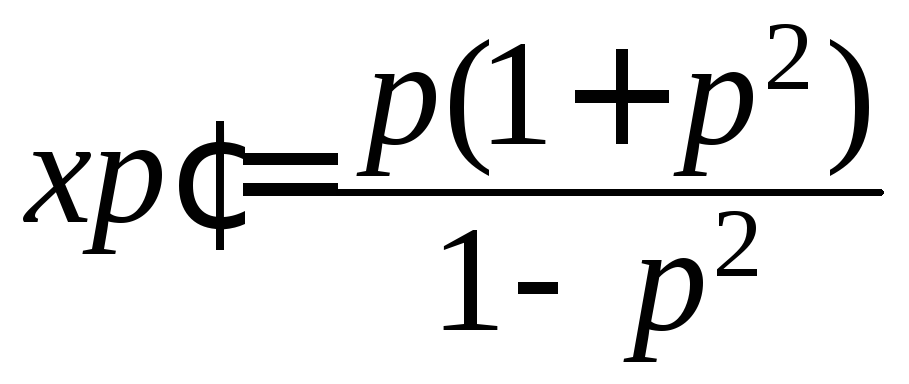. Разделив переменные, получим равенство дифференциалов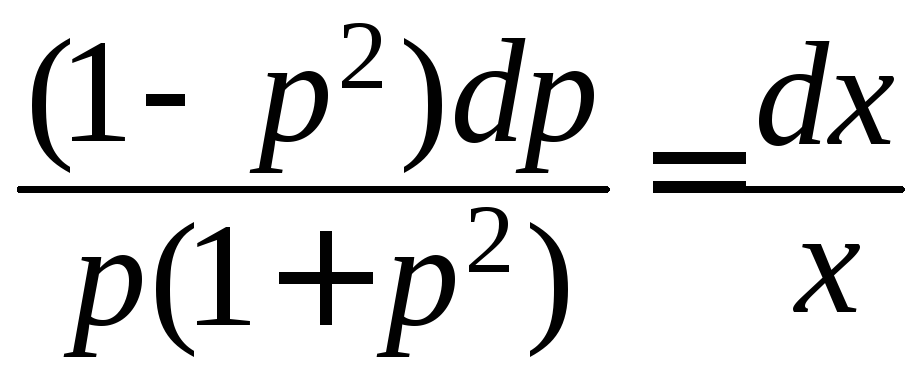. Левая дробь раскладывается на простейшие дроби следующим образом: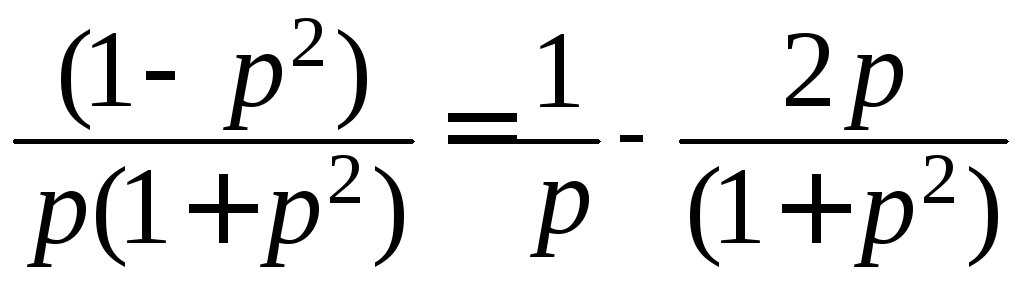. В результате после интегрирования имеем, и возвращаясь к старой функции по формуле, получим

. Семейство кривых мы построили. Теперь нужно выбрать ту кривую, которая проходит через точку (2,1). Подставляя координаты точки в уравнение, получим , то есть,. Таким образом, уравнение выбранной кривой:.

Пример анализа решений дифференциального уравнения с разделяющимися переменными

Это пример связан с применением дифференциальных уравнений с разделяющимися переменными в экологии.

Логистическая кривая.

Рассмотрим уравнение роста популяции за счет размножения. Пусть какая-то популяция, например, популяция рыб, запущенных в пруд, растет вследствие хороших условий из-за естественного прироста количества особей. Первое время, пока рыб немного, скорость прироста пропорциональна количеству рыб в водоеме. Если обозначить количество особей , то дифференциальным уравнением будет, и значит, решением будет экспоненциальная функция, где числоозначает начальное количество рыб, а положительный коэффициентотражает условия размножения рыб. Однако бесконечно количество особей увеличиваться не может вследствие ограниченности водоема, количества кислорода в нем и корма. При определенном количестве рыб начинаются болезни, кислородное голодание, и увеличивается смертность. Поэтому коэффициентявляется не числом, а функцией от, уменьшающейся при возрастании. Заменим дифференциальное уравнение роста популяции дифференциальным уравнением. Решим это уравнение и получим неявную зависимостьв видеили. Очевидно, что приимеем(красная прямая) вне зависимости от знака разности.

Если продифференцировать по переменной обе части соотношения

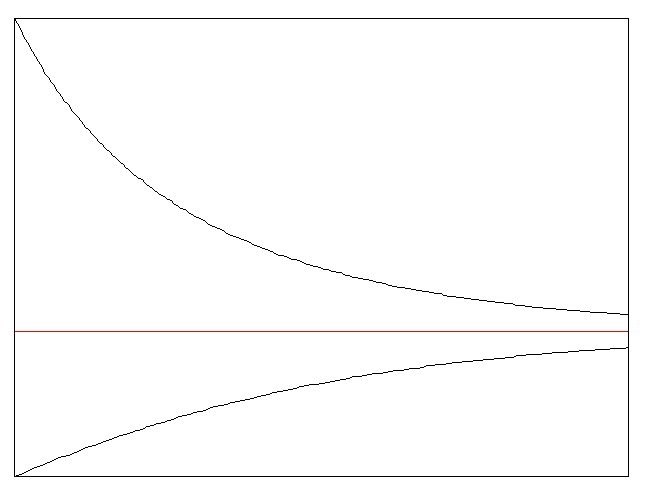
, получим: . Это значит, что если, то соответствующее решение (логистическая кривая) возрастает к значениюс ростом, а если, то логистическая кривая убывает к значениюс ростом.

Квоты отлова.

Продолжая тему исследования популяции рыб в водоеме, предположим, что во избежание вымирания лишних рыб следует отрегулировать регулярный отлов части рыбы. Предположим, что скорость отлова задана и равна . Тогда дифференциальное уравнение примет вид.

Решая это уравнение с разделяющимися переменными, придем к соотношению . Вид первообразной слева зависит от дискриминанта квадратного трехчлена в знаменателе.

Пусть . Тогда общее решение дифференциального уравнения имеет вид:, и вне зависимости от начального значения, связанного с выбором константы, с ростомзначениебудет уменьшаться, пока не примет значения 0. Таким образом, при квоте отловарыба в водоеме исчезнет независимо от того, сколько ее запустить вначале.

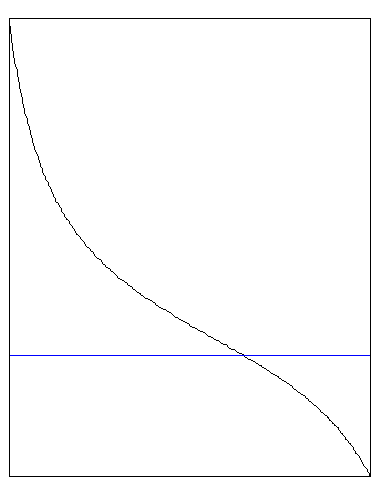
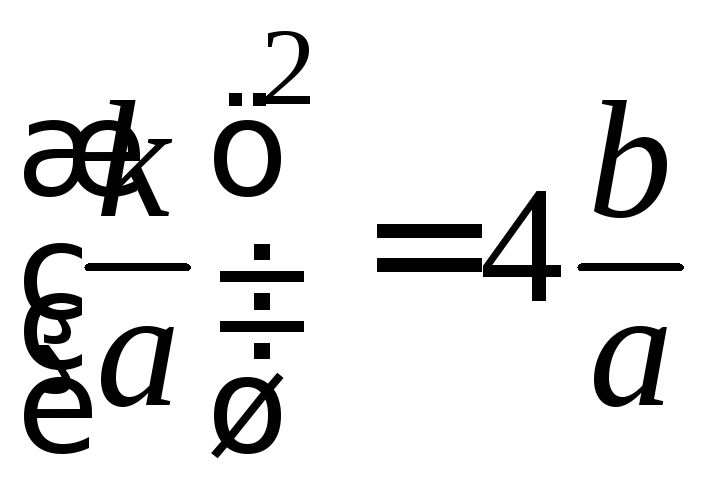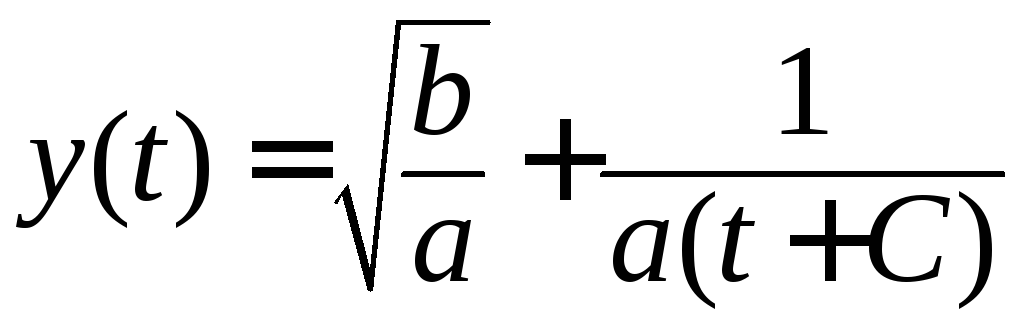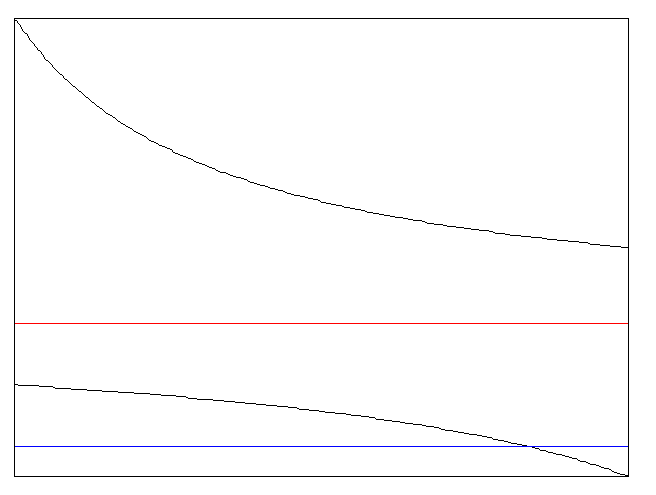
Пусть . Тогда решение имеет вид, и в случае начального значения, большегои связанного с выбором константы, количество рыбы будет уменьшаться, приближаясь к значению(красная прямая), всегда оставаясь больше этого значения. Если начальное значение меньше, рыба обречена на исчезновение.

Пусть 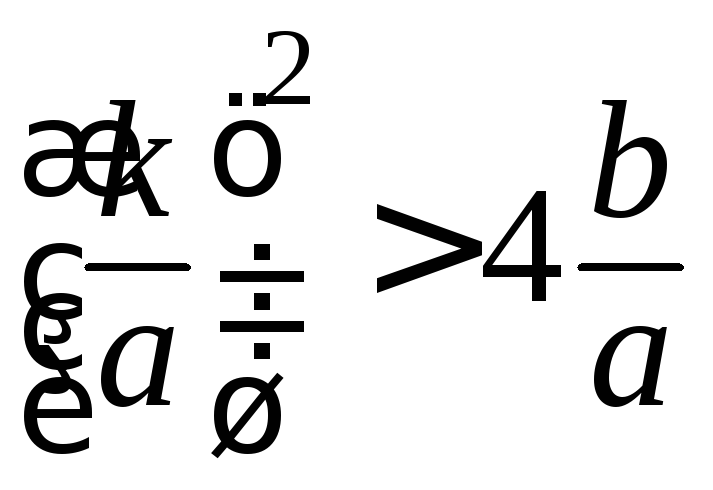. Тогда, где. Поэтому решение дифференциального уравнения можно записать в виде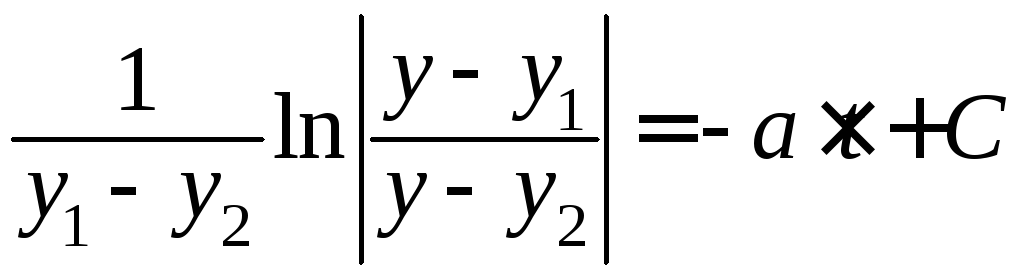. Очевидно, что приимеем. Возьмем производную поот обеих частей соотношения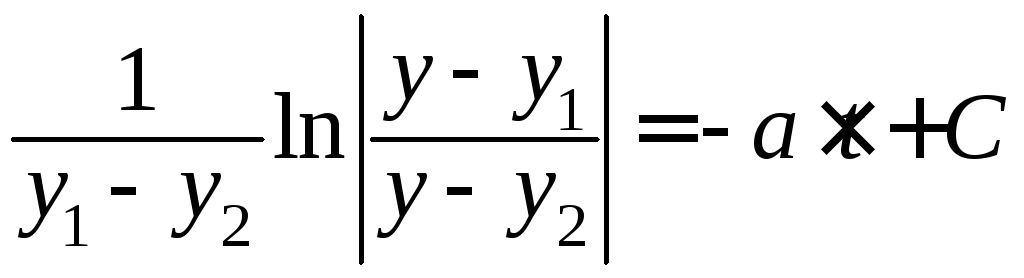и получим. Это значит, что кривая, представляющая решение, убывает прии при, а прикривая возрастает.

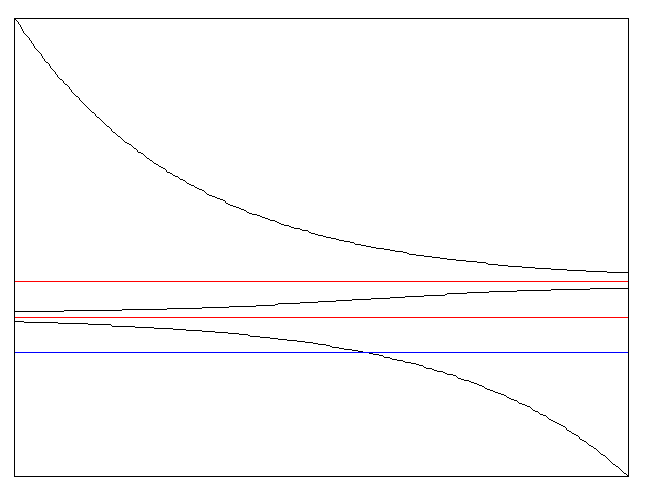
На соответствующем графике (в так называемой фазовой плоскости) прямые обозначены красным цветом. Прямаяобозначена голубым цветом.