6.109 А) ;

б) ;

в) .

6.110 А) ;

б) ;

в) .

6.111 А) ;

б) ;

в) .

6.112 Найти наибольший объем, который может иметь прямоугольный параллелепипед, если:

а) площадь его поверхности равна S;

б) сумма длин его ребер равна a;

в) длина его диагонали равна ;

г) он вписан в полусферу радиуса R..

6.113 Найти наименьшую площадь поверхности, которую может иметь прямоугольный параллелепипед, если его объем равен V.

6.114 Определить наибольшую вместимость цилиндрического ведра, площадь поверхность которого (без крышки) равна S.

6.115 Определить наибольшую вместимость конической воронки, площадь поверхности которой равна S.

6.116. Найти точку , для которой сумма квадратов расстояний от прямых,,наименьшая.

6.117 В плоскости с вершинами,,найти точкусумма квадратов расстояний от которой до вершин треугольника является наименьшей.

6.118 Цены двух видов товара иравны соответственноиден.ед. за 1ед. товара Найти при каких объёмахипродаж этих товаров прибыль будет максимальной, если функция издержек имеет следующий вид:

а) , ,;

б) , ,.

6.119 Найти величины спроса ина два вида товара при ценах на них соответственнои, если потребитель при бюджетестремится максимизировать функцию полезности, которая имеет вид:.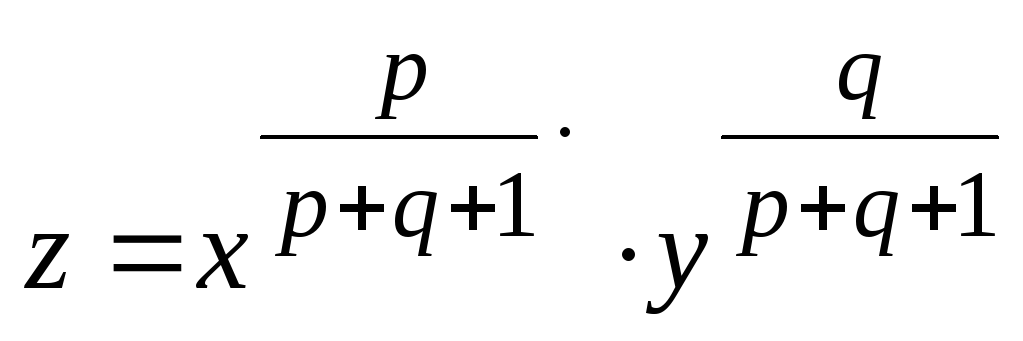

6.120 Цены двух видов ресурсов и, используемых для производства некоторой продукции равны соответственноиден.ед. в расчёте на 1ед. ресурса. Найти оптимальное распределение объёмов ресурсов, если производитель при бюджетестремится максимизировать функцию выпуска продукции, которая имеет вид.

Глава 7. Интегральное исчисление

ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ.

§1. Неопределённый интеграл.

Функция называетсяпервообразной для функции на промежутке, еслидля всех. Функцияможет иметь различные первообразные, но все они отличаются друг от друга только постоянными слагаемыми. Поэтому все первообразные длясодержатся в выражении, где- произвольная постоянная, которое и называетсянеопределённым интегралом от функции и обозначается. Таким образом, по определению.

Операция нахождения первообразной или неопределённого интеграла от функции называетсяинтегрированием этой функции. Функция для которой на промежуткесуществует первообразная или неопределённый интеграл называетсяинтегрируемой на этом промежутке. Первообразная и неопределённый интеграл на промежутке существуют у любой непрерывной на этом промежутке функции. Нахождение неопределённого интеграла состоит в таком преобразовании подынтегрального выражения, чтобы получить интегралы из таблицы основных интегралов (приложение №4).

Основные свойства неопределённого интеграла:

1. . 2..

3. ().

4. .

5. Если , то,.

Основными методами интегрирования являются: непосредственное интегрирование, интегрирование заменой переменной и по частям.

Непосредственным интегрированием (интегрированием методом разложения) функции называют отыскание неопределённого интегралас помощью тождественных преобразований подынтегральной функции, свойств3-4 неопределённого интеграла и таблицы основных интегралов.

148