В задачах 6.1-6.17 найти и изобразить графически область определения следующих функций:

6.1 . 6.2.

6.3 . 6.4.

6.5 . 6.6.

6.7 . 6.8.

6.9 . 6.10.

6.11 . 6.12.

6.13 . 6.14.

6.15 . 6.16. 6.17. 6.18.

6.19. Построить линии уровня следующих функций:

а) ; б); в); г).

Число называется пределом функциипри(или в точке), и пишут, если для любого числанайдётся числотакое, что при всех, удовлетворяющих условию, выполняется неравенство. Для функциипишут.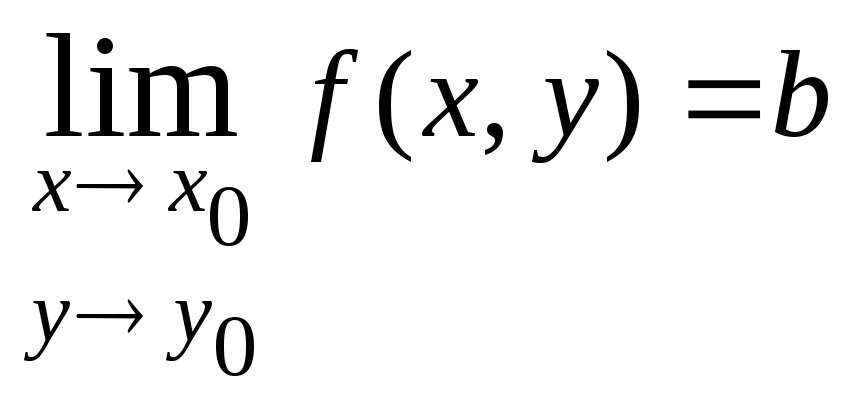

Вычисление предела функции нескольких переменных часто сводят к вычислению предела функции одной переменной с помощью замены переменных.

Функция называетсянепрерывной в точке , если. Функция непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Если в точке нарушено хотя бы одно из следующих условий:1) функция определена в точке ; 2) существует конечный предел ;3) , тоназываетсяточкой разрыва функции . Точки разрыва могут быть изолированными, образовывать линии разрыва, поверхности разрыва.

6.20 Найти следующие двойные пределы:

а) ; б) ;

в) ; г) .

6.21 Найти точки разрыва следующих функций:

а) ; б);

в) ; г).

§2. Частные производные

Частной производной (1-ого порядка) функции в точкепо переменнойназывается предел, если этот предел существует. Частную производную обозначаютили.

Частные производные вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что все аргументы функции, кроме аргумента , по которому берётся производная, постоянны.

Частными производными второго порядка функции называются частные производные от её частных производных первого порядка. При этом используются обозначения:

, ().

Производные () называютсясмешанными. Аналогично определяются и обозначаются частные производные порядка выше второго. Для функции частные производные обозначаются:

, ,,,,,… или,….

Если смешанные частные производные, подлежащие вычислению, непрерывны, то результат многократного дифференцирования функции по различным переменным не зависит от порядка дифференцирования.

В задачах 6.22-6.32 найти частные производные от следующих функций:

6.22 . 6.23.

6.24 . 6.25. 6.26. 6.27. 6.28. 6.29. 6.30. 6.31. 6.32.

В задачах 6.33-6.34 найти частные производные от следующих функций:

6.33 . 6.34.

6.35 Проверить равенство , если

а) ; б).

6.36 Проверить равенство , если

В задачах 6.37-6.40 найти указанные частные производные:

6.37 , если . 6.38, если.6.39,если.6.40,если .

§3 Дифференциал.

Полным приращением функции в точке, соответствующим приращениям аргументовназывается разность.

Функция называетсядифференцируемой в точке , если её полное приращение может быть представлено в виде, гдепри,- числа, не зависящие от_.

Полным дифференциалом функциив точкеназывается главная, линейная относительночастьполного приращенияфункции, равная, где.

Функция, обладающая в точкенепрерывными частными производными, всегда имеет в этой точке полный дифференциал. Для функциидифференцируемость в точке равносильна существованию в этой точке её полного дифференциала.

Форма записи первого дифференциала не изменится и в том случае, если переменные являются функциями новых, независимых переменных (свойство инвариантности формы первого дифференциала).

Дифференциалом 2-ого порядка функции называется дифференциал от её первого дифференциала и обозначается, т. е.. В общемдифференциалом порядка называется дифференциал от дифференциала-ого порядка и обозначается, т.е..

Если - независимая переменная, то для нахождения дифференциалафункциисправедлива символическая формула, формально раскрываемая по биномиальному закону. Например, для функциисправедливы формулы:,,

а для функции - формулы:,

.

Для функции -кратная дифференцируемость в точкеравносильна существованию в этой точке её полного дифференциала-ого порядка.

Если функция раз дифференцируема в точке, то в этой точке значение любой смешанной частной производной-ого порядка не зависит от порядка дифференцирования.

В задачах 6.41-6.46 найти дифференциалы первого и второго порядков от следующих функций: