
- •1.1.Основные методы вычисления неопределённого интеграла.
- •7.12 А); б); в).
- •7.51 А); б).
- •7.82 А); б); в).
- •7.91. 7.92. 7.93.
- •Основные свойства определённого интеграла:
- •7.198 А); б); в).
- •7.205 . 7.206. 7.207.
- •7.220 . 7.2217.222.
- •7.246 А) ;
- •7.247 А) ;
- •7.248 А) ;
- •7.249 А) ;
- •4.2 Приложения определенного интеграла к решению некоторых задач механики, физики и экономики.
7.82 А); б); в).
7.83 а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.84 а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.85 а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.86 а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.87 а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.88 а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.89
![]() ;
7.90
;
7.90![]() .
.
Интегралы вида
![]() ,
где
,
где![]() -рациональная
функция относительно аргументов
-рациональная
функция относительно аргументов![]() и
и![]() ,
приводятся к интегралам вида
,
приводятся к интегралам вида![]() ,
где
,
где![]() -рациональная
функция относительно аргумента
-рациональная
функция относительно аргумента![]() ,
с помощьюуниверсальной
тригонометрической подстановки
,
с помощьюуниверсальной
тригонометрической подстановки
![]() .
При этом используются формулы:
.
При этом используются формулы:![]() ,
,![]() ,
,![]() .
.
Применение универсальной подстановки, иногда приводит к громоздким вычислениям. В частных случаях используют подстановки:
1)
![]() ,
если
,
если![]() ,
при этом:
,
при этом:![]() ,
,![]() ;
;
2)
![]() ,
если
,
если![]() ,
при этом:
,
при этом:![]() ,
,![]() ;
;
3)
![]() ,
если
,
если![]() или
или![]() ,
при этом:
,
при этом:![]() ,
,![]() ,
,![]() ;
;
4)
![]() ,
если
,
если![]() ,
при этом
,
при этом![]() .
Здесь
.
Здесь![]() -
рациональная функция относительно
аргументов
-
рациональная функция относительно
аргументов![]() ,
,![]() .
.
Интегралы вида
![]() ,
где
,
где![]() ,
,![]() - целые неотрицательные числа, вычисляют,
преобразуя подынтегральную функцию с
помощью формул:
- целые неотрицательные числа, вычисляют,
преобразуя подынтегральную функцию с
помощью формул:![]() ,
,![]() .
.
Интегралы вида
![]() ,
,![]()
![]() ,
вычисляют, преобразуя подынтегральную
функцию по формулам:
,
вычисляют, преобразуя подынтегральную
функцию по формулам:
![]() ;
;
![]() ;
;
![]() .
.
В задачах 7.91-7.118 найти следующие интегралы от тригонометрических функций:
7.91. 7.92. 7.93.
7.94![]() .
7.95
.
7.95![]() .
7.96
.
7.96![]() .
.
7.97![]() .
7.98
.
7.98![]() .
7.99
.
7.99![]() .
.
7.100![]() .
7.101
.
7.101![]() .
7.102
.
7.102![]() .
.
7.103
![]() .
7.104
.
7.104![]() .
.
7.105![]() .
7.106
.
7.106![]() .
7.107
.
7.107![]() .
.
7.108![]() .
7.109
.
7.109![]() .
7.110
.
7.110![]() .
.
7.111![]() .
7.112
.
7.112![]() .
7.113
.
7.113![]() .
.
7.114![]() .
7.115
.
7.115![]() .
7.116
.
7.116![]() .
.
7.117![]() .
7.118
.
7.118![]() .
.
Интегрирование гиперболических функций аналогично интегрированию тригонометрических функций. При этом используются формулы:
![]() ;
;
![]() ;
;![]() ;
;![]() .
.
В задачах 7.119-7.130 найти следующие интегралы от гиперболических функций:
7.119![]() .
7.120
.
7.120![]() .
7.121
.
7.121![]() .
7.122
.
7.122![]() .
7.123
.
7.123![]() .
7.124
.
7.124![]() .
.
7.125![]() .
7.126
.
7.126![]() .
7.127
.
7.127![]() .
.
7.128
![]() .
7.129
.
7.129![]() .
7.130
.
7.130![]() .
.
Интегралы вида
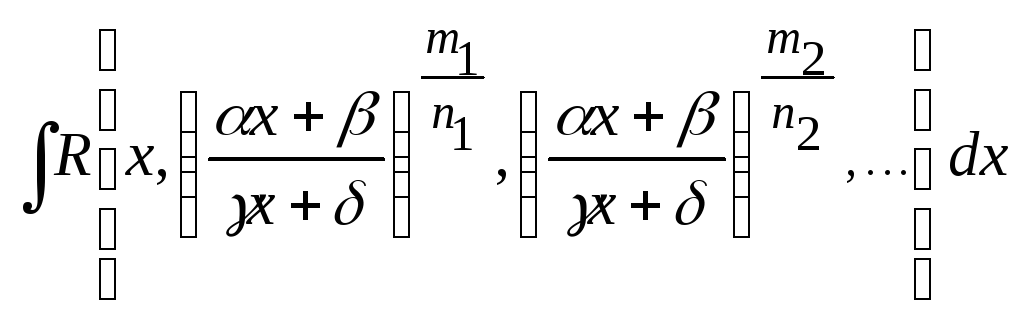 ,
где
,
где![]() -рациональная функция своих аргументов,
-рациональная функция своих аргументов,![]() -целые числа, вычисляются с помощью
подстановки
-целые числа, вычисляются с помощью
подстановки![]() ,
где
,
где![]() - наименьший общий знаменатель дробей
- наименьший общий знаменатель дробей![]() .
.
Вычисление
интегралов вида
![]() ,
где
,
где![]() -рациональная функция своих аргументов,
выделением полного квадрата в квадратном
трёхчлене
-рациональная функция своих аргументов,
выделением полного квадрата в квадратном
трёхчлене![]() и заменой
и заменой![]() ,
сводится к вычислению интегралов вида:
,
сводится к вычислению интегралов вида:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ,где
,где
![]() -
рациональная функция своих аргументов.
-
рациональная функция своих аргументов.
Последние интегралы, соответственно, с помощью тригонометрических или гиперболических подстановок:
1)![]() или
или
![]() ;
;
2)
![]() или
или
![]() ;
;
3)
![]() или
или
![]()
приводятся к
интегралам вида
![]() или
или![]() ,
где
,
где![]() -
рациональная функция своих аргументов
-
рациональная функция своих аргументов
В задачах 7.131-7.140 найти следующие интегралы от иррациональных функций:
7.131 а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.132 а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.133 а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.134а)![]() ;
б)
;
б)![]() ;в)
;в)![]()
7.135 а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7.136![]() .
7.137
.
7.137![]() .
7.138
.
7.138![]()
7.139
![]() .
7.140
.
7.140![]() .
.
1.3 Смешанные задачи на интегрирование.
В задачах 7.141-7.180 найти следующие интегралы:
7.141
![]() .
7.142
.
7.142![]() .
7.143
.
7.143![]() .
.
7.144![]() .
7.145
.
7.145![]() .
7.146
.
7.146![]() .
.
7.147![]() .
7.148
.
7.148![]() .
7.149
.
7.149![]() .
7.150
.
7.150![]() .
7.151
.
7.151![]() .
7.152
.
7.152![]() .
.
7.153![]() .
7.154
.
7.154![]() .
7.155
.
7.155![]() .
.
7.156![]() .
7.157
.
7.157![]() .
7.158
.
7.158![]()
7.159![]() .
7.160
.
7.160![]() .
7.161
.
7.161![]() .
7.162
.
7.162![]() .
7.163
.
7.163![]() 7.164
7.164![]() .
7.165
.
7.165![]() .
7.166
.
7.166![]() .
7.167
.
7.167![]() .
7.168
.
7.168![]() .
7.169
.
7.169![]() .
7.170
.
7.170![]() 7.171
7.171![]() .
7.172
.
7.172![]() 7.173
7.173![]() .
7.174
.
7.174![]() .
7.175
.
7.175![]() .
.
7.176![]() .
7.177
.
7.177![]() .
.
7.178![]() .
7.179
.
7.179![]() .
7.180
.
7.180![]() .
.
§2.Определённый интеграл и методы его вычисления.
К понятию
определённого интеграла можно прийти,
решая задачу о вычислении площади
криволинейной трапеции, т.е. фигуры,
заключённой между прямыми
![]() ,
,![]() ,
,![]() и кривой
и кривой![]() .
Число, равное площади криволинейной
трапеции, причём площадь той части,
которая лежит выше оси
.
Число, равное площади криволинейной
трапеции, причём площадь той части,
которая лежит выше оси![]() берётся со знаком «+», и ниже её – со
знаком «
берётся со знаком «+», и ниже её – со
знаком «![]() »
и называетсяопределённым
интегралом
от функции
»
и называетсяопределённым
интегралом
от функции
![]() на отрезке
на отрезке![]() .
Определённый интеграл обозначается
.
Определённый интеграл обозначается![]() ,
где числа
,
где числа![]() ,
,![]() называютсянижним
и верхним
пределами интегрирования.
называютсянижним
и верхним
пределами интегрирования.
Функция
![]() ,
для которой на отрезке
,
для которой на отрезке![]() существует определённый интеграл,
называетсяинтегрируемой
на этом отрезке. Достаточным
условием интегрируемости
функции
существует определённый интеграл,
называетсяинтегрируемой
на этом отрезке. Достаточным
условием интегрируемости
функции
![]() на отрезке
на отрезке![]() является её непрерывность на данном
отрезке.
является её непрерывность на данном
отрезке.
Если функция
![]() интегрируема на
интегрируема на![]() ,
то, по определению, полагают
,
то, по определению, полагают
![]() ,
,
![]() .
.
