8.140. 8.141. 8.142.

8.143. 8.144. 8.145. 8.146. 8.147. 8.148. 8.149. 8.150. 8.151. 8.152. 8.153. 8.154.

8.155. 8.156.8.157. 8.158. 8.159. 8.160.

Внутри общего интервала сходимости степенные ряды можно почленно складывать и вычитать, полученные при этом ряды имеют тот же интервал сходимости:

.

Внутри интервала сходимости степенной ряд можно почленно дифференцировать и интегрировать, полученные при этом ряды имеют тот же интервал сходимости:

1) ;

2) .

Степенной ряд называетсярядом Тейлора функции в точке. Приряд Тейлора называетсярядом Маклорена: .

Представление функции в виде, называется разложениемв ряд Тейлора. Равенство имеет место тогда и только тогда, когда остаток рядапридля всехиз некоторой окрестности точки, входящей в интервал сходимости ряда. Для оценки остатка ряда Тейлора часто пользуются формулой, где.

При разложении функций в степенные ряды, как правило, используют основные разложения элементарных функций в ряд Маклорена (Приложение 5). Иногда при разложении используют почленное дифференцирование или интегрирование. При разложении в степенные ряды рациональных дробей рекомендуется представлять их в виде суммы простейших дробей.

В задачах 8.161-8.178 используя основные разложения элементарных функций (Приложение 5), а также возможность почленного дифференцирования и интегрирования степенных рядов, разложить функции в ряд Маклорена и указать интервалы сходимости полученных рядов.

8.161 . 8.162. 8.163.

8.164 . 8.165. 8.166.

8.167 . 8.168. 8.169.

8.170 . 8.171. 8.172.

8.173 . 8.174. 8.175.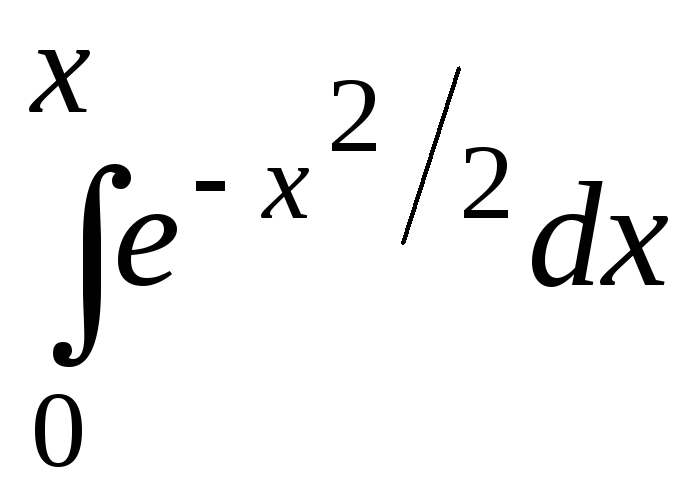

8.176 . 8.177. 8.178.

В задачах 8.179-8.186 вычислить указанные выражения с точностью .

8.179 . 8.180. 8.181. 8.182 .

8.183 . 8.184. 8.185. 8.186 .

8.187 Пользуясь тождеством вычислить числос точностью.

В задачах 8.188-8.193 вычислить следующие интегралы с точностью .

8.188 . 8.189. 8.190.

8.191 . 8.192. 8.193.

§4. Ряды Фурье. Интегралы Фурье.

Тригонометрическим рядом Фурье функции на отрезкеназывается функциональный ряд вида, где числаи, называемыекоэффициентами Фурье функции , вычисляются по формулам:

, ,.

Функция называетсякусочно-монотонной на отрезке , если этот отрезок можно разбить конечным числом точекна интервалытак, что на каждом из интервалов функция либо только возрастает, либо только убывает, либо постоянна.

Если функция на отрезкекусочно-монотонна и непрерывна, за исключением, быть может, конечного числа точек разрыва первого рода, то во всякой точке, в которойнепрерывна, функцию можно разложить в тригонометрический ряд Фурье. В точках разрывафункциии точкахсумма ряда Фурье определяется формуламии.

В частности, если: 1) функция -чётная, то в точках непрерывности функции имеет место разложение,где,;

2) функция -нечётная, то в точках непрерывности функции имеет место разложение, где,.

Если функция задана только в интервале, то её можно продолжить в интерваллибо как чётную, либо как нечётную, а затем разложить её в интервалев неполный ряд Фурье по синусам или по косинусам.

В задачах 8.194-8.202 разложить следующие функции в ряд Фурье в интервале :