
- •§2. Геометрическая вероятность.
- •§3. Условная вероятность. Формулы сложения и умножения вероятностей.
- •§4. Формула полной вероятности. Формула Байеса.
- •§5. Схема Бернулли.
- •5.1 Формула Бернулли. Наивероятнейшее число появлений события.
- •5.2 Приближённые формулы Пуассона и Муавра-Лапласа.
- •§6 Одномерные случайные величины.
- •6.1 Дискретные случайные величины: законы распределения и числовые характеристики.
- •6.2 Непрерывные случайные величины: законы распределения и числовые характеристики.
- •12.146 ,.
- •§7 Основные законы распределения одномерных случайных величин.
- •7.1 Биномиальное распределение .
- •7.2 Распределение Пуассона .
- •7.3 Геометрическое распределение .
- •7.4 Равномерное распределение .
- •7.5 Показательное распределение .
- •7.6 Нормальное распределение .
- •§8 Многомерные случайные величины.
- •8.1 Дискретные двумерные случайные величины.
- •12.211 ,,,.
- •12.212 ,,,.
- •12.213 ,,,.
- •12.214 ,,,.
- •8.2 Непрерывные двумерные случайные величины.
- •1); 2) .
- •§10 Закон больших чисел и центральная предельная теорема
- •1) (В центрированной форме);
- •2) (В нецентрированной форме).
12.211 ,,,.
|
|
Y | ||
|
X |
1 |
2 |
4 |
|
1 |
0.05 |
0.1 |
0.25 |
|
2 |
0.15 |
0.2 |
0.25 |
12.212 ,,,.
|
|
Y | ||
|
X |
0 |
2 |
3 |
|
1 |
0.12 |
0.18 |
0.3 |
|
5 |
0.08 |
0.12 |
0.2 |
12.213 ,,,.
|
|
Y | ||
|
X |
0 |
1 |
5 |
|
2 |
0.06 |
0.34 |
0.03 |
|
4 |
0.14 |
0.36 |
0.07 |
12.214 ,,,.
|
|
Y | ||
|
X |
0 |
2 |
3 |
|
1 |
0.06 |
0.09 |
0.15 |
|
4 |
0.08 |
0.12 |
0.2 |
|
6 |
0.06 |
0.09 |
0.15 |
12.215 Бросается одна игральная кость.
Требуется:а)составить закон
распределения двумерной случайной
величины![]() ,
где случайные величины
,
где случайные величины![]() и
и![]() определяются
следующим образом: если при подбрасывании
игральной кости выпадает чётное число
очков, то
определяются
следующим образом: если при подбрасывании
игральной кости выпадает чётное число
очков, то![]() , в противном случае
, в противном случае![]() и
и![]() ,
когда число очков кратно трём, в противном
случае
,
когда число очков кратно трём, в противном
случае![]() ;б) выяснить являются ли величины
;б) выяснить являются ли величины![]() ,
,![]() зависимыми и вычислить коэффициент
корреляции
зависимыми и вычислить коэффициент
корреляции![]() .
.
12.216 Бросаются две игральные кости.
Требуется:а)составить закон
распределения двумерной случайной
величины![]() ,
где случайные величины
,
где случайные величины![]() и
и![]() определяются
следующим образом: если сумма очков на
игральных костях чётная, то
определяются
следующим образом: если сумма очков на
игральных костях чётная, то![]() ,
в противном случае
,
в противном случае![]() и
и![]() ,
если произведение очков на игральных
костях – чётное число, в противном
случае
,
если произведение очков на игральных
костях – чётное число, в противном
случае![]() ;б) выяснить являются ли величины
;б) выяснить являются ли величины![]() ,
,![]() зависимыми и вычислить их ковариацию
зависимыми и вычислить их ковариацию![]() .
.
12.217 Число![]() выбирается
случайным образом из множества целых
чисел:
выбирается
случайным образом из множества целых
чисел:![]() .
Затем из того же множества выбирается
наудачу число
.
Затем из того же множества выбирается
наудачу число![]() ,
больше первого или равное ему. Составить
закон распределения двумерной случайной
величины
,
больше первого или равное ему. Составить
закон распределения двумерной случайной
величины![]() и найти
и найти![]() .
.
12.218 Пусть![]() и
и![]() -произвольные
случайные величины. Доказать, что:
-произвольные
случайные величины. Доказать, что:
а)![]() ,
,
б)
![]() ,где
,где![]() .
.
12.219 Случайные величины![]() и
и![]() имеют математические ожидания
имеют математические ожидания![]() ,
,![]() ,
дисперсии
,
дисперсии![]() ,
,![]() и ковариацию
и ковариацию![]() .
Найти математическое ожидание и дисперсию
случайной величины
.
Найти математическое ожидание и дисперсию
случайной величины![]() .
.
12.220 Найти математические ожидания![]() ,
,![]() ,
дисперсии
,
дисперсии![]() ,
,![]() и ковариацию
и ковариацию![]() случайных величин
случайных величин![]() и
и![]() ,
если
,
если![]() ,
,![]() ,
а случайные величины
,
а случайные величины![]() и
и![]() имеют следующие числовые характеристики:
имеют следующие числовые характеристики:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
8.2 Непрерывные двумерные случайные величины.
Случайный вектор
![]() называется(абсолютно)
непрерывным,
если его функция распределения
представляется в виде
называется(абсолютно)
непрерывным,
если его функция распределения
представляется в виде
![]() ,
,![]() ,
,![]() ,
где
,
где![]() -неотрицательная
и интегрируемая в бесконечных пределах
функция, называемаяфункцией
плотности вероятностей (совместной).
Функция распределения
-неотрицательная
и интегрируемая в бесконечных пределах
функция, называемаяфункцией
плотности вероятностей (совместной).
Функция распределения![]() непрерывного
случайного вектора
непрерывного
случайного вектора![]() является
непрерывной функцией на всей числовой
плоскости.
является
непрерывной функцией на всей числовой
плоскости.
Функция
![]() является плотностью вероятностей
некоторого непрерывного случайного
вектора
является плотностью вероятностей
некоторого непрерывного случайного
вектора![]() ,
тогда и только тогда, когда:
,
тогда и только тогда, когда:
1); 2) .
В точках
непрерывности функции
![]() :
:![]() .
.
Для непрерывного
случайного вектора
![]() с плотностью вероятностей
с плотностью вероятностей![]() вероятность любого события вида
вероятность любого события вида![]() ,
,![]() вычисляется по формуле:
вычисляется по формуле:![]() .
.
Частные плотности
вероятностей
компонент находятся интегрированием
совместной плотности:
![]() ,
,![]() .
.
Непрерывные
случайные
величины![]() и
и![]() независимы
тогда и только тогда, когда
независимы
тогда и только тогда, когда
![]() ,
,![]() .
В противном случае они зависимы.
.
В противном случае они зависимы.
Числовые
характеристики
![]() ,
,![]() вычисляют по формулам:
вычисляют по формулам:![]()
![]() ,
,![]()
![]()
Вероятность
события
![]() ,
где
,
где![]() -постоянная
величина, находится по формуле
-постоянная
величина, находится по формуле![]() ,
где интегрирование распространяется
на все значения переменных
,
где интегрирование распространяется
на все значения переменных![]() ,
,![]() для которых
для которых![]() .
.
В задачах 12.221-12.222 двумерная
непрерывная случайная величина![]() задана
совместной функцией распределения
задана
совместной функцией распределения![]() .
Требуется:а)найти функции
распределения составляющих случайных
величин
.
Требуется:а)найти функции
распределения составляющих случайных
величин![]() ,
,![]() и выяснить являются они зависимыми или
нет;б) найти совместную функцию
плотности вероятностей
и выяснить являются они зависимыми или
нет;б) найти совместную функцию
плотности вероятностей![]() ;в) вычислить вероятность
;в) вычислить вероятность![]() для указанной области
для указанной области![]() .
.
12.221
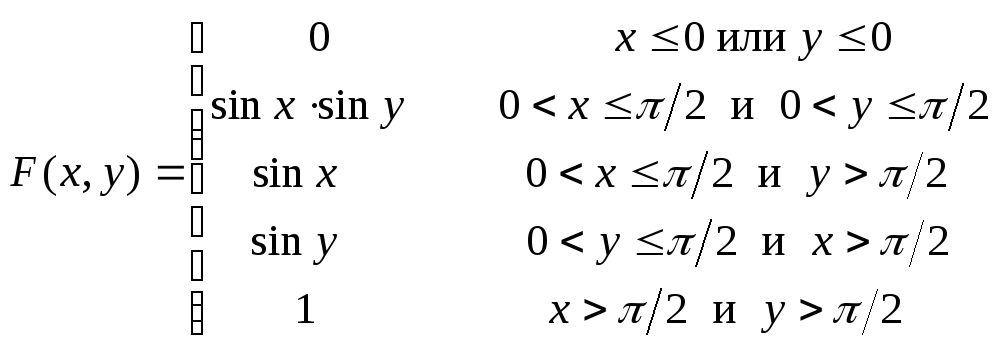
![]() - прямоугольник
- прямоугольник![]() ,
,![]() .
.
12.222
![]()
![]() - квадрат
- квадрат![]() ,
,![]() .
.
В задачах 12.223-12.224 двумерная
случайная величина![]() задана
совместной функцией плотности вероятностей
задана
совместной функцией плотности вероятностей![]() .Требуется:
.Требуется:
а)найти неизвестную постоянную![]() ;б)найти функции плотности вероятностей
составляющих случайных величин
;б)найти функции плотности вероятностей
составляющих случайных величин![]() ,
,![]() и выяснить являются они зависимыми или
нет;в) вычислить
и выяснить являются они зависимыми или
нет;в) вычислить![]() ,
,![]() ,
а также вероятность
,
а также вероятность![]() для указанного значения постоянной
для указанного значения постоянной![]() .
.
12.223
![]()
![]() .
.
12.224
![]()
![]() .
.
12.225 Двумерная случайная величина![]() равномерно распределена в указанной
области
равномерно распределена в указанной
области![]() .
Найти: совместную функцию плотности
вероятностей
.
Найти: совместную функцию плотности
вероятностей![]() ;
функции плотности вероятностей
составляющих случайных величин
;
функции плотности вероятностей
составляющих случайных величин![]() ,
,![]() и выяснить являются они зависимыми или
нет; центр рассеивания
и выяснить являются они зависимыми или
нет; центр рассеивания![]() ,
если:а)
,
если:а)![]() ;
;
б)![]() ;в)
;в)![]() .
.
§9 Функции случайных величин.
Пусть
![]() - случайная величина, заданная на
вероятностном пространстве
- случайная величина, заданная на
вероятностном пространстве![]() ,A,
,A,![]() )
и
)
и![]() - числовая функция, область определения
которой включает в себя множество
возможных значений
- числовая функция, область определения
которой включает в себя множество
возможных значений![]() . Случайную величину
. Случайную величину![]() ,
которая каждому
,
которая каждому![]() ставит в соответствие число
ставит в соответствие число![]() называютфункцией
от скалярной случайной величины
называютфункцией
от скалярной случайной величины
![]() и
пишут
и
пишут![]() .
.
Функция
![]() от дискретной случайной величины
от дискретной случайной величины![]() также является дискретной. Если
также является дискретной. Если![]() задана рядом распределения
задана рядом распределения![]() ,
,![]() ,
то рядом распределения случайной
величины
,
то рядом распределения случайной
величины![]() является ряд:
является ряд:![]() ,
,![]() ,
,![]() ,
где
,
где![]() -различные числа среди чисел
-различные числа среди чисел![]() ,
,![]() ( суммирование распространяется на все
значения индекса
( суммирование распространяется на все
значения индекса![]() для которых
для которых![]() ).
).
Функция
![]() от непрерывной случайной величины
от непрерывной случайной величины![]() может быть как непрерывной, так и
дискретной случайной величиной.
может быть как непрерывной, так и
дискретной случайной величиной.
Если
![]() задана плотностью вероятностей
задана плотностью вероятностей![]() и
и![]() является монотонной (возрастающей или
убывающей) дифференцируемой функцией,
то плотность вероятностей случайной
величины
является монотонной (возрастающей или
убывающей) дифференцируемой функцией,
то плотность вероятностей случайной
величины![]() определяется формулой:
определяется формулой: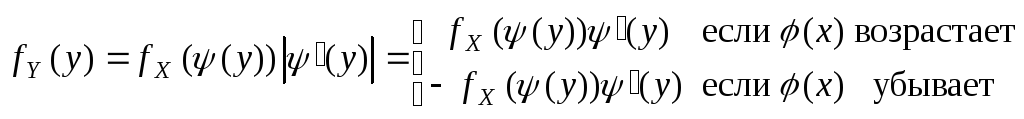 ,
где
,
где![]() - функция, обратная к функции
- функция, обратная к функции![]() .
Если
.
Если![]() является дифференцируемой кусочно-монотонной
(имеющей
является дифференцируемой кусочно-монотонной
(имеющей![]() интервалов монотонности) функцией, то
плотность вероятностей случайной
величины
интервалов монотонности) функцией, то
плотность вероятностей случайной
величины![]() определяется формулой
определяется формулой![]() ,
где
,
где![]() - функция, обратная к функции
- функция, обратная к функции![]() на
на![]() -ом
интервале её монотонности (возрастания
или убывания).
-ом
интервале её монотонности (возрастания
или убывания).
Для вычисления
числовых характеристик неслучайной
функции от случайной величины
![]() можно не знать закон распределения
зависящей от
можно не знать закон распределения
зависящей от![]() случайной величины
случайной величины![]() ,
а достаточно знать закон распределения
случайного аргумента
,
а достаточно знать закон распределения
случайного аргумента![]() .
Математическое ожидание и дисперсия
случайной величины
.
Математическое ожидание и дисперсия
случайной величины![]() ,
если они существуют, могут быть найдены
по формулам:
,
если они существуют, могут быть найдены
по формулам:
1)![]() ,
,![]() ,
если дискретная случайная величина
,
если дискретная случайная величина![]() задана рядом распределения
задана рядом распределения![]() ,
,![]() ,
где
,
где![]() ;2)
;2)
![]() ,
,![]() ,
если непрерывная случайная величина
,
если непрерывная случайная величина![]() задана плотностью вероятностей
задана плотностью вероятностей![]() .
.
Пусть
![]() - случайная вектор, заданный на
вероятностном пространстве
- случайная вектор, заданный на
вероятностном пространстве![]() ,A,
,A,![]() )
и
)
и![]() - числовая функция, область определения
которой включает в себя множество
возможных значений
- числовая функция, область определения
которой включает в себя множество
возможных значений![]() . Случайную величину
. Случайную величину![]() ,
которая каждому
,
которая каждому![]() ставит в соответствие число
ставит в соответствие число![]() называютфункцией
от случайного вектора
называютфункцией
от случайного вектора
![]() и пишут
и пишут![]() .
.
Функция
![]() от дискретного случайного вектора
от дискретного случайного вектора![]() также является дискретной. Если
также является дискретной. Если![]() задан таблицей распределения
задан таблицей распределения![]() ,
,![]() ,
,![]() ,
где
,
где![]() ,
то рядом распределения случайной
величины
,
то рядом распределения случайной
величины![]() является ряд:
является ряд:![]() ,
,![]() ,
где
,
где![]() - различные числа среди чисел
- различные числа среди чисел![]() ,
,![]() ,
,![]() ,
,![]() (суммирование распространяется на все
значения индексов
(суммирование распространяется на все
значения индексов![]() и
и![]() для которых
для которых![]() ).
).
Для вычисления
числовых характеристик неслучайной
функции от случайного вектора
![]() достаточно знать закон распределения
случайного аргумента
достаточно знать закон распределения
случайного аргумента![]() .
Математическое ожидание и дисперсия
случайной величины
.
Математическое ожидание и дисперсия
случайной величины![]() ,
если они существуют, могут быть найдены
по формулам:
,
если они существуют, могут быть найдены
по формулам:
1)
![]() ,
,![]() ,
если дискретный случайный вектор
,
если дискретный случайный вектор![]() задан таблицей распределения
задан таблицей распределения![]() ,
,![]() ,
,![]() ,
где
,
где![]() ;
;
2)
![]() ,
,![]() ,
если непрерывный случайный вектор
,
если непрерывный случайный вектор![]() задан совместной плотностью вероятностей
задан совместной плотностью вероятностей![]() .
.
12.226 Дискретная случайная величина![]() задана рядом распределения
задана рядом распределения![]()
![]() .
Найти распределение случайной величины
.
Найти распределение случайной величины![]() и вычислить
и вычислить![]() ,
если:
,
если:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
12.227 Распределение двумерной
дискретной случайной величины![]() задаётся таблицей распределения
вероятностей:
задаётся таблицей распределения
вероятностей:
|
|
Y | ||
|
X |
|
0 |
1 |
|
|
0.07 |
0.1 |
0.13 |
|
1 |
0.2 |
0.23 |
0.27 |
Найти ряд распределения вероятностей
случайной величины
![]() и вычислить
и вычислить![]() ,
если:
,
если:
а)![]() ;
б)
;
б)![]() .
.
12.228 Непрерывная случайная величина![]() ,
возможные значения которой заключены
в интервале
,
возможные значения которой заключены
в интервале![]() ,
задана функцией плотности вероятностей
,
задана функцией плотности вероятностей![]() .
Найти функцию плотности вероятностей
.
Найти функцию плотности вероятностей![]() случайной величины
случайной величины![]() ,
если:
,
если:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
12.229 Непрерывная случайная величина![]() равномерно распределена в интервале
равномерно распределена в интервале![]() .
Найти функцию плотности вероятностей
.
Найти функцию плотности вероятностей![]() случайной величины
случайной величины![]() ,
если:
,
если:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
12.230 Непрерывная случайная величина![]() имеет нормальный закон распределения
имеет нормальный закон распределения![]() ~
~![]() .
Доказать, что линейная функция
.
Доказать, что линейная функция![]() также имеет нормальный закон
распределения, причём
также имеет нормальный закон
распределения, причём![]() ,
,![]() .
.
12.231 Случайная величина![]() задана функцией плотности вероятностей
задана функцией плотности вероятностей![]() .
Найти математическое ожидание функции
.
Найти математическое ожидание функции![]() ,
если:
,
если:
а)
![]() б)
б)![]() .
.
12.232 Рассматривая диаметр круга![]() как случайную величину, распределённую
равномерно в интервале
как случайную величину, распределённую
равномерно в интервале![]() ,
найти математическое ожидание площади
круга
,
найти математическое ожидание площади
круга![]() .
.
12.233 Рассматривая ребро куба как
случайную величину![]() ,
распределённую равномерно в интервале
,
распределённую равномерно в интервале![]() ,
найти математическое ожидание объёма
куба
,
найти математическое ожидание объёма
куба![]() .
.
12.234 Непрерывная случайная величина![]() имеет показательное распределение с
параметром
имеет показательное распределение с
параметром![]() .
Найти математическое ожидание и дисперсию
случайной величины
.
Найти математическое ожидание и дисперсию
случайной величины![]() .
.
12.235 Случайные величины![]() и
и![]() независимы и распределены равномерно:
независимы и распределены равномерно:![]() - в интервале
- в интервале![]() ,
,![]() - в интервале
- в интервале![]() .
Найти
.
Найти![]() и
и![]() .
.
