2. Условный экстремум

2.1. Основные определения

В предыдущем параграфе рассматривалась задача на безусловный экстремум функции, то есть задача без ограничений на область изменения переменных. Однако во многих проблемах требуется отыскивать экстремум функции с условием, что аргумент может принимать значения только из некоторого множества .

Пусть – множество из, функцияопределена на. Задача минимизации функциина множественазываетсязадачей на условный минимум. При этом множество принято называтьдопустимой областью, точки –допустимыми, функцию –целевой функцией (критерием) задачи.

Введем некоторые определения.

Определение 1. Точка называетсяточкой условного глобального минимума функции на множестве, если для всехвыполняется неравенство.

Для краткости будем использовать термин «условный минимум функции», имея в виду точ-

ку минимума функции на . Обозначим

.

Определение 2. Точка называетсяточкой локального условного минимума функ-ции на множестве , если неравенствовыполняется для тех, которые принадлежат также некоторой окрестности точки .

Задача поиска и называется задачей условной минимизации функции .

Для анализа и решения этой задачи существенно то, как задано множество . В частности, далее рассмотрим два варианта:

1) допустимая область задана при помощи системы уравнений;

2) допустимая область задана при помощи системы неравенств.

2.2. Правило множителей Лагранжа

Рассмотрим так называемую классическую задачу на условный минимум или задачу с ограничениями в виде уравнений.

Пусть на заданы функции,.

Положим .

Таким образом, множество представляет собой некоторую поверхность в . Для условной оптимизации наиболее содержательны случаи, когда – собственное подмножество .

Теперь определим на вектор-функцию. Тогда, для краткости, запишем.

Введем следующую функцию:

,

где . Эта функцияпеременных называетсяфункцией Лагранжа. Переменные называютсямножителями Лагранжа.

Теорема 1. (Правило множителей Лагранжа) Пусть функции непрерывно дифференцируемы на , точка такова, что система векторовлинейно независима. Если– локальный минимум функции на множестве , то существует вектортакой, что

. (1)

Согласно определению функции Лагранжа условие (1) можно записать как систему равенств

.

Как использовать эту теорему для отыскания условных экстремумов? Составим систему

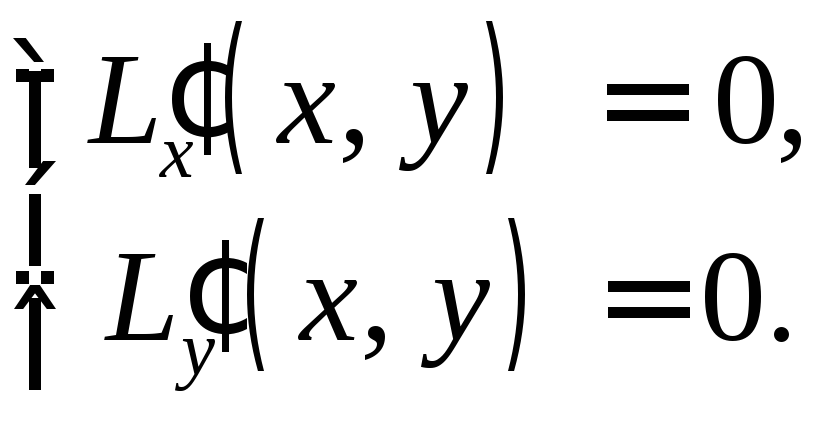(2)

Запишем систему (2) подробнее:

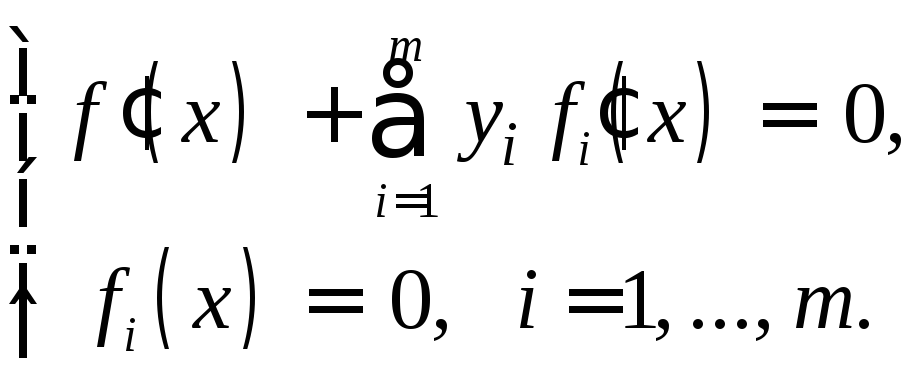
Она состоит из уравнений относительно переменных. Пусть вектор – некоторое ее решение. В этом случае вектор называется условно стационарной точкой функции . Таким образом, решая систему (2), мы можем найти все условно стационарные точки. Среди них содержатся все точки условного локального минимума.

Теорема 2. (Необходимое условие условного минимума второго порядка) Пусть выполнены все условия теоремы 1 и, кроме того, функция дважды дифференцируема в точке . Тогда для того, чтобы была локальным условным минимумом, необходимо, чтобы матрица была неотрицательно определена на подпространстве

.

Так как это условие является только необходимым, оно позволяет отсеять те из условно стационарных точек, которые не могут быть точками условного минимума.

Теорема 3. (Достаточное условие условного минимума второго порядка) Пусть выполнены все предположения теоремы 2. Тогда для того, чтобы условно стационарная точка была локальным условным минимумом, достаточно, чтобы матрица была положительно определена на подпространстве .

При помощи теорем 2 и 3 можно из условно стационарных точек отобрать точки условного локального минимума. Те же условно стационарные точки, которые не удовлетворяют этим теоремам, требуют дальнейшего исследования.