Изохорный процесс
При изохорном процессе выполняется условие dv = 0 или v = const. Из уравнения состояния идеального газа следует, что
.
Таким образом,
– уравнение процесса. (1)
На рис. 1 представлен график процесса в p-v и T-S координатах.
р Т v S q q
Рис. 1. График изохорного процесса
Работа изменения объёма
.
(2)
Количество теплоты, участвующей в процессе:
при постоянной
теплоемкости сv
=
const;
(3)
при
переменной теплоемкости сv
=
var.
(4)
Изменение внутренней энергии системы: согласно 1-му закону термодинамики
,
(5)
но так как dl = 0, то du = dq.
Тогда
.
(6)
Таким образом, в изохорном процессе вся теплота, подводимая к системе, затрачивается на изменение её внутренней энергии.
Поскольку внутренняя энергия идеального газа является функцией только его температуры, то и для любого термодинамического процесса идеального газа:
.
(7)
Изменение энтропии:
.
(8)
Изобарный процесс
При изобарном процессе выполняется условие dp = 0 или р = const. Из уравнения состояния идеального газа следует, что
.
Таким образом,
– уравнение процесса. (9)
На рис. 2 представлен график процесса в p-v и T-S координатах.
р q q Т v S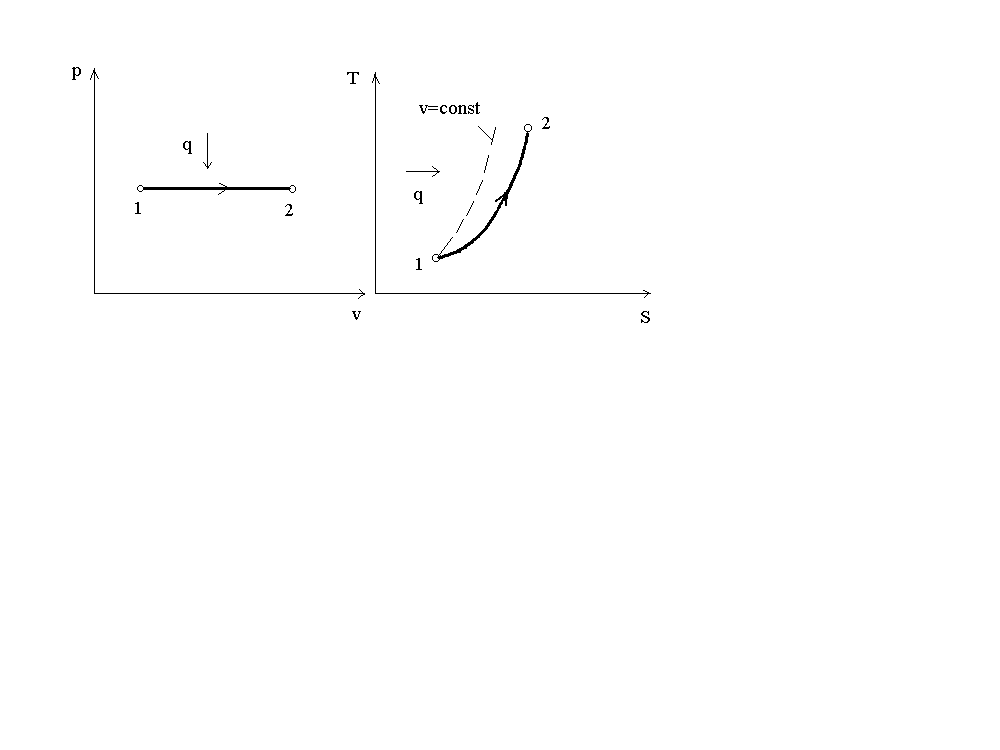
Рис. 2. График изобарного процесса
Работа изменения объёма
.
(10)
Количество теплоты, участвующей в процессе:
-
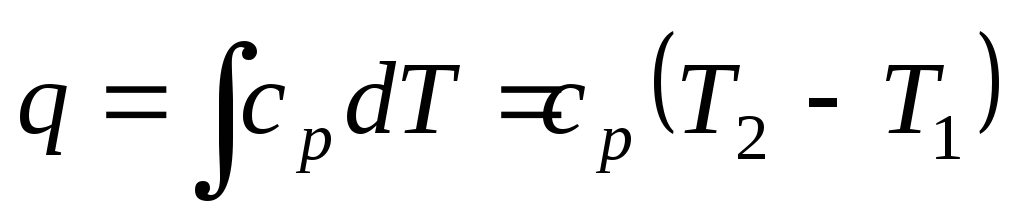–при постоянной
теплоемкости ср
= const;(11)
–при переменной
теплоемкости сv
= var.(12)
Изменение внутренней энергии системы:
.
(13)
Изменение энтропии:
.
(14)
Изотермический процесс
При изотермическом процессе выполняется условие dT =0 или Т = const. Из уравнения состояния идеального газа следует, что
.
Таким образом,
– уравнение процесса. (15)
На рис. 3 представлен график процесса в p-v и T-S координатах. В p-v координатах графиком процесса является равнобокая гипербола.
S q q Т v р
Рис. 3. График изотермического процесса
Работа изменения объёма:
.
(16)
Изменение внутренней энергии системы:
.
(17)
Количество теплоты, участвующей в процессе: согласно 1-му закону термодинамики
,
но так как du = 0, то dq = dl = рdv. (18)
Таким образом, в изотермическом процессе вся теплота, подводимая к системе, затрачивается на совершение работы изменения объёма.
Изменение энтропии:
.
(19)
Адиабатный процесс
Процесс, происходящий без теплообмена с окружающей средой, называется адиабатным. Таким образом, условие адиабатного процесса dq = 0.
Для того чтобы выполнялось данное условие, следует либо теплоизолировать газ, т.е. поместить его в адиабатную оболочку, либо провести процесс настолько быстро, чтобы изменение температуры газа, обусловленное его теплообменом с окружающей средой, было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа.
Уравнения 1-го закона термодинамики для адиабатного процесса имеют вид:
Поделив первое уравнение на второе, получают
или
,
где
– показатель адиабаты.
После интегрирования и потенцирования получают уравнение адиабаты:
или
.
(20)
Согласно молекулярно-кинетической теории показатель адиабаты для идеального газа не зависит от его температуры, а определяется только числом степеней молекулы газа. Для одноатомных газов k = 1,66; для 2-х атомных – k = 1,4; для 3-х и многоатомных – k = 1,33.
Поскольку k 1, то в координатах p-v линия адиабаты идет круче линии изотермы. На рис.4 представлен график адиабатного процесса в сравнении с графиком изотермического.
v р S Т
Рис. 4. График адиабатного процесса
При адиабатном расширении давление понижается быстрее, чем при изотермическом расширении, т.к. при этом происходит уменьшение температуры газа.
Параметры состояния в адиабатном процессе связаны следующими соотношениями
(21)
Изменение внутренней энергии системы:
.
(22)
Работа изменения объёма системы: согласно 1-му закону термодинамики
|
|
(23) |
.
Таким образом, в адиабатном процессе работа совершается за счет изменения внутренней энергии системы.
Изменение энтропии:
.
(24)
В связи с тем, что в адиабатном процессе энтропия системы остается постоянной, иное название этого процесса – изоэнтропный.