41
3.4 Дробно-линейное программирование
Пусть стоит задача максимизации дробно-линейной функции
Q( X )
при линейных ограничениях:
n
Aij X
j 1
n
C0 C j X j
j 1
n
D0 Dj X j
j 1
j Bi |
(i 1...m). |
(3.10) |
X j 0 |
( j 1...n). |
(3.11) |
|
Предположим, что знаменатель в (2.1) положителен при всех X, удовле- |
|||
творяющих (3.10)–(3.11). |
|
|
|
Если обозначить |
|
|
|
n |
X j 1 , |
|
|
D0 Dj |
R 0, |
(3.12) |
|
j 1 |
R |
|
|
Z j |
RX j , |
|
|
то задача сведется к линейной программе максимизации |
|||
|
n |
|
|
Q(Z, R) C0R C j Z j |
|
||
|
j 1 |
|
|
при условиях: |
|
|
|
|
n |
|
|
D0R Dj Z j |
1, |
|
|
|
j 1 |
|
|
n |
|
|
|
Bi R Aij Z j 0, |
(i 1...m), |
||
j 1 |
|
|
|
R 0, Z j 0, ( j 1...n). |
|
||
· · · · · · · · · · · · · · · · · · · · · · · |
Пример 3.4 |
· · · · · · · · · · · · · · · · · · · · · · · |
|
Рассмотрим в качестве примера задачу максимизации
3+ 2X1 + 4X2 5X3
5+ 3X1 X2
при условиях:
X1 X2 0,
5X1 3X2 10X3 15,
X1, X2, X3 0.
42
С учетом (3.12) получаем задачу максимизации
3R 2Z1 4Z2 5Z3
при условиях:
|
|
|
5R 3Z1 Z2 1, |
|
|
|
|
|
||
|
|
|
Z1 Z2 |
0, |
|
|
|
|
|
|
|
|
15R 5Z1 3Z2 10Z3 0, |
|
|
|
|
||||
|
|
|
R 0, |
Z1, Z2, Z3 0. |
|
|
|
|
||
|
|
Таблица 3.3 – Поиск решения |
|
|
|
|||||
C |
Базис |
План |
–3 |
2 |
4 |
–5 |
0 |
0 |
–M –M |
|
баз |
плана |
Z |
R |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
Z6 |
Z7 |
–M |
Z6 |
1 |
5 |
3 |
–1 |
0 |
0 |
0 |
1 |
0 |
–M |
Z7 |
0 |
0 |
1 |
–1 |
0 |
–1 |
0 |
0 |
1 |
0 |
Z5 |
0 |
–15 5 |
3 |
10 |
0 |
1 |
0 |
0 |
|
|
k |
–M |
–5M |
–3M 2M 5 M |
0 |
0 0 |
||||
C |
|
Базис |
План |
–3 |
2 |
4 |
–5 |
0 |
0 |
–M |
баз |
|
плана |
Z |
R |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
Z7 |
|
|
|
|
|
|
|
|
|
|
|
–3 |
|
R |
1/5 |
1 |
3/5 |
–1/5 |
0 |
0 |
0 |
0 |
–M |
|
Z7 |
0 |
0 |
1 |
–1 |
0 |
–1 |
0 |
1 |
0 |
|
Z5 |
3 |
0 |
14 |
0 |
10 |
0 |
1 |
0 |
|
k |
–3/5 |
0 |
–M |
M+ |
5 |
M |
0 |
0 |
|
C |
|
Базис |
План |
–3 |
2 |
4 |
–5 |
0 |
0 |
|
баз |
|
плана |
Z |
R |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
|
–3 |
|
R |
1/5 |
1 |
0 |
2/5 |
0 |
3/5 |
0 |
|
2 |
|
Z1 |
0 |
0 |
1 |
–1 |
0 |
–1 |
0 |
|
0 |
|
Z5 |
3 |
0 |
0 |
14 |
10 |
14 |
1 |
|
|
k |
–3/5 |
0 |
0 |
–7.2 |
5 |
–3.8 |
0 |
|
|
C |
|
Базис |
План |
–3 |
2 |
4 |
–5 |
0 |
0 |
|
баз |
|
плана |
Z |
R |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
|
–3 |
|
R |
4/35 |
1 |
0 |
0 |
–2/7 |
1/5 |
–1/35 |
|
2 |
|
Z1 |
3/14 |
0 |
1 |
0 |
5/7 |
0 |
1/14 |
|
4 |
|
Z2 |
3/14 |
0 |
0 |
1 |
5/7 |
1 |
1/14 |
|
|
k |
33/35 |
0 |
0 |
0 |
1/7 |
17/5 |
13/35 |
|
|
Из таблицы 3.3 имеем Z1 Z2 3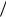
14, Z3 0, R 4
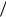35 и соответственно
Xopt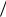 15
8,15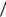
8,0 , max Q(X ) 33
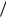35.
43
Заметим, что дробно-линейные программы в приложениях возникают достаточно часто; например, некорректная задача, преследующая взаимно противоположные цели типа максимизации прибыли при минимальных капиталовложениях, сводится к максимизации прибыли на единицу затрат.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Контрольные вопросы по главе 3
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
1.Почему в экономико-математических задачах может возникнуть нелинейность?
2.Какие существуют методы решения задач нелинейной оптимизации (нелинейного программирования)?
3.Что утверждает теорема Куна – Таккера?
4.В чем суть квадратичного программирования?
5.В чем суть дробно-линейного программирования?