113
8 Теория массового обслуживания
8.1 Понятие о задачах теории массового обслуживания
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Очереди возникают практически во всех системах массового
обслуживания (CМО) и теория массового обслуживания (теория очередей) занимается оценкой функционирования системы при заданных параметрах и поиском параметров, оптимальных по некоторым критериям.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Эта теория представляет особый раздел теории случайных процессов и использует, в основном, аппарат теории вероятностей. Первые публикации в этой области относятся к 20-м гг. XX в. и принадлежат датчанину А. Эрлангу, занимавшемуся исследованиями функционирования телефонных станций – типичных СМО, где случайны моменты вызова, факт занятости абонента или всех каналов, продолжительность разговора. В дальнейшем теория очередей нашла развитие в работах К. Пальма, Ф. Поллачека, А. Я. Хинчина, Б. В. Гнеденко, А. Кофмана, Р. Крюона, Т. Cаати и других советских и зарубежных математи-
ков [34].
В качестве основных элементов СМО следует выделить входной поток заявок, очередь на обслуживание, cистему (механизм) обслуживания и выходящий поток заявок. В роли заявок (требований, вызовов) могут выступать покупатели в магазине, телефонные вызовы, поезда при подходе к железнодорожному узлу, вагоны под разгрузкой, автомашины на станции техобслуживания, самолеты в ожидании разрешения на взлет и т. д. Роль обслуживающих приборов (каналов, линий) играют продавцы или кассиры в магазине, таможенники, пожарные машины, взлетно-посадочные полосы, экзаменаторы, ремонтные бригады.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
В зависимости от характеристик этих элементов СМО классифицируются следующим образом.
·· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
1.По характеру поступления заявок. Если интенсивность входного по-
тока (количество заявок в единицу времени) постоянна или является заданной функцией от времени, поток называют регулярным. Если па-
114
раметры потока независимы от конкретного момента времени, поток называют стационарным.
2.По количеству одновременно поступающих заявок. Поток с вероятно-
стью одновременного появления двух и более заявок, равной нулю, называется ординарным.
3.По связи между заявками. Если вероятность появления очередной заявки не зависит от количества предшествующих заявок, имеем дело с потоком без последействия.
4.По однородности заявок выделяют однородные и неоднородные потоки.
5.По ограниченности потока заявок различают замкнутые и разомкну-
тые системы (система с ограниченной клиентурой называется замкнутой). Так, универсальный магазин является разомкнутой системой, тогда как оптовый магазин с постоянными клиентами – замкнутая система.
6.По поведению в очереди системы делятся на системы с отказами (за-
явка покидает систему, если нет мест в очереди), c ограниченным ожиданием и с ожиданием без ограничения времени.
7.По дисциплине выбора на обслуживание. Здесь можно выделить си-
стемы с обслуживанием в порядке поступления, в случайном порядке, в порядке, обратном поступлению (последний пришел – первым обслужен), или с учетом приоритетов.
8.По числу каналов обслуживания системы разделяют на одно- и многоканальные.
9.По времени обслуживания выделяют системы с детерминированным
и случайным временем.
10.По количеству этапов обслуживания различают однофазные и многофазные системы.
8.2 Основы математического аппарата анализа простейших СМО
Рассмотрим стационарный поток однородных заявок без последействия. Пусть Pk τ – вероятность появления k заявок в интервале времени τ. Эта вероятность зависит только от τ и не зависит от начала отсчета времени, от поступления заявок в предыдущих временных интервалах. Пусть к тому же поток является ординарным, т. е. Pk dt при k 1 бесконечно мала в сравнении с ма-
115
лым интервалом dt. Если обозначить через λ число заявок в единицу времени (интенсивность потока), то можно показать, что для такого простейшего потока
P t (λ t)k |
e λ t . |
|
k |
k! |
|
|
|
|
Эта формула определяет распределение Пуассона. Для пуассоновского потока можно обнаружить, что промежутки времени T между поступлениями заявок распределены по экспоненциальному (показательному) закону:
P T t 1 e λ t
(вероятность, что промежуток времени не превышает t ).
|
Естественно, что входной поток может описываться не только пуассонов- |
||
ским, |
но |
и |
другими распределениями (Эрланга, гиперэкспоненциальным |
и т. п.). |
|
|
|
|
Аналогичная ситуация имеет место и для выходного потока. Чаще всего |
||
используется показательный закон распределения времени обслуживания: |
|||
|
|
|
P t 1 e μ t , |
где |
μ 1 tобс |
– интенсивность обслуживания (среднее число обслуживаний в |
|
единицу времени), |
|||
|
tобс |
– среднее время обслуживания одной заявки. |
|
|
Пусть S |
– множество состояний системы и P l,t τ i ,t – вероятность |
|
того, что система, находившаяся в момент t в состоянии i, в момент t τ окажется в состоянии l. Для марковской системы (она привлекает нас отсутствием последействия) можно записать уравнения Чепмена – Колмогорова:
P l,t τ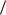
i ,t P j,t τ*
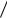i ,t P l,t τ
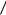j ,t τ* .
j S
Если под состояниями понимать число заявок, то эти уравнения можно записать в виде:
Pk t τ Pi t Pj τ .
i j k
Рассмотрим случай разомкнутой системы с простейшим входным потоком интенсивности λ и одним каналом обслуживания с интенсивностью μ.
Возьмем интервал времени t,t dt . |
В силу разомкнутости системы |
|
|
|
|
множество состояний системы
S S0 , S1, S2 ,..., Sk , Sk 1,... ,
где Sk – состояние, когда в системе находится k заявок.
116
Оценим вероятность перехода между состояниями с учетом того, что вероятность появления заявки в этом интервале времени равна λ dt и вероятность завершения обслуживания предшествующей заявки равна μ dt.
Очевидно, что вероятность перехода S0 S1 равна λ dt и вероятность пе-
рехода S1 S0 равна 1 λ dt. Если в системе присутствовали k 0 заявок (со-
стояние Sk ), то для перехода в состояние Sk 1 необходимо, чтобы заявка была обслужена и не поступило новой заявки; отсюда вероятность перехода
Sk |
Sk 1 равна μ dt 1 λ dt μ dt. Для перехода из состояния Sk в состояние |
Sk 1 необходимо, чтобы поступила новая заявка, но ни одна из ранее поступив- |
|
ших не была обслужена: |
вероятность перехода Sk Sk 1 |
равна λ dt |
1 μ dt |
|||
λ dt. Вероятность для |
системы остаться в |
том |
же |
состоянии |
составит |
|
1 λ μ dt. |
|
|
|
|
|
|
Тогда имеем |
|
|
|
|
|
|
P |
t dt 1 λ dt P t μ dt P |
t , |
|
|
||
0 |
|
0 |
1 |
|
|
|
Pk t dt λ dt Pk 1 t 1 λ dt μ dt Pk t μ dt Pk 1 t , k 0.
При dt 0 получаем дифференциальные уравнения состояний СМО:
|
|
|
d |
P |
t λ P |
t μ P |
t , |
|
||
|
|
|
dt |
|
||||||
|
|
|
0 |
0 |
|
1 |
|
|
||
d |
P |
t λ P |
|
t λ μ P |
t μ P |
t , k 0. |
||||
dt |
|
|||||||||
k |
|
k 1 |
|
|
k |
|
k 1 |
|
||
Это решение при заданных начальных условиях достаточно сложно (здесь можно использовать преобразование Лапласа или численное решение задачи Коши для системы обыкновенных дифференциальных уравнений большого порядка, но едва ли это посильно непрофессионалу) [34].
Ограничимся рассмотрением установившегося режима, признаком которого является существование предела
lim P |
t P , |
k 0,1,2,... |
t k |
k |
|
В этом случае мы получим бесконечную систему линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов:
λ P μ P , |
|
|
0 |
1 |
|
λ μ Pk λ Pk 1 μ Pk 1, |
k 1,2,... |
|
Обозначив
ρ λ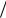
μ,
117
имеем
P ρ P , P |
ρ2P , P ρ3P , P |
ρ4P ,..., P |
ρk P ,..., |
|||||
1 |
0 2 |
0 |
3 |
0 4 |
0 |
|
k |
0 |
откуда с учетом |
|
|
|
|
|
|
|
|
|
|
P P P P ... P ... 1 |
|
|
||||
|
|
0 1 |
2 |
3 |
k |
|
|
|
получаем при ρ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
P0 1 ρ ρ2 ρ3 ... ρk ... P0 |
|
1. |
|||||
|
1 ρ |
|||||||
Тогда
P0 1 ρ
и
Pk ρk P0 для k 1,2,...
Обратите внимание на требование ρ 1. Если это требование нарушено, то ни о каком установившемся режиме не может быть речи: очередь растет неограниченно (средняя продолжительность обслуживания больше среднего интервала времени между заявками).
Теперь обратимся к аналогичной замкнутой системе с числом заявок, не превышающим n. Здесь система уравнений приведется к конечной системе:
d |
P |
t λ P |
t μ P t |
, |
|
|
|
|
dt |
|
|
|
|||||
0 |
0 |
1 |
|
|
|
|
||
d |
P |
t λ P |
t λ μ P |
t μ P |
t , |
k 1,2,..., n 1, |
||
dt |
||||||||
k |
k 1 |
|
k |
k 1 |
|
|
||
d |
P |
t μ P |
t λ P |
t , |
|
|
|
|
|
|
|
|
|||||
dt |
n |
n |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
которая для установившегося режима дает конечную систему линейных алгебраических уравнений
λ P μ P , |
|
|
0 |
1 |
|
λ μ Pk λ Pk 1 μ Pk 1, |
k 1,2,...,n 1, |
|
λ Pn 1 μ Pn.
Решение этой системы
P ρ P , P |
ρ2 P |
2, P ρ3 |
P |
2 3 , P |
ρ4 P |
2 3 4 ,..., P |
ρn P n! |
||
1 |
0 2 |
0 |
3 |
0 |
4 |
|
0 |
n |
0 |
дает |
|
|
|
|
|
|
|
|
|
|
|
|
|
P0 |
1 n |
ρ |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
k! |
|
|
|
и