105
Иногда в минимизируемую функцию включаются доходы, полученные от продажи остатков запаса в конце каждого периода. В некоторых случаях ставится задача максимизации доходов.
Ограничения в задачах управления запасами могут быть различного характера. Известны следующие виды ограничений:
по максимальному объему (весу, стоимости) запасов;
по средней стоимости;
по числу поставок в заданном интервале времени;
по максимальному объему (весу, стоимости) поставки или кратности этого объема некоторой минимальной величине (целое число стандартных «упаковок» – вагонов, бочек, коробок);
по доле требований, удовлетворяемых из наличного запаса (без до-
полнительных задержек).
Необходимо отметить, что область применения теории управления запасами отнюдь не ограничивается складскими операциями. Под запасами можно подразумевать: наличие товара; рабочую силу, планируемую для выполнения конкретного задания; объем информации в базе данных; численность персонала данной квалификации и т. д. Таким образом, при переосмысливании элементов модели методами теории управления запасами может быть решен широкий круг задач оптимального планирования.
7.3Детерминированные модели
Вэтом параграфе обсуждаются пять моделей. Большинство из них однопродуктовые, и только в одной из них учитывается влияние нескольких «конкурирующих» видов продукции. Основное различие между моделями определяется допущением о характере спроса (статический или динамический). Важным фактором с точки зрения формулировки и решения задачи является также вид функции затрат. Используются различные методы решения. Эти примеры наглядно показывают, что при решении задач управления запасами следует применять различные методы оптимизации [12].
7.3.1 Модель Уилсона
Рассмотрение моделей управления запасами начнем с простейшего слу-
чая.
106
Модель Уилсона, в определенном смысле классическая, основана на выборе такого фиксированного размера заказываемой партии, который минимизирует расходы на оформление заказа, доставку и хранение товара.
Экономическая партия товара вычисляется при следующих упрощениях реальной ситуации:
уровень запасов убывает с постоянной интенсивностью, и в тот момент, когда все запасы товара исчерпаны, подается заказ на поставку новой партии;
выполнение заказа осуществляется мгновенно, т. е. время доставки равно нулю и уровень запасов восстанавливается до значения, равного q;
накладные расходы, связанные с размещением заказа и поставкой товара, не зависят от объема партии и равны постоянной величине;
ежедневная стоимость хранения единицы товара равна постоянной
величине.
Данная политика, проводимая складом, характерна для тех случаев, когда интенсивность потребления запасов близка к постоянной величине, а поставки производятся регулярно.
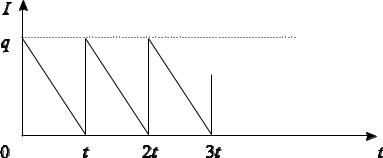
Простейшая модель оптимальной партии поставки строится при следующих предложениях: спрос ν в единицу времени является постоянным; заказанная партия доставляется одновременно; дефицит недопустим; затраты K на организацию поставки постоянны и не зависят от величины q партии; издержки содержания единицы продукции в течение единицы времени составляют s. На рисунке 7.3 показана динамика изменения уровня I запасов.
Рис. 7.3 – Динамика изменения уровня запасов
107
Уровень снижается равномерно от q до 0, после чего подается заказ на доставку новой партии величиной q. Заказ выполняется мгновенно и уровень запаса восстанавливается до величины q.
Интервал времени длиной t между поставками называется циклом. Издержки в течение цикла Lц состоят из стоимости доставки заказа K и
затрат на содержание запаса ν которые пропорциональны средней величине запаса I q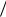
2 и длине цикла t q
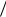ν,
Lц K s q2 qν .
Разделив это выражение на длину цикла t q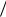
ν , получим издержки в единицу времени L :
L K qν s q2 .
Оптимальный размер партии определяется из уравнения:
dLdq Kq2ν 2s 0 (необходимый признак экстремума).
Отсюда находим оптимальный размер q* партии:
q* 
2Ks ν .
Так как d 2L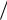
dq2 0 (достаточный признак экстремума), то для всех q 0 это выражение является минимумом функции затрат. Это уравнение известно под многими названиями. Его называют формулой наиболее экономной величи-
ны заказа, формулой Уилсона, формулой квадратного корня.
Чтобы найти оптимальные параметры работы системы, поставляем значение q* в соответствующие выражение. Получаем, что оптимальная стратегия
предусматривает заказ q* через каждые |
|
|
|
|
q* |
|
|
t* |
|
2K |
|
|
ν |
|
sν |
единиц времени. Наименьшие суммарные затраты работы системы в единицу времени:
L* 
2Ksν sq*.
108
· · · · · · · · · · · · · · · · · · · · · · · |
Пример 7.1 · · · · · · · · · · · · · · · · · · · · · · · |
Жидкие продукты нескольких видов разливаются в пакеты на одной линии упаковки. Затраты на подготовительно-заключительные операции составляют 700 ден. ед., потребность в продуктах составляет 140 000 л в месяц, стоимость хранения 1 л в течение месяца – 4 ден. ед. Определить оптимальные параметры системы. Сравнить минимальные затраты с затратами при действующей системе разлива одного продукта в течение трех дней.
Решение.
Оптимальные параметры модели Уилсона:
|
|
|
|
|
|
|
|
||
|
q* |
2 700 140 000 |
7 000 (л), |
||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t* |
|
|
2 700 |
|
|
0,05 (месяца) 1,5 (дня), |
|||
|
4 140 000 |
|
|||||||
|
|
|
|
|
|
||||
L* |
|
|
|
28 000 (ден. ед.). |
|||||
|
|
2 700 4 140 000 |
|||||||
При действующей системе tд 3 (дня) |
0,1 (месяца), qд tд ν 14 000 (л). |
||||||||
Величина затрат при действующей системе равна: |
|||||||||
L* 700 140 000 |
4 14 000 |
35 000 (ден. ед.). |
|||||||
|
14 000 |
|
2 |
|
|
||||
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
7.3.2 Модель с конечной интенсивностью поступления заказа
Пусть заказанная партия поступает с интенсивностью u единиц в единицу времени. Очевидно, система может работать без дефицита, если интенсивность поставок u превосходит интенсивность потребления ν. Таким образом рассматривается система типа заводского склада, куда продукция, произведенная одним цехом, поступает с определенной интенсивностью и используется в производстве другого цеха [32]. Изменение уровня запаса для рассматриваемого случая изображено на рисунке 7.4. В течение времени t1 запас одновременно и поступает, и расходуется, это время накопления запаса. В течение t2 запас только расходуется. Длина цикла t t1 t2. Учитывая, что максимальный наличный запас Iм q 1 ν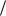
u , издержки системы в единицу времени составят:
L Kν sq |
1 |
ν |
. |
|
u |
||||
q 2 |
|
|