31

3Нелинейное программирование

·· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Вэтом разделе мы рассмотрим задачи нелинейной оптими-

зации (называемые иначе оптимизационными задачами нелиней-

ного программирования), математические модели которых содержат нелинейные зависимости от переменных. Источники нелинейности в задачах подобного типа могут относиться, в частности, к одной из двух категорий [11]:

1.Реально существующие и эмпирически наблюдаемые нелинейные соотношения, например непропорциональные зависимости между объемом производства и затратами, между количеством используемого в производстве компонента и некоторыми показателями качества готовой продукции, между затратами сырья и физическими параметрами (давление, температура и т. п.) соответствующего производственного процесса, между выручкой и объемом реализации и т. п.

2.Установленные (постулируемые) руководством правила поведения или задаваемые зависимости, например правила расчета

спотребителями энергии или других видов услуг, правила определения страховых уровней запаса продукции, гипотезы о характере вероятностного распределения рассматриваемых в модели случайных величин, различного рода договорные условия взаимодействия между партнерами по бизнесу и др.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Вотличие от задачи линейной оптимизации (линейного программирования), не существует одного или нескольких алгоритмов, эффективных для решения любых нелинейных задач. Какой-то алгоритм может быть эффективен при решении задач одного типа и неприемлемым для задач другого типа. В связи с этим разработаны алгоритмы для решения каждого класса (типа) задач. Следует иметь в виду, что даже программы, ориентированные на решение определенного класса задач, не гарантируют правильность решения любых задач этого класса и оптимальность решения следует проверять в каждом конкретном случае.

33

X 2 1 Y 1 3, Y ln X 1 ,

то можно заменить эту задачу задачей минимизации функции:

ванный градиент (вектор единичной длины, составленный из компонент, де-

сбольшим значением функции и приходится еще уменьшать шаг и т. д.

·· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Есть и более эффективные переходы по градиенту, связанные с выбором различного шага по разным координатам или с автоматическим определением шага (при каждом переходе решается задача поиска экстремума функции в заданном направлении). Однако гарантии нахождения глобального экстремума нет (при разных начальных точках или шагах можно получить разные решения для многоэкстремальных функций).

Градиентные методы для задач с ограничениями, где при смещениях по градиенту приходится сталкиваться с опасностью «выскочить» за пределы допустимого множества решений, существенно усложняются (модифицированный метод Ньютона, методы возможных направлений Зойтендейка, сопряженных градиентов, проектируемых градиентов Розена и др.) [13].

34

Существует обширная литература по численному анализу, где значительное внимание уделяется градиентным и другим итерационным методам, но тем не менее решение нелинейных задач оптимизации при наличии ограничений иногда весьма затруднительно.

2. Методы Монте-Карло. Здесь отыскивается n-мерный параллелепипед, включающий в себя множество планов, и затем моделируются N случайных точек с равномерным законом распределения в параллелепипеде (практически во всех программных средах предусмотрено наличие соответствующих датчиков псевдослучайных чисел).

В точках, попавших во множество планов, вычисляются значения функции и запоминается точка текущего экстремума. После этого берется параллелепипед меньших размеров с центром в найденной точке, и в нем вновь моделируются N случайных точек. Процесс такого стохастического моделирования заканчивается при малых размерах параллелепипеда. Методы Монте-Карло имеют преимущество над моделированием на детерминированной сетке, так как их точность имеет порядок 1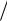N и не зависит от размерности задачи. Естественно, этими методами никто не пользуется при ручном счете; они просты для программной реализации и обычно используются при поиске начального приближения для градиентных методов.

3.Методы динамического программирования, сводящие многомерную задачу оптимизации к последовательности задач меньшей размерности.

4.Методы выпуклого программирования, реализующие поиск миниму-

ма выпуклой функции или максимума вогнутой на выпуклом множестве планов. Если множество планов – выпуклый многогранник, то эти методы допускают использование симплексного метода [14].

Наиболее эффективно эти и другие методы решения действуют для так называемых сепарабельных функций, т. е. функций, представимых в виде суммы функций одной переменной:

F X1, X2,..., Xn f1 X1 f2 X2 ... fn Xn .

При решении многих задач нелинейного программирования определен-

ный эффект дает метод множителей Лагранжа.

Пусть требуется найти экстремумы функции F X при условиях fi X 0 (i 1...m).