13

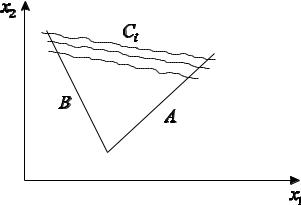
б) детерминированные (А, В) и стохастические (группы кривых Ci )

(рис. 2.2).

Рис. 2.2 – Детерминированные и стохастические ограничения

Стохастические ограничения являются возможными, вероятностными, случайными.

Оптимизационные задачи решаются методами математического программирования, которые подразделяются:

на линейное программирование;

нелинейное программирование;

динамическое программирование;

целочисленное программирование;

выпуклое программирование;

исследование операций;

геометрическое программирование и др.

Главная задача математического программирования – это нахождение экстремума функций при ограничениях в форме уравнений и неравенств.

Рассмотрим оптимизационные задачи, решаемые методами линейного программирования.

2.2 Оптимизационные задачи с линейной зависимостью между переменными

Пусть:

bi – количество ресурса вида i (i 1,2,...,m);

aij – норма расхода i-го ресурса на единицу j-го вида продукции; x j – количество продукции вида j ( j 1,2,...,n);

14

c j – прибыль (доход) от единицы этой продукции (в задачах на мини-

мум – себестоимость продукции).

Тогда оптимизационная задача линейного программирования (ЛП) в общем виде может быть сформулирована и записана следующим образом:

Найти переменные xj ( j 1,2,...,n), при которых целевая функция

n

F(x)= cj xj max (min),

j=1

была бы максимальной (минимальной), не нарушая следующих ограничений:

Вcе три случая можно привести к так называемой канонической форме, введя дополнительные переменные:

n+k

aij xj bi i =1,2,...,m,

j=1

k – количество дополнительных переменных, и условие неотрицательности искомых переменных:

xj 0.

В результате решения задачи находится некий план (программа) работы некоторого предприятия. Отсюда и появилось слово «программирование» [6]. Слово «линейное» указывает на линейный характер зависимости как в целевой функции, так и в системе ограничений. Следует еще раз подчеркнуть, что задача обязательно носит экстремальный характер, т. е. состоит в отыскании максимума или минимума (экстремума) целевой функции.

2.2.1 Геометрическая интерпретация оптимизационных задач линейного программирования

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Графический метод применяется для решения задач с двумя

неизвестными x j , j=1,2. Все условия выражаются в виде линейных

ограничений, и записывается целевая функция Z.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

15

Алгоритм графического метода

Первый шаг при использовании графического метода заключается в геометрическом представлении допустимых решений, т. е. построении области допустимых значений, в которой одновременно удовлетворяются все ограничения модели. Условия неотрицательности переменных x1 0 и x2 0 ограничивают область их допустимых значений первым квадрантом. Другие границы пространства решений изображены на плоскости прямыми линиями, построенными по уравнениям, которые получаются при замене знака на знак = в остальных ограничениях. Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных. В каждой точке, принадлежащей внутренней области или границам многоугольника решений, все ограничения выполняются, поэтому решения, соответствующие этим точкам, являются допустимыми.

Пространство решений содержит бесконечное число таких точек, но, несмотря на это, можно найти оптимальное решение, выяснив, в каком направлении возрастает (или убывает) целевая функция. На график наносят ряд параллельных линий, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях Z, что позволяет определить наклон целевой функции и направление, в котором происходит ее увеличение (уменьшение).

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Чтобы найти оптимальное решение, следует перемещать пря-

мую Z в направлении возрастания (убывания) целевой функции до тех пор, пока она не сместится в область недопустимых решений.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Цех выпускает в смену трансформаторы двух видов. Для их изготовления используются железо и проволока. Общий запас железа – 24 кг, проволоки – 18 кг. На один трансформатор первого вида расходуются 3 кг железа и 3 кг проволоки, а на один трансформатор второго вида – 4 кг железа и 2 кг проволоки. За каждый реализованный трансформатор первого вида завод получает прибыль 4 д. е., второго – 2 д. е.

16

Необходимо составить план выпуска трансформаторов, обеспечивающий заводу максимальную прибыль в смену, если в смену должно выпускаться не более 4 трансформаторов одного вида.

В данной задаче две неизвестные: x1 – выпуск трансформаторов Т1 за смену, x2 – выпуск трансформаторов Т2 за смену.

Ограничения накладываются на запасы железа и проволоки, а также на выпуск трансформаторов Т1 за смену:

3x1 4x2 24,3x1 2x2 18,

x1 4,

x1 0, x2 0.

Целевая функция имеет вид: Z 4x1 2x2 max.

Определяем точки, необходимые для построения множества допустимых значений:

1. 3x1 4x2 24: x1 0 x2 24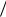4 6, x2 0 x1 24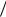3 8.

2. 3x1 2x2 18: x1 0 x2 182 9, x2 0 x1 18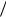3 6.

3. x1 4 x2 – любое значение (вертикальная прямая).

Для построения целевой функции 4x1 2x2 8 (значение Z 8 выбрано произвольно):

x1 0 x2 8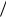2 4, x2 0 x1 84 2.

Из рисунка 2.3 видно, что точкой максимума является точка В (точка пересечения прямых 2 и 3), координаты которой можно определить как решение системы:

3x1 2x2 18,

x1 4.

Подставляя значение x1 4 в первое уравнение системы, получаем значе-

Таким образом, может быть сделан следующий вывод: максимальная прибыль 20 д. е. будет получена при выпуске за смену и реализации 4 трансформаторов Т1 и 3 трансформаторов Т2.