109 |
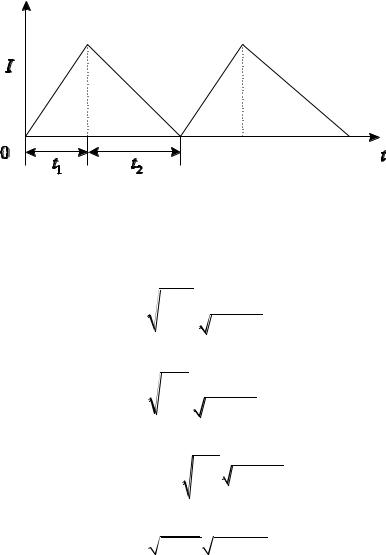
Рис. 7.4 – Модель с конечной интенсивностью поступления заказа
Оптимальные параметры работы системы определяются обычным образом. Величины оптимальной партии:
|
q* |
|
2Kν |
1 |
|
|
|
, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
s |
|
|
1 |
ν / u |
|||||||||||
|
|
|
|
|
|
|
|||||||||||
оптимальный период возобновления заказа: |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
t* |
|
2K |
1 |
|
|
, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
sν |
|
1 ν / u |
|
|
||||||||||
и его составляющие: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t* q* |
|
|
|
|
|||||||||||||
,t* 2K |
|
, |
|||||||||||||||
1 ν / u |
|||||||||||||||||
1 |
u |
2 |
|
|
|
|
sν |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
минимальные издержки в единицу времени:
L* 
2Ksν 
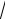1 ν / u.
В случае, когда интенсивность поставки значительно больше интенсивности потребления ν / u 0, расчетные параметры становятся параметрами обычной системы Уилсона.
7.3.3Модель с учетом неудовлетворенных требований
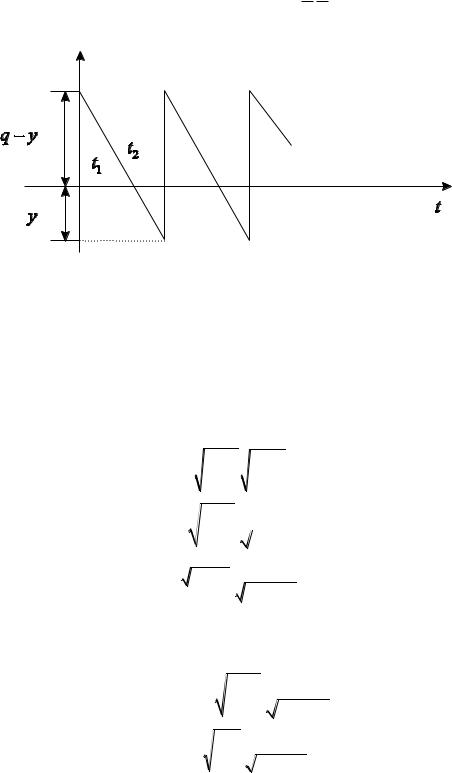
Внекоторых случаях, когда потери из-за дефицита сравнимы с издержками хранения, дефицит допускается. Пусть требования, поступающие в момент отсутствия запаса, берутся на учет. Обозначим через y максимальную ве-
личину задолженного спроса (рис. 7.5). Максимальная величина наличного запаса Y q y расходуется за время t1 (время существования наличного запаса), а затем поступающие требования ставятся на учет в течение времени t2 (время дефицита). При поступлении очередной партии в первую очередь удовлетворяется задолженный спрос, а затем пополняется запас [33]. Убытки, связанные с дефицитом единицы запаса в единицу времени, составляют d. Затра-
110
ты на хранение продукции пропорциональны средней величине запаса q y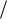 
2
и времени его существования q y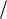 
ν; аналогично убытки от дефицита про-
порциональны средней величине дефицита y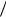
2 и времени его существования y
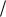ν. Средние издержки работы системы в течение цикла, включающие затраты на размещение заказа, содержание запаса и потери от дефицита:
L K s q y q y d y y . |
||
ц |
2 ν |
2 ν |
|
||
Рис. 7.5 – Модель с учетом неудовлетворенных требований
Разделим издержки цикла на его величину t q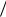
ν и получим издержки работы системы в единицу времени:
L Kν s |
q y 2 d |
|
|
y2 |
. |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
q |
|
|
|
|
|
2q |
|
|
|
|
|
|
|
|
|
|
|
2q |
|
|
|||||||||||||||
Откуда обычным способом находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
q* |
2Kν |
|
|
|
|
1 |
s |
, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
s |
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y* |
s |
|
|
2Kν |
|
|
|
|
1 |
|
|
|
|
|
, |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
d |
|
|
|
|
s |
|
|
|
|
1 s / d |
|
|
||||||||||||||||||||||
|
L* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2Ksν |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 s / d |
|
|
||||||||||||||||||||
Подставив значения q* и y* |
в соответствующие выражения, найдем дру- |
|||||||||||||||||||||||||||||||||||
гие оптимальные параметры системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
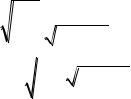
Y* q* y* |
|
2Kν |
1 |
|
|
|
|
|
|
, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
s |
|
|
|
|
|
|
1 s / d |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
t* Y* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2K |
|
|
|
|
1 |
|
|
, |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
ν |
|
|
|
|
sν |
|
|
|
|
|
|
1 s / d |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
111
|
y* |
|
|
|
|
|
|
|
|
|
t* |
|
s |
|
2K 1 |
|
, |
||||
|
|
|
|
|
|
|
|
|||
2 |
ν |
|
d |
|
sν 1 s / d |
|
|
|||
|
|
|
|
|
||||||
t* t* t* q* |
|
2K |
|
. |
||
1 s / d |
||||||
1 |
2 |
ν |
|
sν |
||
|
|
|
||||
Вболее сложных моделях управления запасами сохраняется общий подход: строится функция затрат на приобретение запаса, строится функция потерь при хранении запаса и при его нехватке, находится уравнение, при котором минимизируются затраты и потери.
7.3.4Модель с определением точки заказа
Вреальных ситуациях следует учитывать время выполнения заказа Q.
Для обеспечения бесперебойного снабжения заказ должен подаваться в момент, когда уровень запаса достаточен для удовлетворения потребности на время выполнения заказа. Этот уровень называется точкой возобновления заказа и обозначается j. Для систем, в которых дефицит не допускается, заказ должен размещаться в момент, когда величина наличного запаса равна:
j Qν Q q*,
t*
где [.] – целая часть числа (.).
Для обеспечения бездефицитной работы необходим минимальный начальный запас I0 , величина которого I0 Qν. Пусть I – фактический началь-
ный запас. Для непрерывной работы необходимо, чтобы I Qν. Время потребления начального запаса равно I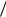
ν. Чтобы заказанная партия была доставлена не позже полного расхода начального запаса, ее нужно разместить в момент T0 I
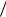ν Q. В общем случае заказы нужно размещать в моменты:
I |
|
|
||
T |
|
Q |
kt*, k 0,1,2,... |
|
ν |
||||
|
|
|
||
В системе с конечной интенсивностью поступления заказа при определении оптимальной точки рассматриваются два случая:
если Q Q t*
t*
если Q Q t*
t*
|
Q |
|
t2*, то t Q ν u |
* |
|
|
t |
|
Q |
|
|
t2*, то t Qν |
* q*. |
|
t |
|
|
1 uν 1 q*;
Для системы с учетом неудовлетворенных требований точка заказа определяется по формуле
112
j Qν Q q* y*
t*
и может быть отрицательной величиной. Это означает, что заявки на пополнение запаса должны посылаться, когда величина дефицита составляет j .
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Контрольные вопросы по главе 7
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
1.Что изучает теория управления запасами?
2.Как классифицируются системы управления запасами?
3.Опишите модель Уилсона.
4.Из чего складываются затраты на закупку товара?
5.Как определить оптимальный объем закупки?
6.Как определить период между поставками?