74
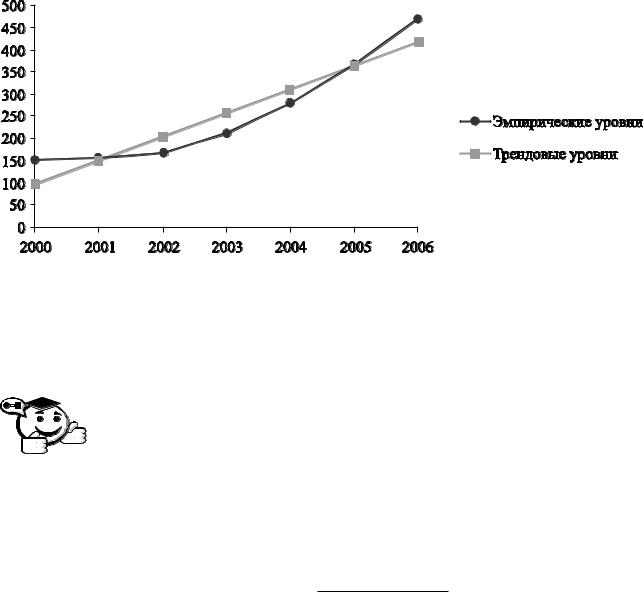
Рис. 5.2 – Эмпирические и трендовые уровни ряда динамики ВО России
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
5.4 Оценка адекватности тренда и прогнозирование
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Для найденного уравнения тренда необходимо провести оценку
его надежности (адекватности), что осуществляется обычно с помощью критерия Фишера, его расчетное значение Fp сравнивает-
ся с теоретическим (табличным) значением FT (прил. В). При этом расчетный критерий Фишера определяется по формуле:
Fp n k yˆt y 2 ,k 1 yˆt y 2
где k – число параметров (членов) выбранного уравнения тренда.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Для проверки правильности расчета сумм для Fp можно использовать
следующее равенство:
y y 2 yˆt y 2 yˆt y 2.
Сравнение расчетного и теоретического значений критерия Фишера ведется при заданном уровне значимости (вероятности сделать неверный прогноз) с учетом степеней свободы: ν1 k 1 и ν2 n k. При условии Fp FT считается,
что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд [27].
75
· · · · · · · · · · · · · · · · · · · · · · · |
Пример 5.10 · · · · · · · · · · · · · · · · · · · · · · · |
В нашем примере про ВО это равенство соблюдается (необходимые суммы рассчитаны в трех последних столбцах таблицы 5.5):
89 410,434 9 652,171 79 758,263.
Проверим тренд на адекватность:
Fp 79 758,263 5 9 652,171 1 = 41,32 FT ,
значит, модель адекватна и ее |
можно использовать для |
прогнозирования |
||||||
F |
6,61 находим по прил. В в |
1-м столбце |
ν k 1 2 1 1 |
и 5-й строке |
||||
|
T |
|
|
|
1 |
|
|
|
|
ν |
2 |
n k 5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Как уже было отмечено ранее, в нашем примере можно произвести выравнивание не только по прямой линии, но и по параболе, чего делать не будем, так как уже найденный линейный тренд адекватно описывает тенденцию.
При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле:
yˆt tασyˆ , |
(5.1) |
где yˆt – точечный прогноз, рассчитанный по модели тренда; tα – коэффициент доверия по распределению Стьюдента при уровне значимости α и числе сте-
пеней свободы ν n 1 (прил. Б)1; σ yˆ – ошибка аппроксимации, определяемая по формуле:
σyˆ |
yˆt y 2 |
. |
|
n k |
|||
|
|
||
· · · · · · · · · · · · · · · · · · · · · · · |
Пример 5.11 · · · · · · · · · · · · · · · · · · · · · · |
||
Спрогнозируем ВО России на 2007 и 2008 гг. с вероятностью 0,95 (значимостью 0,05), для чего найдем ошибку аппроксимации по формуле:
σyˆ 
9652,171
7 2 43,937
1Используется при малом количестве уровней (n < 30), в противном случае (n > 30) вместо tα используют коэффициент доверия t нормального закона распределения (прил. А).
76
и найдем коэффициент доверия по распределению Стьюдента по прил. Б: tα 2,4469 при ν 7 1 6.
Прогноз на 2007 и 2008 гг. с вероятностью 0,95:
Y2007 257,671 53,371 4 2,4469 43,937
или
363,6 Y2007 578,7 (млрд долл.);
Y2008 257,671 53,371 5 2,4469 43,937
или
417,0 Y2008 632,0 (млрд долл.).
Как видно из полученных прогнозов, доверительный интервал достаточно широк (из-за достаточно большой величины ошибки аппроксимации). Более точный прогноз можно получить при выравнивании по параболе 2-го порядка.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Контрольные вопросы по главе 5
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
1.Что такое ряд динамики? Что он характеризует?
2.Какие виды рядов динамики Вы знаете?
3.Назовите цепные и базисные показателя рядов динамики. Как они рассчитываются и что показывают?
4.Назовите средние показатели рядов динамики. Как они рассчитываются и что показывают?
5.Какие Вы знаете методы выравнивания рядов динамики?
6.Что такое тренд и как определить его параметры?
7.Как оценить адекватность тренда?