
7 семестр / Ферменты-2
.pdf
172
Лекция № 21. Ферменты. Кинетика ферментативных реакций
1.Скоростьопределяющие стадии. Ингибирование избытком субстрата
2.Кинетические схемы и уравнение Михаэлиса. Линеризация уравнения.
3.рН-зависимости ферментативных реакций.
4.Зависимость скорости реакций от температуры.
5.Конкурентные и неконкурентные ингибиторы.
6.Аллостерические эффекты. Уравнение Хилла
Кинетика ферментативных реакций
Зависимость скорости ферментативной реакции от концентрации субстрата. Уравнение Михаэлиса-Ментен
Биокинетика начала развиваться в начале XX в., когда несколькими исследователями была изучена скорость ферментативной реакции от концентрации субстрата (Brown, 1892; Brown, 1902; Henri, 1902; Henri, 1903; Michaelis, Menten, 1913). Исследовалась реакция гидролиза сахарозы, катализируемая дрожжевой инвертазой. Эксперименты были поставлены в условиях существенного избытка субстрата по сравнению с концентрацией фермента (рис. 1). Оказалось, что зависимость начальной скорости от концентрации субстрата описывается гиперболической функцией (1):
при этом параметр Vm линейно увеличивается с ростом количества фермента, вводимого в реакцию:
где Е0 — начальная концентрация фермента в произвольных единицах. Для объяснения экспериментально наблюдаемых зависимостей существуют по крайней мере два механизма, различающихся по физической картине явления.
1. Согласно первой модели (схема Михаэлиса) в процессе каталитического действия активный центр фермента с субстратом образуют промежуточный фермент-субстратный комплекс, внутримолекулярное превращение которого приводит к образованию продуктов с регенерацией активного центра:
где k1, k-1 — константы скорости образования и диссоциации ферментсубстратного комплекса; k2 — константа скорости мономолекулярного превращения комплекса.

173
Рис.1. График зависимости скорости ферментативной реакции от концентрации субстрата
Vmax |
k2 [E] - максимальная скорость ферментативной реакции при |
|
полном насыщении фермента субстратом, |
||
K M |
k 1 k2 |
– константа Михаэлиса, |
|
||
|
k1 |
|
[S] – концентрация субстрата.
k1 - константа образования фермент-субстратного комплекса ES, k 1 - константа диссоциации фермент-субстратного комплекса ES.
K M равна концентрации субстрата при скорости ферментативной реакции, равной половине максимальной скорости и характеризует сродство данного фермента к тому или иному субстрату.
Некоторые ферменты требуют высокой концентрации субстрата для достижения скорости, равной максимальной, другие (например,
гексокиназа) достигают Vmax
2
при очень низкой концентрации субстрата.
Таблица.
Значения констант Михаэлиса для некоторых ферментов.
Фермент |
Субстрат |
K M |
|
|
|
каталаза |
H2O2 |
25 |
|
|
|
гексокиназа (мозг) |
D-глюкоза |
0,05 |
|
|
|
|
D-фруктоза |
1,5 |
|
|
|
|
АТФ |
0,4 |
|
|
|
карбоангидраза |
HCO3- |
9 |

174
химотрипсин |
Gly-Tyr-Gly |
108 |
|
|
|
|
N- |
2,5 |
|
бензоилтирозинамид |
|
|
|
|
Vmax - скорость реакции при 250С, оптимальном значении рН, полном насыщении фермента субстратом.
k2 - число оборотов фермента, т.е. число молекул субстрата, которое превращает одна молекула фермента за 1 минуту.
Например: |
|
карбоксиангидраза |
36000000 |
-амилаза |
1100000 |
фосфоглюкомутаза |
1240 |
Линеризация уравнения Михаэлиса-Ментен
Уравнение Михаэлиса-Ментен можно преобразить алгебраическим способом в другие формы, более удобные для анализа экспериментальных данных:
1 K M 1 1
v0 Vmax [S ] Vmax
Механизм Анри
Другой механизм (схема Анри) также включает образование комплекса «фермент—субстрат», однако комплекс нереакционноспособен, а ферментативная реакция протекает бимолекулярно при взаимодействии субстрата с активным центром фермента:
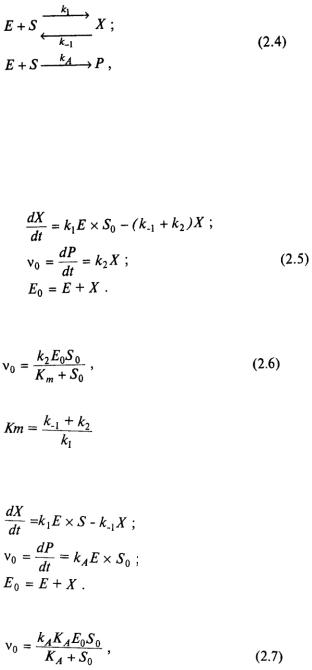
175
где kA — константа скорости второго порядка взаимодействия активного центра фермента с субстратом.
Обе предложенные схемы описывают экспериментально наблюдаемую зависимость начальной стационарной скорости реакции от концентрации субстрата и фермента. Схема Михаэлиса—Ментен при избытке субстрата приводит к следующей системе уравнений:
В условиях стационарности по промежуточному соединению (dX/dt =0) уравнение начальной стационарной скорости имеет вид
где
Соответственно вторая кинетическая схема (схема Анри) описывается отличающейся от (2.5) системой уравнений:
Для нее в стационарном состоянии уравнение скорости имеет вид
где КA = k-1/k1
На основе экспериментальных данных в стационарном режиме схемы (2.3) и (2.4) неотличимы, поскольку приводят к одному и тому же уравнению скорости. Дискриминировать эти механизмы из данных по стационарной кинетике реакции невозможно. Существовало мнение, что кинетические методы в этом случае бессильны и вообще невозможно доказать справедливость того или иного механизма реакции.
эти механизмы могут быть дискриминированы при изучении протекания реакции во времени, в режиме, предшествующем образованию стационарного состояния.
Рассмотренные механизмы имеют лишь историческое значение. В настоящее время неизвестны ферменты, которые действовали бы по простой схеме (2.3) или (2.4). Как правило, реальные механизмы включают большое число

176
промежуточных соединений фермента с субстратом, их идентификация, исследование структуры, скоростей образования и расхода и составляют предмет изучения механизмов ферментативных реакций.
Несмотря на то, что схема и уравнение Михаэлиса не соответствует на молекулярном уровне ни одному механизму реакции, использование этого уравнения получило большое распространение. Это одно из фундаментальных уравнений ферментативной кинетики. Уравнение Михаэлиса феноменологически описывает практически все ферментативные реакции, а наблюдаемые отклонения, как правило, связаны с усложнением простейшей схемы. Дело в том, что уравнение Михаэлиса отражает фундаментальную особенность ферментативных реакций — участие в механизме процессов лабильных промежуточных соединений субстрата и активного центра фермента.
Все кинетические схемы, включающие стадии образования и расхода промежуточных соединений, приводят к зависимости скорости от концентрации субстрата типа уравнения Михаэлиса.
НАСКОЛЬКО СХЕМА МИХАЭЛИСА ЕДИНСТВЕННА?
Может быть, существуют и другие кинетические схемы к той же самой зависимости скорости реакции от концентрации субстрата?
Число кинетических схем, приводящих к зависимости скорости реакции от концентрации субстрата, неограниченно велико.
Таблица 1
Некоторые кинетические схемы, приводящие к уравнению стационарной скорости, эквивалентному уравнению Михаэлиса
В табл. 1 даны некоторые простейшие кинетические схемы, приводящие к уравнению начальной стационарной скорости, формально эквивалентному уравнению Михаэлиса.
Может быть, существуют и другие кинетические схемы к той же самой зависимости скорости реакции от концентрации субстрата?

177
Число кинетических схем, приводящих к зависимости скорости реакции от концентрации субстрата, неограниченно велико.
Несмотря на кажущуюся сложность реакции, вне зависимости от числа и природы интермедиатов, принимающих участие в механизме реакции, стационарная кинетика процесса будет описываться уравнением Михаэлиса. Для характеристики ферментативных реакций обычно определяют оба параметра, входящие в уравнение Михаэлиса-Ментен: максимальную скорость Vm и константу Михаэлиса Кm.
Важно отметить, что без детального знания механизма реакции интерпретация kкат и Кm как констант связывания фермента субстратом и константы скорости превращения фермент-субстратного комплекса неправильна, поскольку для разных кинетических схем константы kкат и Кm могут отражать совершенно различные процессы (см. табл. 1), тем не менее эти характеристики легко определяются экспериментально и в ряде случаев несут весьма важную информацию о свойствах каталитической реакции.
Вкачестве иллюстрации положения о существовании множества кинетических схем, приводящих к уравнению Михаэлиса рассмотрим стационарную кинетику фермент-субстратного превращения в более общем случае — для системы с участием произвольного числа — n-промежуточ- ных соединений
Встационарном состоянии по промежуточным соединениям (dXi/dt = = 0,i = 2,n) и при избытке субстрата (S0>>Ε0) кинетику процесса описывает система уравнений:
Для реакции (2.12) зависимость начальной стационарной скорости процесса от концентрации субстрата будет иметь вид уравнения Михаэлиса:
где значения kкат и Кm имеют эффективный характер и заданы уравнениями

178
Скоростьопределяющие стадии
Большинство экспериментальных кинетических исследований ферментов выполнено в режиме стационарной кинетики в условиях, когда скорость изменения концентраций лабильных интермедиатов существенно ниже скоростей образования продуктов или расхода субстратов. Как правило, постановка экспериментов в стационарном кинетическом режиме не вызывает сложностей. При этом из данных стационарной кинетики получают принципиально важную информацию о скоростях лимитирующих стадий ферментативных реакций.
Максимальная скорость ферментативной реакции характеризует самый медленный кинетический процесс (или группу самых медленных процессов), протекающий в активном центре катализатора. Действительно,.из рассмотренной выше кинетической схемы реакции с участием произвольного числа n лабильных интермедиатов следует, что если существует какая-либо реакция, характеризуемая наименьшим значением константы скорости k1 [см. схему (2.12) и уравнение (2.14)], то эта константа будет определять величину
максимальной скорости реакции. Если ki<<kj, j = 2, ..., η, j i, το kкат= ki. Поскольку лимитирующие процессы представляют наибольший интерес,
информацию, получаемую методами стационарной кинетики, трудно переоценить.
С другой стороны, существуют достаточно большие сложности в интерпретации стационарно-кинетических данных. Идентификация лимитирующих стадий реакции — одна из наиболее сложных задач в исследовании механизмов действия ферментов. Рассмотрим несколько подходов для определения лимитирующей стадии реакции.
1. Использование субстратов с различной структурой и различной реакционной способностью. Если заметно различающиеся субстраты характеризуются одним и тем же значением kкат с высокой степенью достоверности, можно утверждать, что реакция включает образование промежуточного соединения, структура которого является общей для всех исследованных субстратов, и превращение этого интермедиата лимитирует скорость каталитического процесса. Например, изучение гидролиза протеолитическими ферментами различных эфиров общей формулы
где структура R была постоянной, а варьировалась природа уходящей группы R', показало, что определяемое из данных стационарной кинетики значение Vm(kкат) практически не зависит от структуры радикала R, в то время как реакционная способность, эфиров в реакции щелочного гидролиза различается очень сильно [Дженкс, 1972]. Это -химотрипсином и позволило авторам предположить, что в реакции гидролиза папаином сложноэфирных субстратов образуется промежуточное ацилферментное соединение; гидролиз этого интермедиата является скоростьопределяющей стадией.

179
В дальнейшем это предположение было проверено независимыми экспериментами: 1) исследовалась кинетика реакции в присутствии добавленных низкомолекулярных реагентов, ускоряющих, гидролиз ацилфермента; 2) некоторые ацилферментные промежуточные соединения, относительно стабильные при кислых значениях рН, были выделены в индивидуальном виде и идентифицированы; 3) была исследована предстационарная кинетика реакции и детально изучена кинетическая схема процесса методами быстрокинетических измерений, позволяющих детектировать кинетику образования и расхода ацилфермента.
Проанализируем численные значения каталитических констант скоростей и констант Михаэлиса различных ферментов, с тем чтобы представить «средние» скорости реакций в биохимических системах. Был проведен статистический анализ констант kкат и Кm ферментных систем, для которых измерены к настоящему времени значения kкат и найдены плотности распределения ферментов по значениям каталитических констант. С этой целью ферменты были разбиты на группы приблизительно с одинаковыми (в пределах одного порядка) константами процесса, определялось число ферментов в группе и полученные значения нормировались к общему числу ферментов в выборке.
На рис. 2.6 приведены плотности распределения ферментов по величине kкат и Km. Кривые, представленные на этом рисунке, отражают вероятность того, что каждый случайно выбранный фермент будет характеризоваться заданным значением параметра. Так, вероятность того, что какой-либо неизвестный фермент имеет значение kкат=102 c-1, 0,5. Путем весьма высока интегрирования плотности распределения могут быть вычислены вероятности того, что выбранный наугад фермент будет обладать кинетическими характеристиками в заданном диапазоне.
Рис. 2.. Плотности распределения ферментов по кинетическим (а) и равновесным (б) параметрам.
Из рис. 2. видно, что наиболее распространены ферменты, у которых константы скорости лимитирующих стадий реакций имеют порядок 102 с-1, Кm~ 10-4 Μ. Ферменты весьма унифицированы по каталитическим характеристикам. Энергетический барьер 8—15 ккал/моль, проявляющийся на лимитирующих стадиях ферментативных реакций и приводящий к «числу оборотов» активных центров ~ 102 с-1, обусловлен, по-видимому, рядом физико-химических эффектов.

180
Другие типичные зависимости начальной стационарной скорости реакции от концентрации субстрата
Ранее была приведена наиболее распространенная зависимость начальной стационарной скорости реакции от концентрации субстрата. Эта зависимость
описывается уравнением Михаэлиса: 
иявляется отражением участия интермедиатов в процессе конверсии субстрата в активном центре фермента. При низких концентрациях субстрата
(S0 << Кm) скорость реакции имеет первый порядок по каждому из реагирующих веществ и суммарный второй порядок.
иотражает стадию взаимодействия субстрата с активным центром фермента. Наблюдаемая константа скорости имеет вид
kнабл (S0 << Km) = kкат/Km
При больших «насыщающих» концентрациях субстрата скорость отражает какой-либо мономолекулярный процесс, протекающий в активном центре фермента после взаимодействия с субстратом:
v0(S0 >> Km) = kкатE0.
Графически зависимость v0(S0) для «классического» случая приведена на рис. 3 (кривая а).
Рис. |
3. |
Различные |
Известны |
|
виды |
зависимости |
также |
и |
|
начальной |
скорости |
|
другие |
|
зависимости. Экспериментально наблюдаются зависимости скорости реакции от концентрации субстрата с экстремумом (рис. 3, кривая б) или с ускорением на начальном этапе (рис. 3, кривая в). За каждым из этих случаев стоит соответствующий механизм, который приводит к тому или иному типу зависимости. Для этих реакций уравнение Михаэлиса—Ментен не описывает экспериментально наблюдаемой зависимости скорости от концентрации субстрата. Эти случаи связаны со значительными изменениями в механизме реакции и, как правило, вызывают интерес исследователей, поскольку эффекты такого рода имеют большое регуляторное значение. Известно несколько механизмов, приводящих к «немихаэлисовым» зависимостям скорости реакции. Все эти механизмы связаны с взаимодействием с ферментом нескольких молекул субстрата. Отклонения могут быть вызваны ингибированием или активацией реакции избытком субстрата, а также аллостерическими эффектами.

181
Ингибирование и активация избытком субстрата. Кривые с максимумом
Ингибирование субстратом приводит к экстремальной зависимости скорости от концентрации субстрата (рис. 4, кривые a и б). Экспериментально активация субстратом проявляется в увеличении скорости реакции при повышенных концентрациях субстрата (рис. 4, кривые в и г).
Рис. 4. Зависимости начальной скорости ферментативной реакции от концентрации субстрата для случаев ингибирования (а, б) и активации (в, г) фермента избытком субстрата.
Оба этих эффекта обычно объясняют образованием тройного комплекса фермент-субстрат-субстрат, отличающегося по реакционной способности от фермент-субстратного комплекса:
Аллостерические эффекты. Уравнение Хилла. Модель Моно— Уаймена—Шанжѐ
Большое внимание исследователей привлекали достаточно часто наблюдаемые отклонения от уравнения Михаэлиса, приводящие к сигмоидальной зависимости скорости реакции (степени насыщения) от концентрации субстрата. Впервые модель, приводящая к сигмоидальной кривой, была рассмотрена в 1909 г. Хиллом при интерпретации зависимости «насыщения» гемоглобина кислородом от парциального давления кислорода. На рис. 2.14 приведена типичная экспериментально наблюдаемая зависимость. По своей физической сущности функции степени насыщения гемоглобина кислородом и насыщения фермента субстратом полностью эквивалентны и могут рассматриваться в рамках одного подхода.
Принципиальным для объяснения сигмоидальной кинетики является предположение о кооперативном взаимодействии нескольких частиц, приводящих к образованию реакционноспособного состояния активного центра. Для этого необходимо предположить наличие некоего механизма влияния частиц друг на друга. Простейшим является предположение о
