2 курс ОАУ(ТАУ) [препод. Петунин В.И.] / Лекции / 1 (1)

Неоднозначность характеристик связана с зависимостью выходной переменной z не только от мгновенного значения входной переменной x1 но и от предшествующего процесса (гистерезис), поэтому неоднозначные характеристики обычно называют

гистерезисными или с гистерезисом.

Непрерывность. Если функция z(x) не имеет разрывов, то характеристику называют непрерывной. При наличии разрывов функции z(x) характеристику называют разрывной.

Рассмотрим наиболее распространенные типовые звенья, характеристики которых при соответствующих упрощениях симметричны относительно начала координат (нечетносимметричные) и могут быть достаточно хорошо представлены кусочно-линейными кривыми.

Звенья, встречающиеся реже, характеристики которых носят более сложный характер, будем относить к нетиповым, или особым, звеньям. К особым звеньям также будем относить искусственно создаваемые нелинейности, удовлетворяющие определенным задаваемым требованиям.

1.4. Типовые нелинейные звенья

Типовые нелинейные звенья имеют как однозначные, так и неоднозначные характеристики. Эти характеристики могут быть всегда приведены к нормированному безразмерному виду путем изменения масштаба входной x и выходной z величин. Если

нормированную нелинейную характеристику ζ(ξ) в относительных единицах. Описанному преобразованию соответствуют структурные схемы, показанные на рис. 1.5, а, в. На них xakx 1 и xak kz. Типовые нелинейные звенья и их нормированные характеристики были введены Л. С. Гольдфарбом в 1947 г. для приближенного анализа различных систем автоматического регулирования.

Рассмотрим основные нелинейные звенья, описывающие наиболее типичные нелинейности автоматических систем.

18

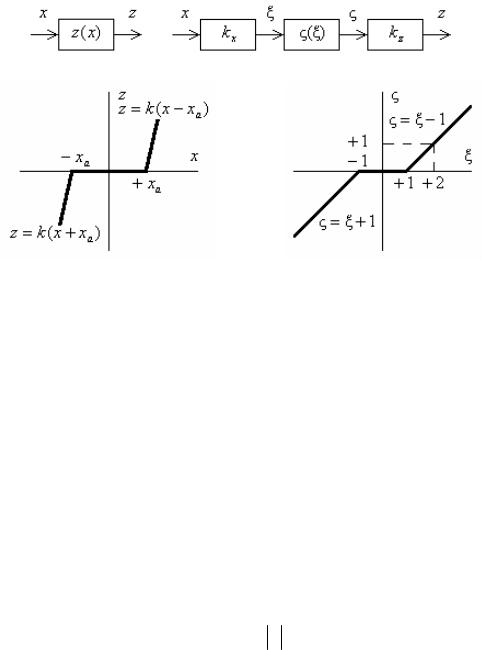
1.4.1. Звенья с однозначными непрерывными характеристиками. К таким звеньям относятся: звено типа «зона нечувствительности», звено типа «ограничение или насыщение», звено типа «ограничение с зоной нечувствительности».

Рис. 1.5

Звено типа «зона нечувствительности». Характеристики звена типа «зона нечувствительности» показаны на рис. 1.5, б, г. Такими характеристиками обладают некоторые схемы электронных, магнитных и гидравлических усилителей в области малых входных сигналов. Простейшей механической моделью зоны нечувствительности является система соединения двух валов с пружинным возвратом ведомого вала в нейтральное положение при наличии участка свободного хода (люфта) в системе передачи. Здесь зона свободного хода ведущего вала имеет ширину 2xa. Характеристика звена (рис. 1.5, б) выражается следующими уравнениями:

0при x xa;

нормированную характеристику

19

0при 1;

1при 1.

Звено типа «ограничение или насыщение». Характеристики звена типа «ограничение или насыщение» показаны на рис. 1.4, г, з. Подобными характеристиками обладают практически все реальные усилители (электронные, магнитные, пневматические, гидравлические), ограниченные по мощности в области больших входных сигналов. Примером простейшей механической модели ограничения является система соединения двух валов через упругую пружину при наличии ограничений или упоров в системе ведомого вала. Здесь зона рабочего хода ведомого вала имеет ширину 2zb.

Характеристика этого звена (рис. 1.6, а) выражается следующими уравнениями:

а б

Рис. 1.6

Звено типа «ограничение с зоной нечувствительности».

Многие элементы системы регулирования описываются нелинейной зависимостью, обладающей как зоной нечувствительности, так и

20

ограничением. Характеристика звена, сочетающего оба этих типа нелинейностей, показана на рис. 1.6, б. При малых входных сигналах оно ведет себя подобно звену типа «зона нечувствительности», а при больших сигналах – подобно звену типа «ограничение».

Характеристика звена описывается следующими уравнениями:

«трехпозиционное реле без гистерезиса», звено типа «аналогоцифровой преобразователь без гистерезиса».

Звено типа «двухпозиционное реле без гистерезиса».

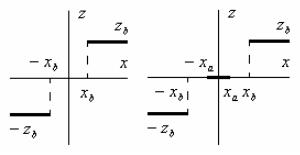
Однозначная характеристика двухпозиционного поляризованного реле показана на рис. 1.7, а. При модуле входного сигнала x xb,

например, контакты реле разомкнуты и о величине напряжения z, снимаемого с контакта реле, ничего сказать нельзя.

Величина z не связана с значением входного сигнала x: и в этом диапазоне изменения x: не существует зависимости z(x). При x xb в зависимости от знака x величина z принимает значение zb

или zb и функция z(x) может быть выражена с помощью знаковой функции. Таким образом характеристика нелинейного звена во всем диапазоне изменения x выражается следующим образом:

21

а б

Рис. 1.7

Звено типа «трехпозиционное реле без гистерезиса».

Однозначная разрывная характеристика трехпозиционного поляризованного реле без гистерезиса показана на рис. 1.7, б.

Аналитически эта характеристика может быть выражена следующим образом:

При анализе и синтезе различных релейных систем управления очень часто пользуются идеализированными характеристиками двухпозиционного реле. Такая характеристика может быть получена путем предельного перехода одной из характеристик, показанных на рис. 1.6, а, б или 1.7, а, б, при xa 0 и xb 0. Однако полученные таким образом в результате предельного перехода характеристики при x 0 имеют различные значения.

Производя аналогичный предельный переход в уравнении (1.11) получим:

22

Для уравнений (1.9) и (1.12) предельный переход дает:

При анализе релейных систем с обратной связью необходимо обращать внимание на различие условий поведения системы при x 0, получаемых в каждом из этих трех случаев. В дальнейшем под нелинейностью типа sign будем понимать характеристику, выражаемую уравнением (1.13).

Эта характеристика может быть аналитически выражена параболой нечетной степени 2n 1 при n :

Обратную зависимость x(z) будем обозначать:

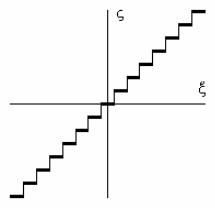
Звено типа «аналого-цифровой преобразователь без гистерезиса». К числу звеньев с однозначными разрывными характеристиками относится звено со ступенчатой характеристикой, преобразующее аналоговую величину в дискретную с квантованием по уровню.

Такая характеристика показана на рис. 1.8. Аналитически она может быть выражена следующим образом:

аналоговый сигнал в цифровую вычислительную машину.

При учете влияния скачков x на движке реостата в потенциометрических приборах при переходе движка от одного витка к другому получим аналогичную зависимость между положением движка и снимаемым напряжением.

Величина скачка напряжения u0 равна напряжению на одном витке реостата. В этом случае:

23

где – толщина провода реостата.

Рис. 1.8

1.4.3. Звенья с двузначными характеристиками. К таким звеньям относятся: звено типа «двухпозиционное реле с гистерезисом», звено типа «трехпозиционное реле с гистерезисом».

Звено типа «двухпозиционное реле с гистерезисом».

Рассмотренные выше однозначные релейные характеристики соответствуют некоторой идеализации реальных систем. В действительности обычно величина входного сигнала, при котором происходит скачок выходной величины z, бывает различной для переключения контакта в прямом и обратном направлениях. Например, в двухпозиционном поляризованном реле при его симметричной регулировке переключение контакта в одном направлении происходит при некотором напряжении, а переключение в обратном направлении – при таком же напряжении противоположного знака. Характеристика двухпозиционного реле показана на рис. 1.9, а.

Математически она выражается следующим образом:

быть записаны условия скачкообразного перехода с верхней ветви на

24

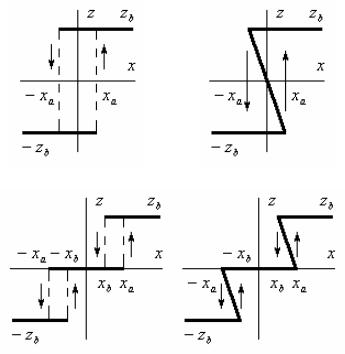
нижнюю: x xa , z zb, dx/dt 0. Свойствами релейного элемента с характеристикой двухпозиционного реле обладают охваченные положительной обратной связью усилители с характеристикой типа ограничение (см. рис. 1.6, б); В этом случае характеристика имеет вид непрерывной ломаной кривой (рис. 1.9, б).

а б

в г

Рис. 1.9

Участок характеристики при xa x xa для zb z zbимеет отрицательный наклон и обычно неустойчив. Таким образом, хотя при xa x xa каждому значению x и соответствуют три значения z, только два из этих значений zb и zb отвечают устойчивому состоянию схемы и, следовательно, характеристика (рис. 1.9, б) сводится к рассмотренной ранее двузначной разрывной характеристике (рис. 1.9, а).

Эквивалентность рассматриваемых двух видов характеристики может быть использована при анализе релейных автоматических систем.

Звено типа «трехпозиционное реле с гистерезисом». При учете различия в значениях входной величины, соответствующих переключениям контактов в одном и другом направлениях,

25

характеристики трехпозиционного реле приобретают неоднозначный характер. Так, если переход от z 0 к z zb происходит при x xa, а возврат – при x xb, то характеристика приобретает вид, показанный на рис. 1.9, в. Математически она выражается так:

На участках xb | x| xa величина z имеет два значения. Аналогичная характеристика получается при охвате усилителя с

зоной нечувствительности и ограничением (см. рис. 1.6, б) положительной обратной связью. В этом случае непрерывная характеристика (рис. 1.9, г) имеет два участка с отрицательным наклоном, которые обычно оказываются неустойчивыми и соответствуют зоне скачка. При учете скачкообразных переходов в характеристике получаем условия ее эквивалентности характеристике трехпозиционного реле с гистерезисом.

Для получения характеристики, изображенной на рис. 1.9, в, может быть применена электрическая схема, состоящая из двух электромагнитных реле Р1 и Р2, включенных через вентили В1 и В2. Контакты реле Р1 и Р2 замыкают цепь между источником питания c напряжением zb и выходными зажимами так, что в зависимости от значения x напряжение z на зажимах принимает значение zb, 0 или

zb в соответствии с характеристикой (рис. 1.9 в).

1.4.4.Звенья с многозначными характеристиками. К таким звеньям относятся: звено типа «люфт», звено типа «упор», звено типа «магнитный гистерезис».

Звено типа «люфт». Одна, из нелинейностей, наиболее часто встречающихся в механических системах, связана с наличием зазоров в системе передачи. Если в механической модели нелинейности типа «зона нечувствительности» убрать пружину, стремящуюся возвратить ведомый вал в нулевое положение, то получится модель нелинейности типа «люфт».

В этом случае зависимость между положением ведущего x и ведомого z валов неоднозначна. Характеристика, выражающая зависимость между положениями ведущего и ведомого валов,

26

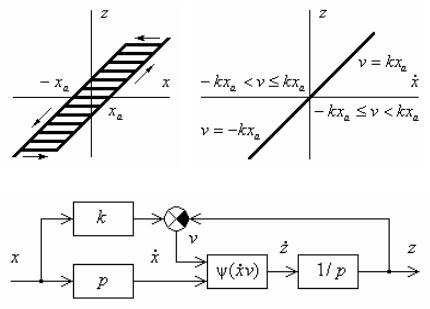
показана на рис. 1.10, а. Каждому положению ведущего вала x соответствует множество положений ведомого вала z, лежащее в пределах k(x xa) z k(x xa). Выбор того или иного из возможных положений определяется максимальным или минимальным отклонением z, предшествовавшим рассматриваемому моменту времени.

в

Рис. 1.10

Аналитически характеристика звена типа «люфт» выражается следующим образом:

Зависимость z от x, выражаемая уравнением (1.22), для различных значений v показана на рис 1.10, б.

Вводя обозначение (x,v) для звена, преобразующего сигналы x и v в сигнал z, можно для звена типа «люфт» получить структурную схему (рис. 1.10, в).

27