
Сборник задач
.pdf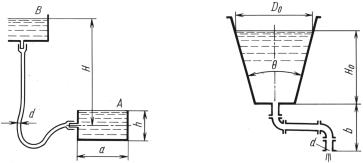
стрее, чем через отверстие такого же диаметра. Начальное заполне- |
|||||||
ние бака Н0 = 4 м, |
диаметр отверстия d = 60 мм, |
его коэффициент |
|||||
расхода μ = 0,6. |
|
|
|
|
|
||
|
Коэффициент сопротивления трения в трубе принять λ = 0,03. |
||||||
|
Ответ. z = 1,65 |
м. |
|
|
|
|
|
|
Задача 11.4. Призматический бак А со стороной квадратного |
||||||
основания a |
= 2 |
м и высотой h |
= 1,6 м заполняется бензином |
||||
из центрального бензохранилища |
В, |
уровень в котором постоянен |
|||||
(H = 5 м). |
Заполнение происходит через гибкий шланг длиной |
||||||
l = 7 м, выходное сечение которого находится на середине высоты |
|||||||
бака. |
|
|
|
|
|
|
|
|
Определить диаметр шланга d, при котором бак будет запол- |
||||||
няться в заданное время Т = 15 мин, приняв коэффициент сопро- |
|||||||
тивления трения в шланге λ = 0,05; местными потерями в шланге |
|||||||
пренебречь. |
|
|
|
|
|
|
|
|
Ответ. d = 50 мм. |
|
|
|
|
||
да |
Задача 11.5. Определить время опорожнения конического сосу- |
||||||
(θ = 30◦) |
|
, |
|
|
d = 15 |
мм и суммарный |
|
|
через трубу диаметр которой |
|
|||||
коэффициент сопротивления ζ = 2,5. |
= 0,85 м, D0 = 1 м, верти- |
||||||
|
Начальный уровень жидкости Н0 |
||||||
кальноемрасстояние от выходного отверстия трубы до дна сосуда
b = 0,6 .
Ответ. Т = 15 мин 50 с.
К задаче 11.4 |
К задаче 11.5 |
Задача 11.6. Из емкости, имеющей постоянное по высоте сече- |
|
ние площадью F = 20 м2, жидкость откачивается насосом с посто- |
|
янным расходом Qн = 4 |
л/с, а также вытекает в атмосферу по гори- |
|
331 |
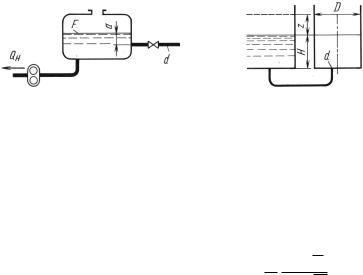
зонтальной трубе диаметром d = 50 мм, |
суммарный коэффициент |
||||||||||
сопротивления которой ζ = 5. |
|
|
|
||||||||
где |
Определить время понижения уровня на величину а = 1 м. |
||||||||||
Ответ. T = μf2√2g √a − √H0 ln 1 + rH0 |
|
= 52 мин, |
|||||||||
|
|
F |
|
|
|
|
a |
|
|
||
|
|
pH0 = μf√н2g и f = |
π4 . |
|
|
||||||
|
|
|
|
|
|
Q |
d2 |
|
|
||
Задача 11.7. Бак диаметром D = 600 мм заполняется водой из |
|||||
резервуара с постоянным уровнем Н = 1,2 м. |
мм, сум- |
||||
Заполнение происходит через трубу диаметром d = 25 |
|||||
марный коэффициент сопротивления которой ζ = 8. |
|
||||
1. |
Определить время заполнения бака до уровня в резервуаре. |
||||
2. |
На какую высоту z следует поднять уровень в резервуаре, что- |
||||
бы бак заполнялся на ту же высоту |
Н в 2 раза быстрее? |
|
|||
Ответ. 1. Т = 14 мин 15 с. 2. z = |
|
9H |
. |
|
|
16 |
|
||||
|
|
|
|
||
К задаче 11.6 К задаче 11.7
Задача Определить время опорожнения целиком запол ненного шарового11.8. сосуда радиусом R = 0,8 м через отверстие диа- метр которого d = 50 мм коэффициент расхода μ = 0,62 Давле, - ние на свободной0 поверхности( жидкости считать атмосферным). . - За какое время из сосуда вытечет половина содержащегося в нем
объема воды?
√
Ответ. Время полного опорожнения T1 = 16 D2 √D = 500 с и половинного T2 = 192 с. 15 μd20 2g
332
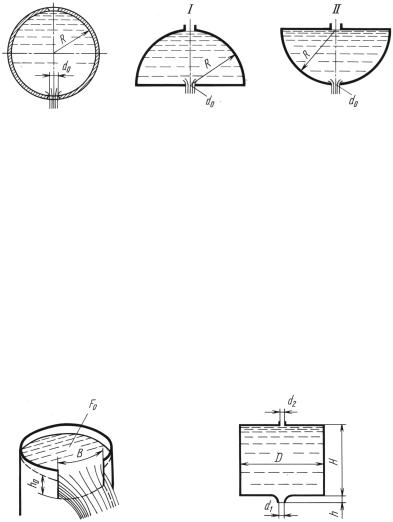
К задаче 11.8 |
К задаче 11.9 |
|||||
Задача 11.9. |
Сравнить время опорожнения полушарового сосу- |
|||||
да радиусом R, |
расположенного сферой вверх (I) и сферой вниз |
|||||
(II). В обоих случаях истечение происходит через одинаковое от- |
||||||
верстие диаметром d0 (коэффициент расхода отверстия принимать |
||||||
постоянным). Давление на свободной поверхности жидкости при |
||||||
истечении считать атмосферным. |
||||||
Ответ. |
TI |
= |
|
12 |
. |
за какое время из резервуара площа- |
|
|
|||||
|
TII |
7 |
|
|||
Задача 11.10. Определить, |
||||||
дью F0 = 300 м2 |
через прямоугольное водосливное отверстие в бо- |
|||||
ковой стенке шириной B = 1,6 |
м выльется объем воды W = 330 м3, |
|||||
если начальный уровень воды над порогом м Коэффициент расхода водослива принятьh0 = 1,2 .
Ответ. Т = 7,9 мин. m = 0,4.
|
|
К задаче 11.10 |
К задаче 11.11 |
|
|
Задача 11.11. Определить время опорожнения целиком за- |
|||
полненного цилиндрического сосуда через сопло (d1 |
= 25 мм, |
|||
μ1 |
= |
0,97), если в верхней крышке сосуда имеется отверстие |
||
(d2 |
= 3 |
мм, μ2 = 0,6), через которое засасывается воздух по мере |
||
вытекания воды. Диаметр сосуда D = 1,2 |
м, его высота |
Н = 1,5 м, |
||
плотность воздуха ρвозд = 1,2 кг/м3. |
|
|
||
|
|
|
|
333 |

Задачу решать исходя из равенства объемных расходов воды и воздуха пренебрегая сжимаемостью последнего Высотой сопла пренебречь, . h
Указание. . Дифференциальное уравнение процесса истечения
|
|
|
|
|
|
|
|
|
dt = − |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dz, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в котором расход воды |
Qвод |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вод |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Qвод = μ1f1s2g |
|
|
|
|
pат |
px |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
z − |
|
|
ρ |
−g |
|
|
|
, |
|
|
|
|
|
|
||||||||||||||||||||
где рат – атмосферное давление; px – |
абсолютное давление воздуха в со- |
|||||||||||||||||||||||||||||||||||||
суде. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из условия равенства в каждый момент времени объемных расходов |
||||||||||||||||||||||||||||||||||||||
воды и воздуха получаем |
|
|
|
|
−g |
|
|
|
= μ2f2s2 |
|
ρ− |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
μ1f1 = s2g z − |
|
ρ |
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
pат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
px |
|
|
|
|
|
|
|
|
pат |
px |
|
|
|
|
||||||||||||
Ответ |
|
|
|
|
|
|
|
|
|
вод |
|
|
|
|
|
|
|
|
|
|
|
возд |
|
|
|
мин |
|
|||||||||||
|
|
μ1√2g d1 |
s |
|
|
μ22d24 ρвод |
|
|
|
|
|
ч |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
D |
|
|
2 |
|
|
|
μ12d14 |
ρвозд |
|
√ |
|
= 1 |
|
|
|
|
|||||||||||||
|
. |
T = |
|
|
|
|
|
|
|
|
|
|
1 + |
|
|
|
|
|
|
|
H |
|
27 |
|
. |
|||||||||||||
Задача 11.12. |
Сосуд с переменным по высоте сечением опорож- |
|||||||||||||||||||||||||||||||||||||
няется через донный сходящийся насадок. |
|
|
|
|
|
|
R от высоты |
|||||||||||||||||||||||||||||||
1. Какой должна быть зависимость радиуса сосуда |
||||||||||||||||||||||||||||||||||||||
сечения z |
над насадком, |
чтобы опускание уровня жидкости проис- |
||||||||||||||||||||||||||||||||||||
ходило равномерно? |
|
|
|
насадка, при котором постоянная ско- |
||||||||||||||||||||||||||||||||||
2. Определить диаметр d |
||||||||||||||||||||||||||||||||||||||
рость опускания уровня в сосуде такой формы будет v = 1 мм/с, |
||||||||||||||||||||||||||||||||||||||
если начальные значения радиуса и заполнения сосуда R0 = 125 мм |
||||||||||||||||||||||||||||||||||||||
и z0 = 310 |
мм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент расхода насадка принимать постоянным и рав- |
||||||||||||||||||||||||||||||||||||||
ным μ = 0,95. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ. |
1. R = A√4 z, где A = r4 |
|
|
. |
|
2. d = 5,15 мм. |
|
|
||||||||||||||||||||||||||||||
|
μ8v2 |
|
|
|
||||||||||||||||||||||||||||||||||
334 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2d4g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
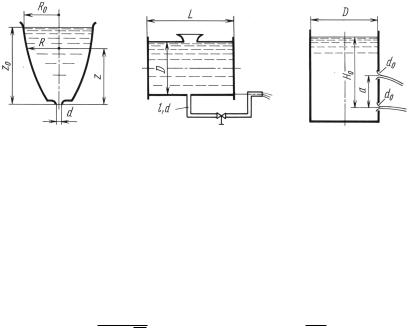
Задача 11.13. Открытая цистерна диаметром D = 2,4 м и дли- |
||||
ной L = 6 м, целиком заполненная бензином, опорожняется через |
||||
сливную трубу, диаметр и длина которой d |
= 50 мм и l = 7 м, а |
|||
выходное сечение находится на уровне нижней точки сечения ци- |
||||
стерны. Суммарный коэффициент местных сопротивлений в трубе |
||||
ζ = 8, коэффициент сопротивления трения λ = 0,025. |
||||
Определить время опорожнения цистерны. |
4 . |
|||
Ответ. T = 3μf√2g |
= 3 ч 21 мин 30 с, где f = |
|||
4LD√D |
|
|
πd2 |
|
Задача 11.14. Определить время опорожнения цилиндрическо- |
||||
го резервуара, диаметр которого |
D = 0,8 м, через два круглых от- |
|||
верстия одинакового диаметра d0 |
= 10 мм, расположенных друг от |
|||
друга на расстоянии а |
= 0,5 м по высоте. |
Начальное положение |
||
уровня H0 = 1,5 м. |
|
|
|
|
Коэффициент расхода каждого из отверстий μ = 0,62. |
||||
Ответ. Т = 1 ч 20 мин. |
|
мм заполняется водой |
||
Задача 11.15. Бак диаметром D = 600 |
||||
К задаче 11.12 |
К задаче 11.13 |
|
К задаче 11.14 |
|
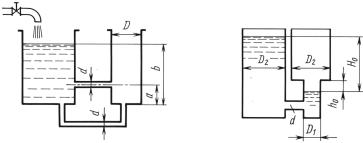
из резервуара с постоянным уровнем b = 1,5 м через две короткие трубы одинакового диаметра d = 25 мм Одна из труб примыкает к дну бака, другая – к его боковой стенке .на высоте а = 0,6 м от дна.
Определить время заполнения бака до уровня в резервуаре учи тывая в трубах только местные потери коэффициент сопротивле, - ния каждого из колен ζ = 1,2; коэффициент( сопротивления входа-
ζ = 0,5).
Ответ. Т = 245 с.
335
К задаче 11.15 |
|
К задаче 11.16 |
|
Задача 11.16. Определить время выравнивания уровней в двух |
|||
резервуарах при начальном напоре Н0 |
= 4 м. Диаметры резервуа- |
||
ров D1 = 1,6 м и D2 = 3,2 м, h0 = 1,5 |
м. Перетекание происходит |
||
через цилиндрический насадок диаметром d = 100 мм, коэффици- |
|||
ент расхода которого μ = 0,82. |
|
|
|
Ответ. Т = 7,9 мин. |
|
|
|
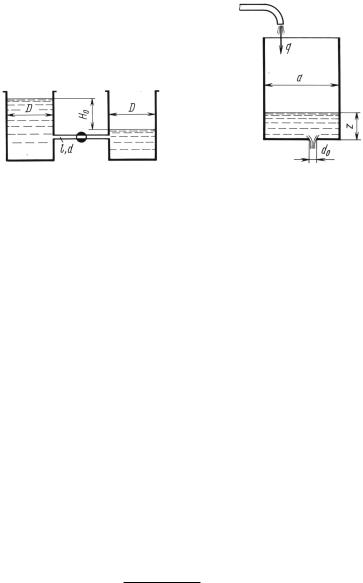
Задача 11.17. Два одинаковых резервуара диаметром D = 0,8 м, |
|||
заполненные маслом (ν = 1,4 Ст) с начальной разностью уровней |
|||
Н0 = 1,2 м, соединены трубкой диаметром d = 12 мм и длиной |
|||
l = 6 м. |
|
|
|
Найти время, необходимое для того, чтобы разность уровней |
|||
уменьшилась до H = 0,1 м, |
учитывая в трубке только потери тре- |
||
ния.Указание. Предварительно выяснить режим течения в трубке (см. |
|||
гл. 9). |
|
|
|
Ответ. Т = 29,2 ч. |
|
|
|
Задача 11.18. В первоначально пустой бак квадратного сечения |
|||
(a = 800 мм) подается постоянный расход воды q = 2 л/с. Одновре- |
|||
менно поступающая вода вытекает через донное отверстие диаме- |
|||
тром d0 = 30 мм (коэффициент расхода отверстия μ = 0,6). |
устано- |
||
1. Каков предельный уровень zmax, соответствующий |
|||
вившейся работе системы? |
|
чтобы разность между zmax |
|
2. Какое время требуется для того, |
|||
и текущим уровнем z стала |
z = 0,1 м? |
|
|
Ответ. 1. zmax = 1,1 м. 2. t = 25 мин. |
|
||
336 |
|
|
|
К задаче 11.17 |
|
|
|
|
|
|
|
|
|
|
|
|
К задаче 11.18 |
||||
Задача 11.19. Шлюзовая камера заполняется из водохранилища |
|||||||||||||||||
с неизменным уровнем путем подъема ворот на высоту s = 2 м, |
|||||||||||||||||
производимого с постоянной скоростью v = 10 мм/с. |
|||||||||||||||||
1. Определить высоту |
Н1, на которую поднимается уровень во- |
||||||||||||||||
ды в камере за время подъема ворот, а также время полного запол- |
|||||||||||||||||
нения камеры, если длина камеры |
L = 180 м и начальная разность |
||||||||||||||||
уровней Н0 |
= 10 м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. Какова должна быть скорость подъема ворот, чтобы камера |
|||||||||||||||||
заполнилась целиком к моменту их подъема на заданную высоту s? |
|||||||||||||||||
Коэффициент расхода отверстия под нижней кромкой ворот |
|||||||||||||||||
считать постоянным и равным μ = 0,6. |
|
|
|
||||||||||||||
Указание. Для первого этапа заполнения камеры (во время подъема |
|||||||||||||||||
ворот) дифференциальное уравнение процесса имеет вид |
|||||||||||||||||
|
|
|
|
|
−F dz = Qdt, |
|
|
|
|||||||||
где F – площадь камеры (F = BL); z – |
разность уровней в водохранилище |
||||||||||||||||
и камере; Q – расход через отверстие под щитом, Q = μBvt√2gz (здесь |
|||||||||||||||||
В – ширина камеры). |
|
|
|
|
|
|
|
s2√ |
|
2 |
|
||||||
|
|
|
|
|
|
|
2g |
|
|||||||||
Ответ. 1. H1 = H0 − √ |
|
|
− |
μ |
|
|
|
|
= 7,15 м; |
||||||||
H0 |
|
|
|||||||||||||||
|
4Lv |
||||||||||||||||
|
|
v |
|
|
|
|
|
|
|
|
мин |
|
|||||
|
|
μs√2g |
|
|
|
|
|
||||||||||
|
T = |
s |
+ |
2L√H0 |
− |
H1 |
= 5,2 |
|
. |
||||||||
|
|
|
|
||||||||||||||
Задача |
2. v = 4,7 мм/с. |
опускаясь с постоянной скоростью v = |
|||||||||||||||
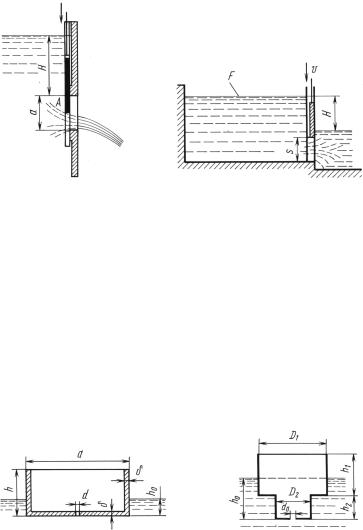
11.20. Щит A, |
|||||||||||||||||
= 0,05 м/с, |
перекрывает квадратное отверстие (а = 1 м) в верти- |
||||||||||||||||
кальной стенке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
337 |

К задаче 11.19
Считая уровень воды в резервуаре постоянным (H = 3 м), опре- |
||
делить, сколько воды вытечет за время закрытия отверстия. Коэф- |
||
фициент расхода отверстия принять в процессе закрытия постоян- |
||
ным и равным μ = 0,59. |
|
|
Указание. Расход через отверстие в момент времени t от начала за- |
||
крытия |
|
|
Q = μa(a − vt)s2g H + |
a + vt |
. |
2 |
||
Ответ. V = 50 м3. |
|
|
|
Задача 11.21. Шлюзовая камера площадью F = 800 м2 имеет |
|||
перепускное прямоугольное отверстие высотой s = 2 м и шириной |
|||
В = 4 м, которое начинает закрываться щитом, движущимся с по- |
|||
стоянной скоростью v = 0,05 |
м/с. |
|
|
Определить понижение у |
уровня в шлюзовой камере за время |
||
закрытия отверстия, истечение через которое происходит под по- |
|||
стоянный уровень. |
|
|
|
Начальный напор Н = 5 м. |
|
||
Коэффициент расхода отверстия принять постоянным и равным |
|||
μ = 0,65. |
|
|
|
Ответ. y = 1,2 м. |
|
|
|
Задача 11.22. |
Квадратный ящик со стороной основания a = 3 м, |
||
высотой h = 1,2 |
м и толщиной стенок δ = 150 мм плавает, погру- |
||
женный в воду на глубину h0 |
= 0,6 |
м. |
|
Определить время затопления ящика с момента открытия дон- |
|||
ного отверстия диаметром d = |
30 мм (коэффициент расхода |
||
μ = 0,82). |
|
|
|
338 |
|
|
|
|
К задаче 11.20 |
|
|
|
|
|
|
К задаче 11.21 |
|
||||||||
Ответ. |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
− |
|
|
|
|
|
|
|
|
|
|||||||
|
μf√2g "√h0 − δ − |
h − δ − (h − h0) F0 # = 57 мин, |
|||||||||||||||
T = F0 0 |
F ∙ |
|
|||||||||||||||
|
F |
F |
2 |
|
|
|
|
|
|
|
|
|
F |
|
|||
где F0 = a2; F = (a − 2δ)2 и f = |
4 . |
|
|
|
|
||||||||||||
Задача 11.23. Определить |
πd2 |
|
|||||||||||||||
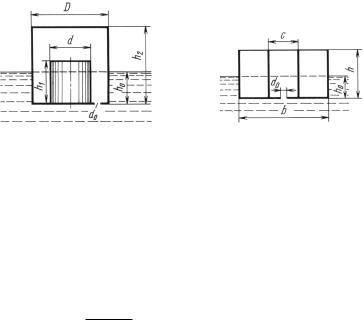
время |
затопления тонкостенного со- |
||||||||||||||||
суда после открытия донного отверстия диаметром d0 |
= 25 мм. Со- |
||||||||||||||||
суд имеет два цилиндрических участка, диаметры которых D1 = |
|||||||||||||||||
= 1,2 м и D2 |
= 0,6 м, |
а высоты h1 = 0,8 м и h2 = 0,5 |
м. Начальное |
||||||||||||||
погружение сосуда h0 |
= 0,85 м. |
|
|
|
|
|
|
|
|||||||||
Коэффициент расхода отверстия μ = 0,6. |
|
||||||||||||||||
|
К задаче 11.22 |
К задаче 11.23 |
|
|
Указание. Затопление сосуда происходит в два этапа: |
|
|
||
1) |
погружение при переменном напоре истечения через отверстие до |
|||
момента времени, когда сосуд заполнится водой на высоту h2; |
+ D12 |
|||
2) |
погружение при постоянном напоре истечения z = h0 −h2 |
|||
до момента полного затопления сосуда. |
|
|
h2D22 |
|
|
339 |
|||
|
|
|
||
Ответ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
D12 |
|
D22 |
|
|
|
2 |
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
D22 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
T |
|
|
t |
|
|
t |
|
|
|
|
|
|
|
h |
0 − s |
h |
|
|
h |
|
h |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
" |
|
− |
|
2 D12 # + |
|||||||||||||||
|
= |
|
1 + 2 = D12 − D22 d02 μ√2g |
|
|
|
0 |
|
2 + |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
h1 + h2 − h0 − h2 |
|
2 |
|
|
|
|
= 9 мин. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
D2 |
D2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
+ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
d |
|
μs2g h0 − h2 + h2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
0 |
|
D2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
D12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Задача 11.24. Открытый цилиндрический сосуд (диаметром |
||||||||||||||||||||||||||||||||||
D = 1, 5 |
м и высотой h2 |
= 1,6 |
м), |
внутри которого свободно поме- |
||||||||||||||||||||||||||||||
щается круглый деревянный брус, плавает в воде, погруженный на |
||||||||||||||||||||||||||||||||||
глубину h0 |
= 0,6 |
м. Диаметр бруса d = 0,8 м, его высота h1 = 0,8 м |
||||||||||||||||||||||||||||||||
и относительная плотность δ = 0,75. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
К задаче 11.24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
К задаче 11.25 |
|
|
|
|||||||||
Определить время затопления сосуда с момента открытия дон- |
|||||||||||||||||||||||||||||
ного отверстия диаметром d0 = 30 мм, коэффициент расхода кото- |
|||||||||||||||||||||||||||||
рого μ = 0,62. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Толщиной стенок сосуда пренебречь. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Указание. Затопление сосуда будет происходить при переменном на- |
|||||||||||||||||||||||||||||
поре истечения через отверстие до момента всплытия бруса, а затем – при |
|||||||||||||||||||||||||||||
постоянном напоре истечения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ответ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− s |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
μ√2 |
|
|
|
|
− |
|
|
2 |
|
|||||||
|
|
|
|
|
|
2 |
|
|
2 |
D2 |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
||||
T = t1 + t2 = |
D |
d−2 |
d |
|
|
|
|
|
2 |
√h0 |
|
|
h0 |
|
δh1 |
|
|
+ |
|||||||||||
|
|
|
d2 |
|
|
|
g |
|
|
D |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
D2 |
|
h2 − h0 − δh1 1 − |
|
|
|
= 22, 4 |
мин |
|
|
|
|
|
|
|
||||||||||||||
+ |
D2 |
. |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
d02 |
|
μv2g h0 |
|
δh1 |
|
d |
|
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
− |
D ! |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
340 |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
