
- •Содержание
- •1. Введение.
- •1.1 Общие закономерности химических процессов. Классификация процессов общей химико-технологических процессов
- •Требования к химическим производствам
- •Компоненты химического производства
- •Разделение на две твердые фазы:
- •Разделение жидкости и твердого вещества:
- •1.2 Промышленный катализ
- •Основные положения теории катализа.
- •1.3. Сырьевая база химической промышленности.
- •Классификация сырья
- •Характеристика минерального сырья
- •Химическое сырье
- •Растительное и животное сырье
- •Характеристика разработок минерального сырья
- •Качество сырья и методы его обработки
- •Способы сортировки:
- •Способы обогащения:
- •Сырьевая база химических производств
- •1.4 Энергетическая база химических производств
- •1.5 Критерии оценки эффективности производства
- •1.5.1. Интегральные уравнения баланса материальных потоков в технологических процессах. Понятие о расходных коэффициентах. Относительный выход продукта
- •1.5.2. Балансы производства
- •1. Материальный баланс
- •2. Энергетический (тепловой) баланс
- •3. Экономический баланс
- •1.5.3. Технологические параметры химико-технологических процессов.
- •1.6.Принципы создания ресурсосберегающих технологий
- •2. Теоретические основы химической технологии
- •2.1. Энергия в химическом производстве. Тепловой эффект реакции в технологических расчетах. Направленность реакции в технологических расчетах
- •2.2 Массообменные процессы. Основные принципы массообменных процессов. Моделирование процессов теплообмена.
- •Молекулярная диффузия. Первый закон Фика
- •Турбулентная диффузия
- •Уравнение массоотдачи
- •Уравнение массопередачи
- •Связь коэффициента массопередачи и коэффициентов массоотдачи (или уравнение аддитивности фазовых сопротивлений)
- •Подобие массобменных процессов
- •3. Химическое производство как сложная система. Иерархическая организация процессов в химическом производстве
- •3.1. Химико-технологические системы (хтс). Элементы хтс. Структура и описание хтс. Методология исследования хтс, синтез и анализ хтс.
- •Методология исследование химико-технологических систем.
- •3.2. Сырьевая и энергетическая подсистема хтс
- •1. Классификация химических реакторов по гидродинамической обстановке.
- •2. Классификация химических реакторов по условиям теплообмена.
- •3. Классификация химических реакторов по фазовому составу реакционной массы.
- •4. Классификация по способу организации процесса.
- •5. Классификация по характеру изменения параметров процесса во времени.
- •6. Классификация по конструктивным характеристикам.
- •3.4. Промышленные химические реакторы. Реакторы для гомогенных процессов, гетерогенных процессов с твердой фазой, гетерогенно-каталитических процессов, гетерофазных процессов.
- •Реакторы для гетерогенных процессов с твердой фазой.
- •Реакторы для гетерогенно-каталитических процессов.
- •4. Основные математические модели процессов в химических реакторах
- •4.1. Идеальные химические реакторы. Непрерывный реактор идеального вытеснения. Непрерывный реактор идеального смешения
- •4.2. Сравнение эффективности проточных реакторов идеального смешения и идеального вытеснения. Обоснование использования каскада реакторов.
- •Каскад реакторов смешения.
- •Влияние степени конверсии.
- •Влияние температуры.
- •5. Применение кинетических моделей для выбора и оптимизации условий проведения процессов
- •5.1. Экономические критерии оптимизации и их применение для оптимизации реакционных узлов.
- •Оптимальные концентрации инициатора и температуры в радикально-цепных реакциях
- •Оптимизация степени конверсии.
- •7. Важнейшие промышленные химические производства
- •7.1 Проблема фиксации атмосферного азота. Синтез аммиака, Физико-химические основы производства и обоснование выбора параметров и типа реакционного узла. Технологическая схема процесса.
- •Синтез аммиака
- •Сырье для синтеза аммиака.
- •Технология процесса.
- •Основные направления в развитии производства аммиака.
- •7.2. Получение азотной кислоты. Физико-химические основы химических стадий процесса, обоснование выбора параметров и типа реакторов. Технологическая схема процесса.
- •Физико-химические основы процесса.
- •Контактное окисление аммиака.
- •Обоснование роли параметров и их выбор.
- •Окисление оксида азота (II) до диоксида.
- •Абсорбция диоксида азота.
- •Технология процесса.
- •7.3. Производство минеральных удобрений. Классификация минеральных удобрений
- •Классификация минеральных удобрений.
- •7.3.1. Азотные удобрения. Физико-химические основы производства нитрата аммония. Устройство реакционного узла. Теоретические основы процесса и его технологическое оформление
- •Производство нитрата аммония.
- •7.3.2. Производство фосфорной кислоты. Физико-химические основы процесса. Технологическая схема
- •Функциональная схема производства эфк.
- •Сернокислотное разложение апатита.
- •7.3.3. Фосфорные удобрения. Физико-химические основы процессов их производства. Типы реакционных узлов.
- •Производство простого суперфосфата.
- •Производство двойного суперфосфата
- •Азотнокислое разложение фосфатов. Получение сложных удобрений
- •Обжиг серосодержащего сырья.
- •Обоснование роли параметров и их выбор.
- •Сжигание серы.
- •Окисление диоксида серы.
- •Обоснование роли параметров и их выбор.
- •Технология контактного окисления so2.
- •Абсорбция триоксида серы.
- •Перспективы развития сернокислотных производств.
- •7.5. Электрохимические производства. Теоретические основы электролиза водных растворов и расплавленных сред. Технология электролиза раствора хлорида натрия.
- •Основные направления применения электрохимических производств
- •Электролиз раствора хлорида натрия
- •Электролиз раствора NaCl с твердым катодом и фильтрующей диафрагмой
- •Электролиз раствора хлорида натрия с ртутным катодом
- •7.6. Промышленный органический синтез
- •Первичная переработка нефти.
- •Каталитический риформинг углеводородов.
- •7.6.2. Производство этилбензола и диэтилбензола. Теоретические основы процесса и обоснование выбора условий процесса. Технология процесса
- •7.6.3. Синтезы на основе оксида углерода. Производство метанола. Теоретические основы процесса.
- •Окисление изопропилбензола (кумола)
- •Технологическая схема получения фенола и ацетона кумольным способом.
- •7.6.5. Биохимические производства. Особенности процессов биотехнологии.
- •7.6.5.1. Производство уксусной кислоты микробиологическим синтезом
- •7.6.5.2. Производство пищевых белков
- •8. Химико-технологические методы защиты окружающей среды
- •8.1. Утилизация и обезвреживание твердых отходов
- •8.2. Утилизация и обезвреживание жидких отходов
- •8.3. Обезвреживание газообразных отходов
4. Основные математические модели процессов в химических реакторах
4.1. Идеальные химические реакторы. Непрерывный реактор идеального вытеснения. Непрерывный реактор идеального смешения
Эффективность любого химического процесса, выражаемая показателями производительности и селективности, в значительной степени определяется кинетической моделью процесса. В свою очередь характер этой модели определяет тип реактора, при котором достигается наиболее высокое значение указанных показателей. Наиболее удобно выявит влияние типа реактора на тот или иной процесс и его показатели на примере идеальных реакторов.
Классификация химических реакторов, основанная на структуре потока реакционной массы, различает идеальный реактор периодического действия, непрерывный реактор идеального вытеснения и непрерывный реактор идеального смешения.
Идеальный периодический реактор может
быть представлен как емкостной аппарат,
снабженный мешалкой, число оборотов
которой обеспечивает равенство
концентраций компонентов реакции в
любой точке объема,
![]() и постоянство температуры по объему
(
и постоянство температуры по объему
(![]() ).
).
Дополнительное условие идеальности такого реактора состоит в одновременной и моментальной загрузке всех компонентов исходной смеси.
Скорость протекания реакции
![]() в таком реакторе во времени определяется
выражением
в таком реакторе во времени определяется
выражением
![]() (1)
(1)
Для периодических реакторов реакционный объем обычно постоянен и тогда уравнение (1) приобретает простой вид
![]() (2)
(2)
Из последнего выражения следует, что
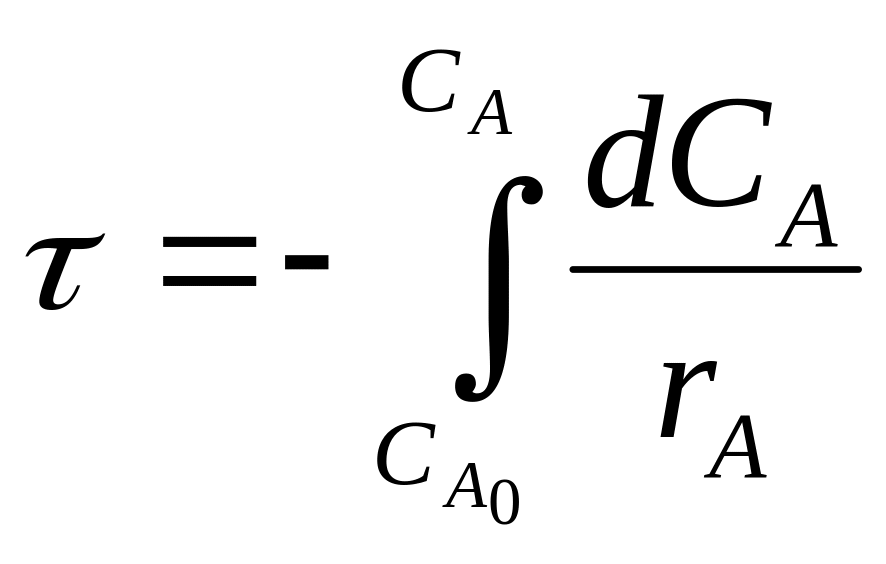 (3)
(3)
Так как
![]() ,
где ХА – степень превращения
компонента А, то
,
где ХА – степень превращения
компонента А, то
![]()
Уравнение (3) переходит в вид
![]() (4)
(4)
Уравнение (4) является основой для расчета
реакторов периодического действия. Оно
справедливо для любого компонента
простой и сложной реакции, причем для
нахождения интеграла надо подставить
в него функцию
![]() .
.
В непрерывном реакторе идеального вытеснения реакционная масса движется вдоль оси потока, вытесняя последующие слои. Условие идеальности такого аппарата состоит в том, что каждый элемент реакционной массы в данном поперечном сечении движется вдоль оси потока с одинаковой скоростью
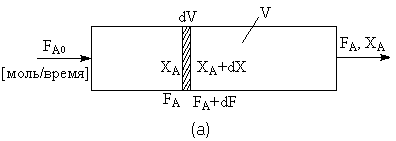
В этой модели исключается торможение потока насадкой или стенками и диффузионные явления, из которых особенно существенно обратное или продольное перемешивание потока. При стационарном режиме работы, т.е. при постоянных во времени скорости, составе поступающей смеси и температуре, каждый элемент реакционной массы пребывает в реакторе идеального вытеснения одинаковое время, а концентрации реагентов и температура в каждом поперечном сечении остаются постоянными. В этом случае концентрации меняются только по длине аппарата, что позволяет составить дифференциальное уравнение материального баланса для элементарного объема dV в единицу времени
![]()
Интегрирование этого уравнения по всему
реакционному объему V,
когда количество вещества меняется от
![]() до FA
дает:
до FA
дает:
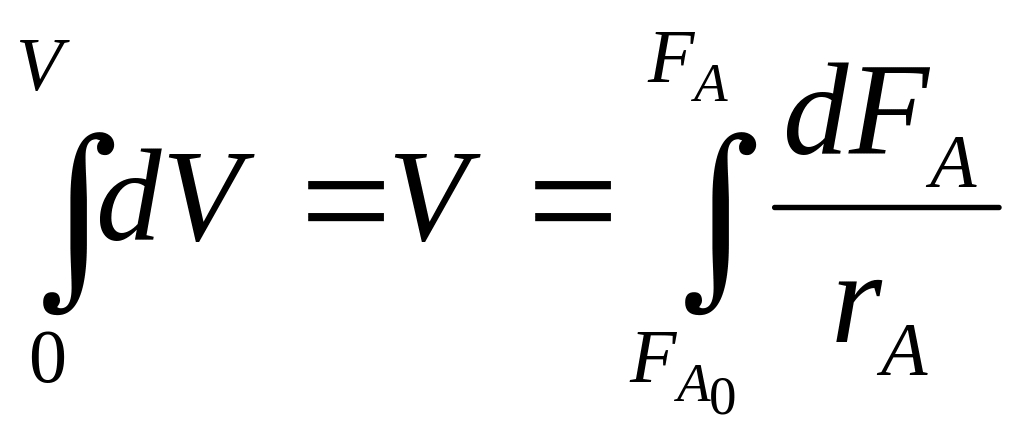 (5)
(5)
Так как
![]() ,
то это уравнение можно привести к виду
,
то это уравнение можно привести к виду
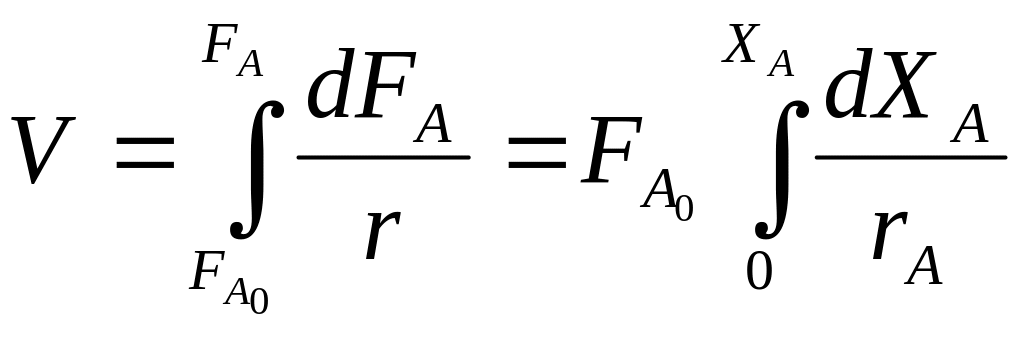 (6)
(6)
или
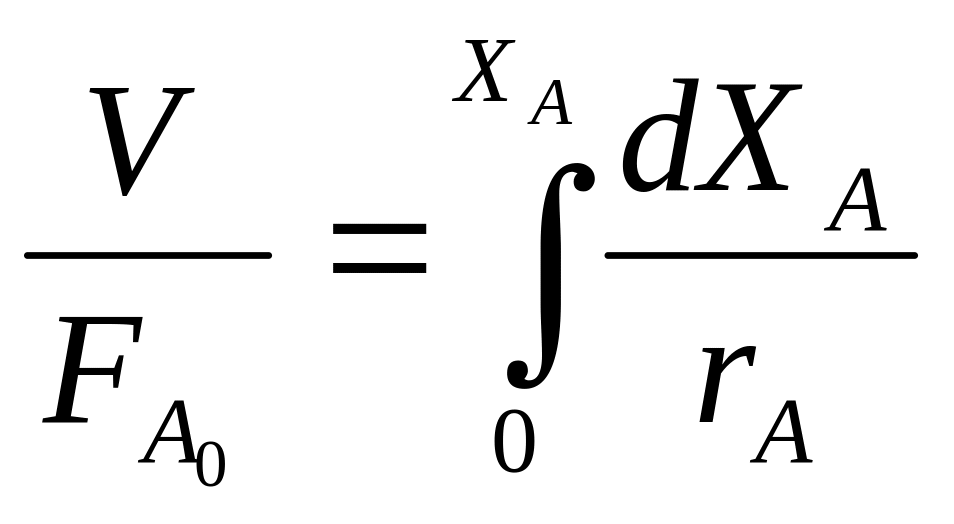 (7)
(7)
Обратная величина левой части последнего
уравнения
![]() представляет собой удельную нагрузку
реактора по реагенту А (число молей
этого реагента в единицу времени на
единицу реакционного объема).
представляет собой удельную нагрузку
реактора по реагенту А (число молей
этого реагента в единицу времени на
единицу реакционного объема).
Умножая обе части уравнения (7) на
![]() ,
получаем
,
получаем
 (8)
(8)
Сравнение полученного уравнения с
уравнением (4) для периодического
идеального реактора показывает полную
идентичность их правой части. В то же
время выражение для левой части уравнения
также имеет размерность времени, при
этом величина
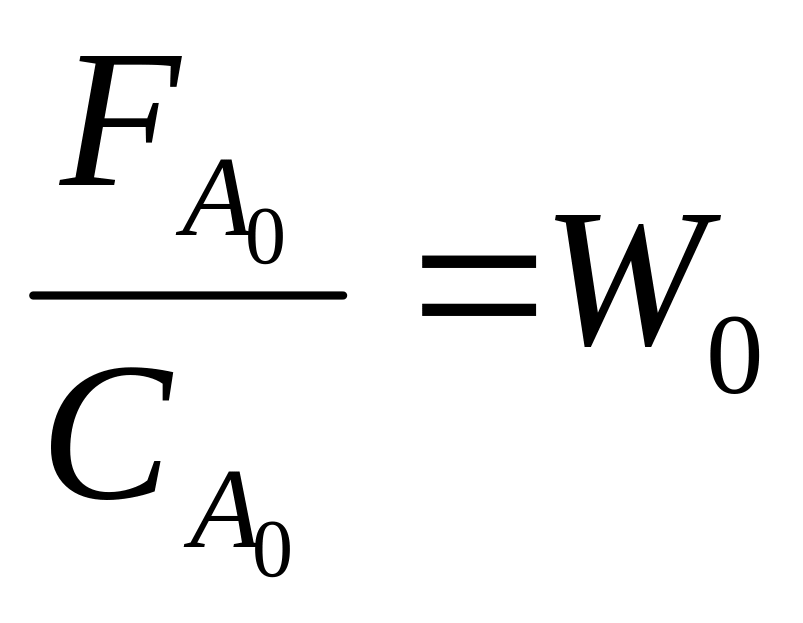 представляет собой объемную скорость
реакционного потока на входе в реактор.
Тогда левая часть представляет собой
время контакта
представляет собой объемную скорость
реакционного потока на входе в реактор.
Тогда левая часть представляет собой
время контакта
![]()
В этом случае уравнение (8) приобретает вид
![]() (9)
(9)
полностью идентичный уравнению (4) для
периодического идеального реактора. В
общем случае величину контакта
![]() называют условным временем.
называют условным временем.
