
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
11.7 ] Вынужденное рассеяние Мандельштама–Бриллюэна (ВРМБ) 691
Схема на рис. 11.8 представляет собой генератор излучения на комбинационной частоте и может быть названа комбинаци-
онным лазером. Между зеркалами ре- |
|
|
|
|
|
|
|
|
|
|
зонатора (полностью отражающего , M1 |
|
|
|
M2 |
|
|
|
|||
1 |
|
1 2 |
|
|
|
|
|
|||
и частично прозрачного 2) помещает- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ся кристалл рубина 1, являющийся ис- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||
точником импульса на частоте , сосуд |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
с нелинейной средой (бензолом) 2 и ячей- |
|
Рис. 11.8 |
|
|
|
|
|
|
||
ка Керра 3, служащая для получения ги- |
|
|
|
|
|
|
|
|
|
|
гантских импульсов излучения (напряженности 107–108 В/см). В комбинационное излучение преобразуется до 20 % энергии импульса на основной частоте .
11.7. Вынужденное рассеяние Мандельштама– Бриллюэна (ВРМБ)
В 1964 г. был экспериментально обнаружен эффект, предсказанный ранее советским физиком Л.И. Мандельштамом (1879– 1944) и французским физиком Л. Бриллюэном (1889–1969): мощное лазерное излучение частоты , попадая на кристалл, индуцирует в нем появление упругой (акустической) волны частоты с одновременным рассеянием света на частоте .
Качественное объяснение этого эффекта с классической точки зрения таково. Из-за сильной связи атомов друг с другом в твердых телах и жидкостях тепловое колебательное движение одного атома неизбежно передается другому. Такое движение можно рассматривать как совокупность упругих (акустических) волн, распространяющихся во всевозможных направлениях и имеющих всевозможные частоты, спектр которых чрезвычайно широк: от звуковых ( 102 Гц) до гиперзвуковых ( 1010 Гц). Акустические волны в среде — это волны плотности (или давления), появление которых влияет и на оптические свойства среды: изменения плотности, с «оптической» точки зрения, это изменения числа осцилляторов в единице объема что, согласно классической теории дисперсии, приводит к изменениям (флуктуациям) показателя преломления Æ , , имеющих волновой характер.
Итак, тепловое движение приводит к появлению в среде волн показателя преломления, которые можно представить в виде совокупности бегущих плоских волн различных частот и направлений K. Любая из волн в этой совокупности может быть записана в виде
Æ , Æ0 # , |
(11.33) |
где волновое число есть, по определению, зв ( зв — скорость звука в среде), т. е. каждая волна показателя преломления

692 |
Элементы нелинейной оптики |
[ Гл. 11 |
Æ , представляет собой бегущую фазовую синусоидальную решетку; — начальная фаза.
Что же происходит, когда световая волна большой интенсивности -0 , 0 ! падает на среду, состоящую из набора таких бегущих решеток? Чтобы в этом разобраться, вернемся к проблемам, которые мы обсуждали, рассматривая процесс записи и восстановления объемных голограмм (голограмм Денисюка).
Прежде всего заметим, что бегущую интерференционную картину : , в объемной среде можно создавать с помощью интерференции опорной волны -0 , с «предметной» волной
-1 , $ 1 ! # |
(11.34) |
Cуммарная картина интенсивности
: , -0 , -1 , 2
(где черта означает усреднение за время, существенно большее периода светового колебания и много меньшее периода «биений» 2$ ) имеет вид
2 |
2 |
2 0 1 # |
(11.35) |
: , 0 |
1 |
Напомним, что можно, находя сумму гармоничных колебаний с близкими частотами, воспользоваться векторной диаграммой: интенсивность суммарного колебания (квадрат длины суммарного вектора) найти с помощью теоремы косинусов.
Обратите внимание, что последнее слагаемое в (11.35) описывается точно таким же соотношением, что и (11.33). Ясно поэтому, что если фотообработку полученной голограммы осуществить таким образом, чтобы голограмма стала «фазовой», т. е. чтобы оптическая плотность (т. е. показатель преломления) объемной среды после обработки стала пропорциональна интенсивности суммарной волны при записи голограммы, то наша голограмма при восстановлении изображения ничем не будет отличаться от среды, в которой возбуждена бегущая решетка (11.33). Разумеется, мы говорим сейчас о некоторой гипотетической голограмме с изменяющейся во времени функцией пропускания. Мы знаем, что голограмма в процессе восстановления изображения, при освещении ее волной, совпадающей с опорной волной, которая была использована при записи, восстанавливает предметную волну.
Ясно поэтому, что волна -0 , , дифрагируя на бегущей фазовой решетке вида (11.35), дает «рассеянную» волну, которая отличается от (11.34) лишь встречным направлением (встречным перемещением волновых фронтов). Поскольку фазовая решетка, созданная тепловыми флуктуациями, чрезвычайно слаба
11.8 ] |
Обращение волнового фронта |
693 |
Æ0 0 , то и дифрагировавшая волна имеет чрезвычайно малую амплитуду, если амплитуда волны -0 , не достаточно велика.
Поскольку акустические волны (11.33) разных частот и направлений имеют случайную начальную фазу (они созданы тепловым движением, имеющим случайный характер), то
и рассеянные разными решетками волны некогерентны — это так называемое спонтанное рассеяние, аналогично излучению
обычных тепловых источников, которое образовано спонтанным, несогласованным излучением разных атомов.
Чрезвычайно важно, далее, обратное воздействие на среду электрического поля волны -0 , большой интенсивности, которая способна влиять на оптические свойства среды (изменять ее показатель преломления). Интерферируя с первоначально слабой, дифрагировавшей на «тепловой» решетке волной -1 , , эта волна создает в среде бегущую решетку, которая ничем не отличается от уже имеющейся в среде решетки (которая и «породила» волну -1 , ). Дополнительное давление в среде и, следовательно, дополнительное изменение ее показателя преломления пропорционально квадрату напряженности суммарного поля -2 -0 -1 2 — нелинейный эффект, который мы уже обсуждали, рассматривая явление самофокусировки и самоканализации. Таким образом, «затравочная», первоначально слабая волна показателя преломления когерентно усиливается бегущими волнами, образованными интерференцией интенсивной волны -0 и рассеянной волны -1. Последняя, благодаря увеличению амплитуды Æ0 волны показателя преломления, также когерентно усиливается (ведь она возникает в результате дифракции на фазовой решетке со все большей глубиной модуляции фазы Æ0 0). Таким образом, как амплитуда акустической волны, так и амплитуда рассеянной волны частоты будут постепенно нарастать по мере распространения в нелинейной среде — их энергия черпается из исходной волны -0 , — волны накачки. В отличие от некогерентного рассеяния на тепловых флуктуациях показателя преломления, вынужденное мощной волной накачки рассеянное излучение является когерентным.
11.8. Обращение волнового фронта
Смысл термина волна с «обращенным» волновым фронтом состоит в том, что в обращенной волне волновые поверхности (поверхности одинаковой фазы колебаний), имея ту же пространственную форму, перемещаются во встречном направлении, т. е. в каждой точке волнового фронта волновой вектор k имеет противоположное направление. Можно сказать, что обращенная
694 |
Элементы нелинейной оптики |
[ Гл. 11 |
волна повторяет ход прямой волны, но в обратной последовательности — «обращает ход событий во времени».
Математически это выражается в том, что комплексная амплитуда обращенной волны 7обр , в каждой точке , , связана с комплексной амплитудой прямой волны 7 равенством 7обр 7 . Например, для плоской волны с комплекс-
ной амплитудой D ' (# — начальная фаза), обращенной является волна D ' , что подразумевает изменение знака всех трех компонент вектора k, а также изменение знака начальной фазы #. Расходящаяся сферическая волна 0 D ' после обращения становится сходящейся волной 0 D ' .
Вспомним, что волне с комплексной амплитудой 7
D соответствует реальный волновой процесс - ,
, т. е. обращение волнового фронта означает, что реальная волна - , превращается в волну -обр ,
. Тот же самый результат получается, если |
|||||||||
в реальном волновом процессе изменить знак времени (заме- |
|||||||||
нить на ). Мы получим - , , что |
|||||||||
(в силу четности функции #) равно - , |
|||||||||
, а это и есть обращенная волна. Поэтому-то обращенная |
|||||||||
волна воспроизводит все изменения, которые происходят с пря- |
|||||||||
мой волной по мере ее распространения (быть может, в неодно- |
|||||||||
родной среде), но в обратном порядке. |
|
|
|
||||||
|
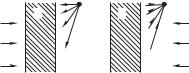
Рисунок 11.9 напоминает нам схему записи и восстановле- |
||||||||
ния объемной голограммы (запись во встречных пучках). Рису- |
|||||||||
нок 11.9 а — схема записи: слева на голограмму падает опорная |
|||||||||
(в нашем случае плоская) волна 1, справа — предметная волна. |
|||||||||
В нашем случае предмет — точечный источник света, и соответ- |
|||||||||
ственно, предметная волна — это «сферическая» волна, расходя- |
|||||||||
щаяся из источника — точки 9. Направление штрихов условно |
|||||||||
показывает положение слоев интерференционных максимумов и |
|||||||||
минимумов, которые после фотообработки образовали объемную |
|||||||||
|
|
|
|
|
|
фазовую |
решетку |
(т. е. чере- |
|
1 |
2 |
S |
2 |
S |
|
дующиеся |
слои |
б´ольшего |
и |
|
|
|
|
|
1 |
меньшего |
показателя прелом- |
||
|
|
|
|
|
ления в объемной регистри- |
||||
|
|
|
|
|
|
||||
|
3 |
|
|
3 |
|
рующей среде 2). |
|
|
|
|
|
|
|
|
|
Рисунок 11.9 б — схема вос- |
|||
|
à |
|
á |
|
|
становления изображения. Вос- |
|||
|
|
Рис. 11.9 |
|
|
станавливающая волна 1 пада- |
||||
|
|
|
|
|
|
ет на голограмму |
справа, т. е. |
||
навстречу опорной волне 1 при записи голограммы. Дифрагируя |
|||||||||
на объемной фазовой решетке 2 эта волна образует восстанов- |
|||||||||
ленную волну 3 — сферическую волну, сходящуюся в точку 9 . |
|||||||||
11.8 ] Обращение волнового фронта 695
Эта сходящаяся сферическая волна имеет «обращенный» по отношению к расходящейся предметной волне волновой фронт.
Рисунок 11.10 иллюстрирует замечательное свойство обращенной волны. Пусть на слой неоднородной среды направлен параллельный пучок света 1 (с плоским волновым фронтом). То-
гда на выходе из слоя волновые поверхности 3 окажутся сильно |
||||||
искаженными, деформированны- |
|
|
|
|
|
|
ми (рис. 11.10 а). Если нам за- |
1 |
2 |
3 |
1 |
2 |
3 |
тем удалось обратить волновой |
|
|
||||
|
|
|
|
|
|
|
фронт с помощью некоего «вол- |
|
|
|
|
|
|
шебного зеркала» и заставить |
|
|
|
|
|
|
обращенную волну 3 пройти тот |
|
|
|
|
|
|
же слой неоднородной среды 2 |
|
à |
|
|
|
á |
в обратном направлении, то на |
|
|
|
Рис. 11.10 |
|
|
выходе из слоя мы получим хо- |
|
|
|
|
|
|
роший параллельный пучок света 1 — ту же форму волнового фронта, который имела волна до того, как ее волновой фронт был «испорчен» (рис. 11.10 б).
Голография, как мы видели, дает возможность получить обращенную волну в двухэтапном процессе (сначала этап записи голограммы, а затем стадия реконструкции — восстановления изображения, восстановления обращенной волны).
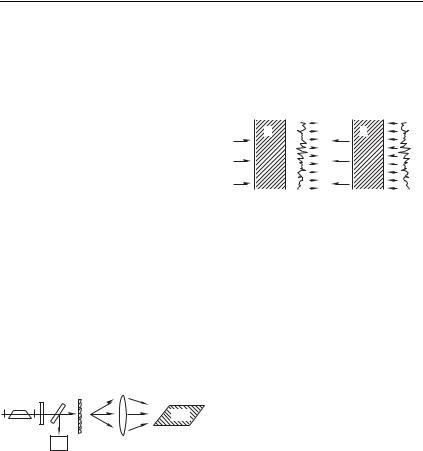
При вынужденном комбинационном рассеянии обращенная волна возникает в реальном времени, непосредственно при освещении нелинейной среды волной большой интенсивности. Схема
D |
|
эксперимента, |
подтверждаю- |
|
щего, что при ВРМБ возни- |
||
|
|
||
|
ÍÑ |
кает обращенная волна, пока- |
|
Ê Ï |
Ë |
зана на рис. 11.11. Лазерный |
|
пучок большой |
интенсивно- |
||
Рис. 11.11 |
сти, имеющий хороший волно- |
|
вой фронт, искажается затем |
||
|
матовой пластинкой П, которая сильно деформирует форму волнового фронта. Затем с помощью линзы Л, которая в основном перехватывает весь рассеянный пластинкой свет, излучение направляется на нелинейную среду НС (кювета, заполненная метаном или сероуглеродом). После обратного рассеяния (ВРМБ) свет вновь проходит через линзу и матовую пластинку. При этом искажения, которые были внесены в пучок при его распространении слева направо, компенсируются при обратном ходе волны через ту же искажающую среду, и на выходе из пластинки П слева от нее волновой фронт снова становится «хорошим», почти плоским, что и контролируется с помощью полупрозрачного зеркала E, отводящего часть отраженного обратно излучения в систему контроля . Понятно, что такая компенсация внесенных в пучок искажений возможна лишь по-
696 |
Элементы нелинейной оптики |
[ Гл. 11 |
тому, что рассеянное назад нелинейной средой излучение точно воспроизводит форму сложного волнового фронта падающей на среду волны, лишь изменяя направление перемещения волновых фронтов на противоположное. Кювета с нелинейной средой и является тем «волшебным зеркалом», которое обращает ход событий во времени. (Если бы вы вдруг решили, что то же самое можно сделать, установив вместо кюветы с нелинейной средой самое обыкновенное зеркало, то вы убедились бы, что при обратном ходе волны через матовую пластинку искажения не скомпенсировались бы, а лишь увеличились, добавившись к уже имевшимся искажениям: обыкновенное зеркало не превращает расходящуюся сферическую волну в сходящуюся — расходящаяся волна отразившись от зеркала, остается расходящейся.)
Предметный указатель
Абсолютно неупругий удар, 116 |
Волна холостая, 685 |
|
— твердое тело, 126 |
— электромагнитная, 509, 512 |
|
— упругий удар, 115 |
— — в ионосфере, 649 |
|
Автогенератор Ван-дер-Поля, 466 |
— — в металлах, 649 |
|
Автоколебания, 464 |
— — , отражение от идеального провод- |
|
Амплитуда волны, 477 |
ника, 522 |
|
— колебания, 385 |
— — , поляризация, 513 |
|
— — комплексная, 483 |
— — , энергетические характеристики, |
|
Амплитудная модуляция, 396 |
514 |
|
— решетка, 567 |
— эллиптически поляризованная, 485 |
|
Анизотропная среда, 653 |
Волноводы, 524 |
|
Атом Томсона, 418, 424 |
Волновое поле, 563 |
|
Атомная поляризуемость, 645 |
— число, 477 |
|
Биения, 398, 399 |
Волновой вектор, 478 |
|
— пакет, 640 |
||
Бинормаль, 33 |
||
— параметр, 564 |
||
Брюстера угол, 360 |
||
Волновые поверхности, 477 |
||
Вектор, 22 |
||
Волны в анизотропных средах, 653 |
||
— , модуль, 23 |
— — кристаллах, 655 |
|
— Пойнтинга, 353, 514, 516, 661, 662, |
— — нелинейных средах, 672, 676 |
|
684 |
— — плазме, 377 |
|
— Умова, 494 |
— — среде, 351 |
|
— плотности потока энергии, 494 |
— , генерация третьей гармоники, 680, |
|
— поля скоростей, 34 |
682 |
|
— угловой скорости, 33 |
— квазимонохроматические, 535, 544 |
|
Векторное произведение, 33 |
— , параметрическая генерация, 686 |
|
Вес, 44, 108, 109 |
— электромагнитные, 361, 508 |
|
Видность, 531, 547, 553–556, 558, 559 |
— — на границе двух сред, 353, 357, 359 |
|
Волна, 474, 476 |
— — , поляризация, 359 |
|
— бегущая плоская, 479 |
— , эффект возникновения комбинацион- |
|
— в анизотропных средах, 653 |
ных частот, 685 |
|
— векторная, 484 |
||
— , — удвоения частоты, 673, 676 |
||
— гармоническая, 477 |
||
Время корреляции, 538, 551 |
||
— линейно-поляризованная, 484, 485, |
||
— постоянная, 428 |
||
513, 514 |
||
— регистрации, 539 |
||
— монохроматическая, 482 |
||
Вынужденное рассеяние Мандель- |
||
— накачки, 685 |
||
штама–Бриллюэна, 691 |
||
— необыкновенная, 656, 659, 661 |
||
Вязкость, 157 |
||
— обыкновенная, 656, 659 |
||
— , коэффициент, 158 |
||
— плоская, 476, 477 |
||
Газовый разряд, 366 |
||
— плоскополяризованная, 484, 513, 519 |
||
— поляризации, 685 |
— — дуговой, 371 |
|
— поляризованная по кругу, 485 |
— — искровой, 371 |
|
— поперечная, 484, 501 |
— — коронный, 371 |
|
— предметная, 624 |
— — несамостоятельный, 370 |
|
— продольная, 484 |
— — самостоятельный, 370 |
|
— сигнальная, 685 |
— — тлеющий, 370 |
|
— , скорость в волноводе, 526 |
Гармоники боковые, 402 |
|
— стоячая, 479, 496, 501 |
Гармонический осциллятор, 419 |
|
— — , пучности, 480, 517 |
— — , колебания вынужденные, 438 |
|
— — , узлы, 479, 517 |
— — , — затухающие, 425 |
|
— — электромагнитная, 517 |
— — , — свободные, 420 |
|
— сферическая, 480, 481 |
— — , уравнение, 419 |
|
— ударная, 504 |
Гиромагнитное отношение, 259 |
|
— упругая, 487 |
Гироскоп, 136, 137 |
|
— — в жидкостях и газах, 490 |
Гистерезис, 223, 268 |
|
— — в стержне, 497 |
Главные оси инерции, 137 |
