студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

Уравнение движения осциллятора имеет в этом случае вид

*3 -0

Мы по-прежнему полагаем, что затухание отсутствует, а поле световой волны меняется по гармоническому закону с частотой .

Переходя, как и ранее, к уравнению для поляризации 6!D, получаем

где 63 60 — малая поправка к решению 60 линейного уравнения (11.5), которое, как мы знаем, описывается функцией (11.6). Подставляя решение (11.17) в уравнение (11.16)

(поскольку остальные слагаемые малы в сравнении с 603), получим для нелинейной поправки 63 линейное дифференциальное уравнение

Точно такой же вид имеет уравнение линейного осциллятора, вынужденные колебания которого возбуждаются внешней силой,

меняющейся со временем пропорционально 3 .

Поскольку 3 3 3 4, то правая часть (11.18) — «внешняя сила» — представляется суммой двух сил, одна из которых меняется с частотой , а вторая — с утроенной частотой 3 . Соответственно, и вынужденные колебания 63 также являются суммой гармонических колебаний с частотами и 3 . Найдя решение, отвечающее каждому из двух слагаемых правой части (11.18), получим в результате полное выражение для поляризации среды 6 ,

11.3 ] Генерация третьей гармоники 683

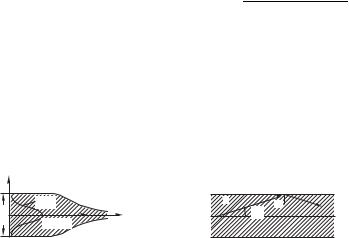
тового пучка становится подобной собирающей линзе. Диаметр пучка по мере распространения в среде постепенно уменьшается

так, как если бы на его пути находилась фокусирующая линза. Этот нелинейный эффект называется самофокусировкой.

Разумеется, фокусирующему воздействию нелинейной среды препятствует дифракционная расходимость пучка: в обычной (линейной) среде с показателем преломления пучок сечения с плоским волновым фронтом не может распространяться, оставаясь параллельным пучком неизменного сечения. Угловая расходимость пучка, определяемая дифракцией, рав-

на 0 0 , где 0 — длина волны в вакууме. Смысл последнего равенства состоит в следующем: пучок

света ограниченного сечения может быть представлен суммой плоских волн разных направлений, причем в этой сумме заметную амплитуду имеют лишь плоские волны, направления которых (углы с осью ) ограничены углом 0. Если для волны, распространяющейся под углом 0, выполнено условие полного внутреннего отражения на границе пучка и окружающей среды:

#пред 0 (рис. 11.6), то и для всех волн, направления которых '0, это условие также будет выполнено, т. е. дифракци-

онная расходимость пучка оказывается полностью скомпенсированной фокусирующим эффектом полного отражения. Получаем

для угла дифракционной расходимости 0 0 0 0 , на-

Последняя формула определяет пороговое значение напряженности поля в световой волне, при которой пучок распространяется в нелинейной среде без расходимости (т. е. дифракционная расходимость компенсируется полным внутренним отраже-

нием) и сечение пучка остается неизменным. Этот нелинейный эффект называется самоканализацией.

Свяжем напряженность поля -0 с мощностью пучка, т. е. с потоком энергии, проходящим через сечение пучка в единицу времени. Мы имеем 9 <0 2- — абсолютная величина век-

684 Элементы нелинейной оптики [ Гл. 11

тора Пойнтинга и, поскольку - , то 9 <0 -2

Например, пороговая мощность излучения рубинового лазера ( 694,3 нм) в сероуглероде равна приблизительно 6пор20 кВт.

11.4. Параметрические процессы в нелинейных средах

Пусть в среде с квадратичной нелинейностью (11.3) распространяются две монохроматические волны с частотами 1 и

2: -1 -1 1 и -2 -2 2 . Повторяя выкладки проведенные в гл. 11.2, вновь придем к уравнению (11.9), опре-

деляющему поправку 61 к линейному приближению 60 . Последнее в нашем случае является решением уравнения

Решение этого (линейного) уравнения является, очевидно, суммой двух решений, каждое из которых отвечает «своей» правой части

60 <0H1-1 1 <0H2-2 2 ,

где H1 и H2 — диэлектрические восприимчивости на частотах 1

Наличие в правой части слагаемых, содержащих квадраты полей -1 , и -2 приводит к уже рассмотренным нами эффектам: генерации вторых гармоник с частотами 2 1 и 2 2 и оптическому выпрямлению (появлению постоянного электрического поля).

Новый эффект, который здесь возникает, связан с наличием в правой части слагаемого, содержащего произведение

1 2 , что эквивалентно сумме двух колебаний с частотами 1 2 и 1 2. Соответственно нелинейная поправка к поляризации 61 содержит колебания на частотах 1 2

11.4 ] Параметрические процессы в нелинейных средах 685

и 1 2, что приводит к переизлучению на этих частотах, причем амплитуды волн пропорциональны произведению -1-2 амплитуд исходных волн с частотами 1 и 2. Генерация волн с суммарной и разностной частотой позволяет получать когерентное излучение в более широком диапазоне частот. Кроме того, появляется возможность, смешав в нелинейном кристалле инфракрасное излучение (ИК) с видимым светом, преобразовать частоту ИК-диапазона в видимый спектр, где шумовые характеристики существующих приемников света существенно лучше

приемников ИК-области спектра.

Качественно эффект возникновения комбинационных частот в излучении, прошедшем нелинейную среду, можно понять следующим образом. Пусть волна частоты 1 имеет достаточно большую амплитуду, так что ее распространение в среде приводит к изменению оптических свойств среды с частотой 1, т. е. под действием этой волны возникает модуляция показателя преломления среды, а следовательно, модуляция фазы второй волны. Мы знаем, что спектр колебания, имеющего несущую частоту 2, фаза которого промодулирована с частотой 1, содержит компоненты с боковыми частотами 1 2.

Пусть в среде распространяются волны с частотами 1 и2 и пусть волна частоты 1 имеет большую амплитуду, приводящую к нелинейному изменению свойств среды (возникно-

вению квадратичной нелинейности в кристалле). Назовем мощную волну -1 частоты 1 волной накачки, а слабую волну -2 частоты 2 сигнальной волной. Это приводит, как мы видели,

к появлению нелинейной добавки 61 к поляризации среды 60 , которая осциллирует с частотой 1 2 3. Колебания поляризации с частотой 3 индуцируют в среде вторичные волны — переизлучение на этой частоте. Волна поляриза- ции 61 , 1 3 !1 !2 распространяется в среде с фазовой скоростью ф 3 , где ! !1 !2. Направим теперь на нелинейный кристалл, в котором распространяются волны с частотами 1 и 2, третью волну малой интенсивности, частота которой равна 1 2 3. Эту волну называют холостой. Выберем направление холостой волны (волновой вектор !3) так, чтобы выполнялось условие !3 !1 !2. Тогда ее уравнение имеет вид

-3 , 3 3 !3 ,

а ее фазовая скорость ф 3 3 совпадает с фазовой скоростью волны поляризации.

686 Элементы нелинейной оптики [ Гл. 11

Переизлученные волной поляризации 61 , вторичные вол-

Амплитуда колебаний волны поляризации пропорциональна амплитуде волны накачки (частоты 1), поэтому и вторичные волны частоты 3 также пропорциональны ее амплитуде. В результате исходная слабая волна -3, благодаря фазовому синхронизму со вторичными волнами той же частоты, усиливается по

мере прохождения в нелинейной среде, черпая свою энергию из исходной сильной волны — явление называется параметрическим усилением света.

Поместим нелинейный кристалл, например, кристалл ниобата лития LiNbO3 (KDP) между зеркалами 1 и 2 оптического резонатора (рис. 11.7). Кристалл сориенти-

торых 2 и 3 удовлетворяют условию резонанса, выполнялось условие фазового синхронизма (11.25). Волна накачки -1 от внешнего лазера попадает на кристалл через зеркало 1, прозрачного для волны -1. Слабое излучение -2 и -3 (с частотами2 и 3) существует в резонаторе благодаря колебаниям осцилляторов, возбужденных тепловым движением. Для волн -2 и -3, частоты которых удовлетворяют условию 2 3 1, а волновые векторы — условию фазового синхронизма !2 !3 !1, возникает усиление первоначально слабого спонтанного излучения на частотах 2 и 3. Если при достаточно мощной волне накачки усиление превосходит потери за проход (включая потери при отражении от зеркал, поглощение и рассеяние), происходит самовозбуждение генератора. Изменение ориентации кристалла приводит к тому, что условие фазового синхронизма выполняется для другой пары частот 2 и 3, так как благодаря изменению показателя преломления необыкновенной волны, распространяющейся вдоль оси резонатора, изменяются волновые числа. Таким образом, может осуществляться плавная перестройка частоты генерации. Генерация волн с частотами 2 и 3 происходит бла-

годаря модуляции параметров нелинейной среды под действием поля волны накачки, что и обусловливает название — параметрическая генерация.

В связи со сказанным выше имеет смысл вспомнить о параметрической раскачке механических или электрических колебаний (см. гл. 3).

11.5.Комбинационное рассеяние света

Влинейном приближении квазиупругая сила, действующая на оптический электрон со стороны поля ядра, может быть представлена как производная от потенциальной энергии

,2 2: 7 ., . .

Если смещение электрона не мало, то в выражении для потенциальной энергии следует учитывать следующий член разложения в степенной ряд по потенциальной энергии:

откуда получается квадратичная поправка к квазиупругой силе

7 # 2

При этом следует учесть, что потенциальная энергия в положении равновесия 0 принимается равной нулю и, кроме того, линейный по член в выражении , отсутствует, поскольку положение равновесия соответствует минимуму потенциальной энергии, т. е. ., . 0 0.

Изучая поведение оптических электронов в поле световой волны, мы полагали, что из-за большой массы ядра атомов не смещаются. Рассмотрим теперь эффекты, возникающие при учете этого смещения. Пусть смещение ядра относительно узла кристаллической решетки, где оно находится в отсутствие поля, либо относительно положения равновесия в молекуле жидкости или газа есть . При учете этого смещения потенциальная энергия (как функция двух переменных и ) может быть записана

ввиде

,, #22 82 2 13 3 13 +3 *2 #2 (11.27)

Используя это выражение, получаем силу, действующую на электрон. Она имеет вид

Эффект, связанный с появлением квадратичной поправки по мы уже обсуждали. Он отличен от нуля лишь в анизотропной среде и приводит к генерации второй гармоники. Здесь мы его учитывать не будем. Последнее слагаемое зависит только от закона колебания ядра , которое из-за большой массы имеет низкие частоты, далеко выходящие за рамки оптического диапазона (соответствующее излучение осцилляторов приходится на далекую инфракрасную область). Это слагаемое мы также рассматривать не будем.

В результате остаются два слагаемых

7 2*,

причем второе (нелинейное) слагаемое является малой поправкой к квазиупругой силе .

Используя полученное выражение, имеем уравнение движения электрона

2* D-0

Вводя эквивалентную жесткость квазиупругой силы

где зависящая от движения ядра собственная частота осциллятора равна

Переходя от уравнения для к уравнению для поляризации 6 D!, получаем

Обратимся теперь к уравнению, описывающему колебания ядра массы . Упругую силу, действующую на ядро, найдем, дифференцируя выражение для энергии (11.27) по координате :

+2 2# *2

Априори ясно, что смещение ядра мало, поэтому членом можно пренебречь. Третье слагаемое не существенно, так как произведение меняется с частотой, близкой к частоте колебаний электрона, которая велика по сравнению с частотой колебаний тяжелого ядра (другими словами, за время, равное периоду колебаний ядра, это слагаемое в силе множество раз изменяет знак, поэтому его усредненное влияние ничтожно). Остаются лишь два слагаемых:

электрона на колебания ядра существенно лишь в случае сильного поля, когда необходимо учитывать нелинейное слагаемое. В слабых полях (обычных тепловых источников света) им можно также пренебречь. В этом случае уравнение движения ядра имеет вид

D-0

Наконец, влиянием поля световой волны высокой частоты пренебрежем (так же, как мы пренебрегли быстро меняющимся

690 Элементы нелинейной оптики [ Гл. 11

где 6 !D — поляризация, обусловленная смещением оптического электрона.

Пусть теперь источником возбуждения является сильное световое поле (мощный импульс излучения лазера), а нелинейная среда, в которой возникает комбинационное излучение, помещена в резонатор. Две причины заставляют нас учесть теперь влияние этого слагаемого.

Учтя ранее влияние колебания ядра на колебание электрона, мы выяснили, что поляризация среды состоит из слагаемых на частотах и . Учтем далее лишь стоксову компоненту, т. е. будем полагать

6 6 # 6 #

Ясно, что при этом 62 содержит слагаемое, осциллирующее на разностной частоте . Эта частота совпадает с резонансной частотой колебаний молекулы и может вызвать сильную раскачку этих колебаний. Разумеется, воздействие на этой частоте имело место и при тепловом возбуждении, однако комбинационное излучение, возбужденное тепловым движением, имеет случайную фазу, т. е. фазы колебаний разных молекул не согласованы между собой, поэтому и не возникает эффективного накопления излучения на комбинационной частоте. При помещении нелинейной среды в резонатор, комбинационное излучение, которое распространяется вдоль оси резонатора, отражается от зеркал и, следовательно, вновь возвращается в нелинейную среду, оказывая обратное влияние на колебания молекул: их фазы колебаний оказываются согласованными, а комбинационное из-

лучение когерентно. Такое комбинационное излучение называется вынужденным или стимулированным.

Ситуация отличается от предыдущей в двух отношениях. Во-первых, увеличивается амплитуда колебаний внешнего воздействия на молекулу на резонансной частоте (она пропорциональна амплитуде колебаний поляризации на частоте и, следовательно, амплитуде колебания светового поля в импульсе излучения лазера).

Во-вторых, комбинационное излучение, распространяющееся вдоль оси резонатора, отражаясь от зеркал, накапливается в резонаторе и «синхронизирует» колебания молекул: их комбинационное излучение оказывается когерентным (при когерентном сложении интенсивность пропорциональна !2, в отличие от некогерентного, при котором интенсивность пропорциональна !).