
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
10.6 ] |
Вопросы и задачи |
671 |
3.Некогерентная смесь линейно-поляризованного света и света, поляризованного по кругу, рассматривается через поляроид. Найдено положение поляроида, соответствующее максимальной интенсивности прошедшего света. При повороте поляроида из этого положения на угол 30Æ интенсивность света уменьшилось на 20 %. Найти отношение интенсивности света + , поляризованного по кругу, к интенсивности линейно поляризованного света.
4.Как будет окрашена в скрещенных поляроидах кристаллическая пла-
стинка, дающая разность хода 0 650 нм. Ответ: в синий свет (дополнительный к оранжевому).
5.Один поляроид пропускает 30 % света, если на него падает естественный свет. После прохождения света через два таких поляроида интенсивность падает до 9 %. Найти угол между разрешенными направ-
лениями поляроидов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Плоская монохроматическая волна, поляризован- |
|
|
|
1 |
|||
|
|
||||||
ная по кругу, создает в точке 6 интенсивность |
+0. На |
|
|
|
|
||
|
|
|
|
P |
|||
пути волны ставят две большие пластинки 1 и 2 |
в 4, |
|
|
|
|
|
|
|
|
|
|
|
|||
как показано на рис. 10.15. Главные направления пла- |
|
|
|
2 |
|||
|
|
||||||
|
|
|
|
|
|
||
стинок ориентированны взаимноперпендикулярно. Най- |
|
||||||
|
|
|
|||||
ти интенсивность + в точке 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. Расположив пластинку из исландского шпата, вы- |
Рис. 10.15 |
||||||
резанную параллельно его оптической оси, между скре- |
|||||||
щенными поляроидами, можно осуществить монохроматор, позволяющий задержать одну из спектральных линий дублета натрия и
пропустить другую. Какой должна быть минимальная толщина пластинки и как ее следует ориентировать? Показатели преломления и $ для исландского шпата
1 1,48654, $1 1,65846 (для линии 1 589 нм),2 1,48652, $2 1,65843 (для линии 2 589,6 нм).
8.Показатель преломления кристаллического кварца для длины волны
589 нм равен $ 1,544 для обыкновенной волны и 1,553 для необыкновенной волны. На пластинку из кварца, вырезанную параллельно оптической оси, нормально падает линейно-поляризованный свет, занимающий спектральный интервал 40 нм. Найти толщину пластинки и направление поляризации падающего света, если свет на выходе из пластики оказался неполяризованным.
Г л а в а 11
ЭЛЕМЕНТЫ НЕЛИНЕЙНОЙ ОПТИКИ
11.1.Модель нелинейной среды
Вявлениях, которые мы изучали до сих пор (интерференция
идифракция, дисперсия и распространение волн в анизотропных средах), молчаливо предполагалось, что характеристики среды, в которой распространяются волны (в частности ее показатель преломления < ), не зависят от того, велика или мала напряженность электрического поля волны (хотя, конечно, показатель преломления может зависеть от координат, если среда неоднородна и от ориентации вектора E, если она неизотропна). Следствием является линейность волнового уравнения и справедливость принципа суперпозиции: распространение волны в среде не изменяет ее свойства, поэтому одна волна проходит в среде так, как будто другой волны нет — волны распространяются в среде, не «замечая» друг друга.
Независимость показателя преломления от напряженности поля для световых волн, излучаемых обычными тепловыми источниками (нить накаливания электрической лампы, нагретый газ и т. д.), обусловлена пренебрежимой малостью поля световых волн по сравнению с внутренним микроскопическим полем в веществе. Напряженность поля в излучении обычных источ-
ников не превосходит величины порядка 104 В/м. Сравните эту величину например, с полем, действующим на электрон в атоме водорода: D 4$<0 2 1,5 1011 В/м.
Можно ожидать, что световая волна изменит характеристики среды, если ее поле окажется сравнимо с внутриатомными полями в веществе. Возможность получения интенсивных пучков света появилась после создания квантовых генераторов советскими физиками А.М. Прохоровым (1916–2002) и Н.Г. Басовым (1922–2001) и независимо от них американским физиком Ч.Х. Таунсом (р. 1915) в 1954 г. В сфокусированном лазерном пучке напряженность поля достигает значений порядка 108–1010 В/м. Именно лазеры открыли по-настоящему эру нелинейной оптики (хотя и до их создания отдельные нелинейные эффекты в оптике наблюдались).
Чтобы понять механизм влияния интенсивных световых волн на свойства среды, полезно вернуться к модели, которую мы использовали ранее: материальная среда представляет собой набор
11.2 ] |
Эффект удвоения частоты. Оптическое выпрямление |
673 |
осцилляторов (не взаимодействующих между собой в простейшем случае). Осциллятор — это оптический электрон в атоме. Исследуя ранее явление дисперсии, мы молчаливо предполагали, что напряженность поля световой волны достаточно мала, поэтому малым оказывается смещение электрона из положения равновесия, вызванное этим полем. При малых смещениях r, сила, действующая на электрон со стороны поля ядра и стремящаяся вернуть электрон в положение равновесия, предполагалась пропорциональной смещению (квазиупругая сила):
, |
(11.1) |
подобно тому, как малые деформации пружины при ее растяжении или сжатии приводят к линейной зависимости упругой силы от величины деформации — закон Гука. Исходя из линейной связи (11.1) мы и получали ранее линейную связь между поляризацией среды и напряженностью поля световой волны <0H , где H — поляризуемость среды — определяется формулой (9.11)
ине зависит от E.
Всильных полях смещение уже нельзя считать малым, при этом связь между силой и смещением усложняется: в линейное соотношение (11.1) следует ввести нелинейные поправки. Для того чтобы понять, какова их роль и к каким эффектам они приводят, будем далее полагать что поправки, возникающие в сильных полях, являются все же малыми по сравнению с первым (линейным) слагаемым.
2 / 3, |
(11.2) |
здесь и / — константы, и именно они, как мы увидим далее, приводят к новым оптическим эффектам.
В общем случае в анизотропной среде направление смещения r не совпадает с направлением «упругой силы», возвращающей электрон в положение равновесия, однако мы далее будем пользоваться упрощенной моделью, считая, что векторы f и r параллельны (т. е. в равенстве (11.2) 2 и / 3 /2 ).
11.2. Эффект удвоения частоты. Оптическое выпрямление
Рассмотрим вначале эффекты, к которым приводит наличие лишь первой нелинейной поправки, т. е.
2 |
(11.3) |
Отметим, что такого рода зависимость невозможна в изотропных средах или в кристаллах, обладающих центром симметрии, например, в кубических кристаллах, поскольку, согласно (11.3),
22 Основы физики. Т. I


676 |
|
Элементы нелинейной оптики |
|
|
[ Гл. 11 |
||||||
убедиться, имеет вид |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
62 |
|
'*0 |
2 2 |
|
(11.10) |
||||
|
|
|
2 |
|
|
||||||
|
|
|
0 2 |
|
|
|
|
|
|
||
Итак, к колебанию поляризации среды 60 <0H0- , |
|||||||||||
изменяющейся с частотой возбуждающей волны - , прибавля- |
|||||||||||
ются два слагаемых: одно из них — постоянная (не меняющаяся |
|||||||||||
во времени) добавка к поляризации |
6 *-2 |
2 |
|
||||||||
|
|
|
0 0 и второе слага- |
||||||||
емое — колебание поляризации 62 , происходящее с удвоенной |
|||||||||||
частотой. Итак: |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6 <0H0-0 |
'*0 |
|
'*0 |
|
2 |
(11.11) |
|||||
2 |
2 |
4 |
2 |
||||||||
|
|
|
|
0 |
|
0 |
|
|
|
|
|
Согласно (11.11) колебание гармонического светового поля |
|||||||||||
- возбуждает в среде колебание поляризации, которое не |
|||||||||||
является гармоническим. Спектр функции 6 содержит кро- |
|||||||||||
ме компоненты частоты (совпадающей с частотой колебаний |
|||||||||||
световой волны) также и спектральную компоненту удвоенной |
|||||||||||
частоты, а также постоянную составляющую. Мы хорошо знаем, |
|||||||||||
что в линейных системах внешнее гармоническое воздействие |
|||||||||||
приводит к возникновению вынужденных колебаний, частота |
|||||||||||
которых совпадает с частотой внешней силы. Присутствие двух |
|||||||||||
последних слагаемых в (11.11) свидетельствует о возникновении |
|||||||||||
двух нелинейных эффектов. |
|
|
|
|
|
|
|
|
|||
Постоянная добавка к поляризации среды ответственна за |
|||||||||||
появление в среде постоянных, не меняющихся во времени по- |
|||||||||||
ляризационных зарядов. Эти поляризационные заряды создают |
|||||||||||
свое собственное постоянное, не меняющееся во времени, элек- |
|||||||||||
трическое поле. Итак, в нелинейной среде быстропеременное |
|||||||||||
поле световой волны (меняющееся со световой частотой ) по- |
|||||||||||
рождает постоянное не меняющееся во времени поле. По понят- |
|||||||||||
ным причинам этот нелинейный эффект называют оптическим |
|||||||||||
выпрямлением. |
|
|
|
|
|
|
|
|
|
|
|
Последнее |
слагаемое в |
|
(11.11) |
— |
колебание поляризации |
||||||
с удвоенной частотой. Это колебание приводит к переизлучению |
|||||||||||
на частоте 2 . Таким образом, монохроматическая световая вол- |
|||||||||||
на частоты приводит к возникновению в среде переизлученной |
|||||||||||
|
|
3 |
|
|
|
волны |
|
удвоенной |
частоты. |
||
1 |
2 |
|
|
|
Волна |
|
удвоенной |
частоты |
|||
|
|
|
|
|
|||||||
|
|
|
|
|
|
существует, конечно, наряду |
|||||
Ë1 |
|
|
|
|
|
с переизлучением на часто- |
|||||
|
|
|
|
|
те , обусловленным пер- |
||||||
Рис. 11.1 |
|
|
|
вым слагаемым в поляриза- |
|||||||
|
|
|
ции 6 . |
|
|
||||||
|
|
|
|
|
|
|
|
||||
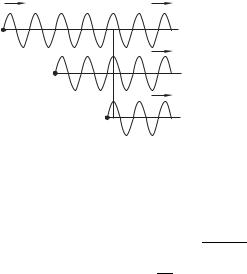
Схема одного из первых экспериментов, демонстрирующая |
|||||||||||
эффект удвоения частоты, показана на рис. 11.1. |
|
||||||||||

11.2 ] Эффект удвоения частоты. Оптическое выпрямление 677
Импульс излучения рубинового лазера 1 ( 1 694,3 нм) фокусировался с помощью объектива Л1 в кристалле кварца 2. Мощность в импульсе длительности 10 мкс составляла приблизительно 10 кВт. Излучение, выходящее из кристалла, содержит, кроме переизлучения с длиной волны 1, также и вторую гармонику ( 2 347,15 нм), лежащую в ультрафиолетовой области спектра. Оно анализируется с помощью призменного спектрографа 3.
В первых экспериментах (1961 г.) мощность, преобразованная во вторую гармонику, составляла приблизительно 0,1 мВт, т. е. около 10 8 мощности исходного лазерного импульса.
Чтобы понять, почему в первых экспериментах коэффициент преобразования энергии исходной волны в волну второй гармоники оказался столь малым, а также понять, каким образом можно его увеличить, рассмотрим более детально волновые процессы, происходящие в нелинейном кристалле.
Итак, пусть исходная волна, бегущая в кристалле, имеет вид
- , -0 1
Это плоская волна частоты , волновое число 1 этой волны определяет ее фазовую скорость
|
|
|
7 |
, |
|
|
|||
1 |
|
|
||
— показатель преломления для волны, имеющей частоту . Эта волна возбуждает в каждой точке среды колебания поляризации с частотой 2 , определяемые формулой (11.10). Существенно, что волна поляризации 62 , бежит с той же фазовой скоростью, что и исходная волна - , . Действительно, если принять, что колебания поля (при любом фиксированном ) происходят по закону -0 , то колебания 62 происходят по закону (11.10), т. е. без сдвига фазы, который зависел бы от .
Ясно поэтому, что волна поляризации 62 , имеет вид
62 , 2 2 1 ,
т. е. волновое число этой волны есть 2 1, а ее фазовая скорость2 2 1 1 как раз оказывается равной фазовой скорости исходной волны. Эту волну поляризации можно рассматривать как бегущую в среде антенну или движущийся и колеблющийся с частотой 2 электрический диполь. Как следствие (см. раздел «Электричество и магнетизм»), должна излучиться волна второй гармоники -2 , частоты 2
-2 , 2 2
Из-за дисперсии ее фазовая скорость 2 2 2 2 не равна, вообще говоря, фазовой скорости исходной волны (так
678 |
Элементы нелинейной оптики |
[ Гл. 11 |
как 2 ), а значит, и фазовой скорости волны поляризации 62 , , т. е. скорости излучающей эту волну антенны. Это означает, что между волнами, излучаемыми «антенной» в разные моменты времени (и в разных местах) возникает фазовый
сдвиг, равный 2 2 1 .
Пока путь волны в кристалле достаточно мал:
2 2 1 $, |
(11.12) |
все «вторичные волны», излученные бегущей антенной, складываются синфазно, поэтому амплитуда суммарной волны нарастает.
v |
Такое |
синфазное |
сложение |
|||
|
схематически |
показано |
на |
|||
1 |
рис. 11.2: |
все три волны, из- |
||||
A |
лученные |
бегущей |
антенной |
|
||
|
в положении 1, 2, 3 оказываются |
|||||
2 |
почти синфазными, |
и |
энергия |
|||
A |
исходной |
волны |
преобразуется |
|||
|
в энергию второй гармоники. |
|
||||
3 |
Условие (11.12), при кото- |
|||||
A |
ром волны второй гармоники, ис- |
|||||
|
пущенные разными осциллятора- |
|||||
Рис. 11.2 |
ми среды, складываясь синфазно, |
|
образуют в сумме волну, амплитуда которой при распространении в кристалле нарастает, называется условием фазового синхронизма. Эффективное расстояние, на котором энергия второй
гармоники нарастает, называется длиной когерентности. Мы |
||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
ког 2 2 1 , |
(11.13) |
где 1 |
, |
2 |
2 2 . Для |
кварца разность пока- |
|
7 |
|
7 |
|
зателей преломления 2 0,025 (для длины волны
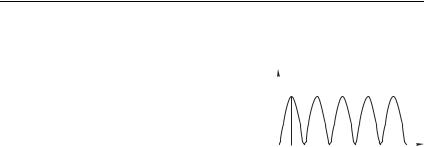
2$ 694,3 нм). Согласно (11.13) длина когерентности оказывается черезвычайно малой: ког 10 10 2 мм. При увеличении пути в кристалле & ког расфазировка вторичных волн, излученных бегущей антенной (волной поляризации 62 , ) становится существенной: амплитуда суммарной волны на частоте 2 начинает уменьшаться, а значит, происходит обратная «перекачка» энергии второй гармоники в исходную волну. Таким образом, по мере распространения в кристалле, волна второй гармоники периодически (с периодом 2 ког) то нарастает, то уменьшается. Качественно зависимость интенсивности второй гармоники от глубины проникновения в кристалл показана на рис. 11.3. Проблема, следовательно, состоит в том, чтобы увеличить длину когерентности и таким образом увеличить размер области, в которой амплитуда второй гармоники нарастает.
11.2 ] Эффект удвоения частоты. Оптическое выпрямление 679
Заметим, что в изотропной среде условие (11.12) невозможно выполнить на всем пути распространения волны в кристалле: из-за дисперсии ( 2 ) оно рано или поздно нарушается. Однако если волна распространя-
ется в анизотропном кристалле, мож- |
|
I |
|
|
|||
|
|
|
|
но, при определенном направлении |
|
|
|
распространения относительно оптиче- |
|
|
|
ский оси, добиться выполнения усло- |
|
|
|
вия 8 . 2 — равенства по- |
|
z |
|
казателей преломления обыкновенной |
|
|
|
O lêîã |
|||
волны частоты и необыкновенной |
|
Рис. 11.3 |
|
волны частоты 2 . |
|
|
|
Напомним, что в линейных средах (т. е. в слабых полях) векторная связь H , справедливая для изотропных сред, заменяется тензорной связью в анизотропной среде:
6 H -
(каждый из индексов , " пробегает значения 1, 2, 3, соответствующие проекциям на оси , , ).
Соответственно, если речь идет о нелинейной среде, то вме-
сто связи
H - ,
справедливой для изотропной среды, в анизотропных кристаллах имеет место равенство:
6 |
H - - - |
(11.14) |
|
, |
|
Будем считать для определенности, что индекс 1 соответствует оптической оси , а индексы 2 и 3 — двум другим главным направлениям и .
Если исходная волна в кристалле является обыкновенной, вектор E в этой волне перпендикулярен оптической оси (проекции - и - равны нулю при ", 1), но благодаря нелинейным слагаемым в (11.14), содержащим произведения - - (т. е. ве-
личины -2-3, -22 и -32), проекция вектора поляризации P на
оптическую ось (ось 1) оказывается отличной от нуля: 6 2# |
|||
|
|
|
1 |
содержит |
слагаемые, пропорциональные величинам - # |
# , |
|
|
|
2 |
-3 |
# # |
и - # |
# . Другими словами, благодаря нелинейности |
|
-2 -2 |
3 |
-3 |
|
обыкновенная волна частоты порождает колебания поляриза-
ции, которые происходят с удвоенной частотой вдоль оптической оси (индексы вверху подчеркивают, что колебания -2 и -3 происходят с частотой , а проекции вектора поляризации на оптическую ось 61 — с частотой 2 ). Колебания поляризации
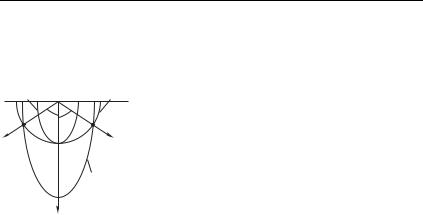
680 |
|
Элементы нелинейной оптики |
[ Гл. 11 |
||||
612# , параллельные оптической оси, порождают световую волну |
|||||||
удвоенной частоты (вторую гармонику), в которой колебания |
|||||||
вектора E также параллельны оптической оси, т. е. вторая гар- |
|||||||
моника |
в кристалле является |
необыкновенной волной. Далее, |
|||||
ve() |
|
vo() |
в некоторых кристаллах можно выбрать |
||||
|
направление распространения, в котором |
||||||
|
|
|
|||||
|
|
|
фазовая скорость необыкновенной волны |
||||
|
|
частоты 2 оказывается равной фазовой |
|||||
|
|
|
скорости обыкновенной волны частоты . |
||||
|
|
|
Рисунок 11.4 иллюстрирует такую воз- |
||||
|
ve(2) |
можность. |
|
|
|
||
|
Например, в отрицательном одноосном |
||||||
|
|
|
|||||
|
|
|
кристалле дигидрофосфата калия KH2PO4 |
||||
Оптическая ось |
(краткое |
название |
KDP), |
имеется |
на- |
||
Рис. 11.4 |
|
правление распространения (целый конус |
|||||
|
направлений), где |
волновая |
поверхность |
||||
|
|
|
|||||
обыкновенной |
волны |
частоты |
(сфера |
8 ) |
пересекается |
||
с волновой поверхностью частоты 2 необыкновенной волны |
|||||||
(эллипсоид . 2 ), т. е. в этом направлении, составляющем |
|||||||
угол с оптической осью (в кристалле KDP 41,5Æ) фазовая |
|||||||
скорость исходной (обыкновенной) волны в кристалле совпадает |
|||||||
со скоростью необыкновенной волны частоты 2 , излучаемой |
|||||||
волной поляризации. Для этого направления условие фазового |
|||||||
синхронизма 2 2 1 выполняется при любом , а это означа- |
|||||||
ет, что на всем пути распространения волны второй гармони- |
|||||||
ки в кристалле ее амплитуда нарастает (происходит перекачка |
|||||||
энергии из исходной волны). Таким образом удается существен- |
|||||||
но увеличить коэффициент преобразования исходной волны во |
|||||||
вторую гармонику. Так, в опытах с кристаллом KDP, в которых |
|||||||
используется лазер на неодимовом стекле ( 1 1,06 мкм — |
|||||||
инфракрасное излучение) во вторую гармонику ( 2 0,53 мкм — |
|||||||
зеленый свет) преобразуется до 30 % энергии исходной волны. |
|||||||
11.3.Генерация третьей гармоники. Самофокусировка
исамоканализация
Рассмотрим теперь эффекты, возникающие благодаря кубической нелинейной поправке в (11.2):
* 3 |
(11.15) |
Такого рода зависимость проявляется в изотропных средах, где квадратичная нелинейность 2 отсутствует (обратим внимание, что изменение знака приводит к изменению знака силы, но не меняет ее абсолютную величину, что характерно для изотропной среды).
