
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
9.3 ] |
Вопросы и задачи |
651 |
Эффектная демонстрация аномальной дисперсии была предложена Кундтом. Использованный им метод скрещенных призм показан на рис. 9.10.
|
Ê |
|
Ê |
|
Ô |
|
Æ |
|
|
|
Ô |
1 |
2 |
1 |
2 |
|
à |
|
á |
|
Рис. 9.10 |
|
|
Первая призма (стеклянная) с вертикальным основанием обладает нормальной дисперсией, поэтому разлагает пучок белого света в горизонтальную радужную полоску: от красного до фиолетового цвета (фиолетовая, более коротковолновая волна, преломляется сильнее).
Вторая (скрещенная) призма имеет горизонтальное основание, поэтому смещает полоску по вертикали. Если она также обладает нормальной дисперсией, то фиолетовая (коротковолновая) часть полоски смещается по вертикали сильнее, чем красная (как показано на рис. 9.10 а).
На рис. 9.10 б вторая призма обладает аномальной дисперсией. В опытах Кундта вторая призма образована пар´ами натрия, обладающими сильным поглощением в желтой части спектра. Именно там, где должна была бы располагаться желтая часть цветной полоски, образуется разрыв (желтая часть спектра поглотилась пар´ами натрия). При этом примыкающая к желтому цвету более длинноволновая часть полоски (для которой & 1) отклоняется вверх (к основанию призмы), а более коротковолновая часть (для нее ' 1) отклоняется вниз, т. е. форма полоски воспроизводит кривую дисперсии .
Вопросы и задачи
1. Вычислить групповую скорость для различных законов дисперсии ( — фазовая скорость):
а) 0 (недиспергирующая среда);
б) (гравитационные волны на поверхности воды);
в) (капиллярные волны); г) (поперечные колебания натянутой струны);
д) 72 )2 2 — электромагнитные волны в ионосфере (7 — скорость света в вакууме, — длина волны в среде).
2. Найти групповую скорость рентгеновского излучения в среде, если предельный угол полного внутреннего отражения при падении этих волн в среду из воздуха равен .

652 |
Дисперсия волн |
[ Гл. 9 |
Ук а з а н и е : закон дисперсии рентгеновских волн определяется выраже- |
||
нием 1 2 2, где — константа. |
|
|
3. Плоская волна |
распространяется в среде с |
законом дисперсии |
), где и ) — постоянные. Показать, что каково бы ни было возмущение, его форма периодически восстанавливается по истечении времени
. 1). Показать, что отношение пути (, пройденного возмущением за время ., к продолжительности этого промежутка, равно групповой скорости.
Ук а з а н и е : достаточно показать, что по истечении времени . восстанавливается взаимное расположение любых двух монохроматических компонент суммарной волны.
4. Показатель преломления ионосферы для радиоволн с частотой @10 МГц равен 0,9. Найти концентрацию B электронов в ионосфере, а также фазовую и групповую скорость для этих радиоволн.
Ответ: B 2,4 1011 м 3.
5. Для оценки интегральных и средних характеристик межзвездной плазмы можно использовать экспериментальный факт, установленный сразу же после открытия пульсаров. Оказалось, что из-за дисперсии плазмы импульсы радиоизлучения пульсаров на более низких частотах всегда запаздывают по отношению к импульсам более высоких частот. Определить полное число свободных электронов на пути сигналов (т. е. их полное число в цилиндре пло-
щадью 1 м2 и высотой, равной расстоянию источник–приемник), если испущенные одновременно импульсы с длинами несущих волн 1 3 см и 2 5 см
запаздывают друг относительно друга на время 10 5 с. Определить также среднюю концентрацию свободных электронов на пути сигналов, если
их относительное запаздывание 0 10 15. Концентрация электронов на пути сигналов не постоянна, хотя показатель преломления мало отличается от единицы.
Ук а з а н и е : воспользуйтесь формулой, связывающей фазовую и групповую скорость волн в плазме: 72; время распространения импульсов определяется групповой скоростью.
|
|
|
|
27 |
|
#0 4 1017, где #0 |
< |
2 |
|
|
2,8 10 13 |
|
|
Ответ: |
|
|
|
|
см, |
||||||||
2 |
2 |
|
7 |
2 |
|
||||||||
B |
|
|
2 1 |
|
|
|
|
|
|||||
2 |
4 10 3 см 3. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
||
|
|
#0 2 1 0 |
|
|
|
|
|
|
|
||||

Г л а в а 10
ВОЛНЫ В АНИЗОТРОПНЫХ СРЕДАХ. ЭЛЕМЕНТЫ КРИСТАЛЛООПТИКИ
10.1. Модель анизотропной среды
Принятая в предыдущей главе модель среды основана на представлении о том, что атомные осцилляторы, заполняющие среду, являются изотропными: ни жесткость квазиупругой связи (и, следовательно, собственная частота осцилляторов), ни коэффициент затухания 5 не зависят от ориентации вектора E в электромагнитной волне, распространяющейся в среде и вызывающей процесс вынужденных колебаний осцилляторов. Согласно (9.9) это означает, что атомная поляризуемость # не зависит от ориентации вектора , а направление дипольного момента атома p совпадает с направлением поля E: # . Не зависят от ориентации E также и диэлектрическая восприимчивость вещества H <0!#, и диэлектрическая проницаемость < 1 H и показатель преломления < . В каком бы направлении не распространялась волна и как бы не был ориентирован вектор E этой волны (в плоскости, перпендикулярной направлению распространения), фазовая скорость волны одна и та же. Суммарное электрическое поле вторичных волн, переизлучаемых колеблющимися осцилляторами, совпадает по направлению с полем первичной волны, поэтому линейно-поляризованная волна (с фиксированной плоскостью колебаний вектора E) остается линейно-поляризованной, и в ней сохраняется неизменной плоскость колебаний суммарного вектора .
В этой главе мы рассмотрим особенности оптических явлений в анизотропных средах. Физическая природа анизотропии
вещества, главным образом монокристаллов, связана с тем, что квазиупругая сила, возвращающая оптический электрон в положение равновесия, обусловлена не только сферически симметричным полем ядра, но и экранирующим полем внутренних оболочек, которые не обязательно 
 сферически симметричны; полем соседних атомов
сферически симметричны; полем соседних атомов
и ионов; а равно и электронов, принадлежащих не конкретному атому, а кристаллу как целому.
На рис. 10.1 показана двумерная механическая модель анизотропного осциллятора. Если внешняя сила, вызывающая процесс малых вы-

654 Волны в анизотропных средах. Элементы кристаллооптики [ Гл. 10
нужденных колебаний, горизонтальна, то квазиупругая сила обусловлена пружинами . При вертикальной внешней силе работают пружины жесткости .
Соответственно различными оказываются и собственные частоты осциллятора при горизонтальных и вертикальных колебаниях о о . Различны, как следует из (9.11), также, поляри-
зуемость # |
# и дипольные моменты 8 8 . |
|||||
|
При |
произвольной |
ориентации |
вектора |
E (с проекциями |
|
- |
и |
- ) |
проекции |
дипольного |
момента |
осциллятора есть |
8 |
# - |
и 8 # - . Ясно, |
что при |
# # вектор p |
||
дипольного момента осциллятора не совпадает по направлению с вектором E.
Итак, в анизотропной среде дипольные моменты осцилляторов не совпадают, вообще говоря, по направлению с электрическим полем волны, которая индуцирует эти дипольные моменты. Соответственно не совпадают по направлению с вектором E и вектор поляризации среды ! и вектор <0 . В отличие от изотропной среды, в которой справедлива векторная связь <0< и свойства которой характеризуются единственным параметром <, в анизотропной среде связь между векторами D и E имеет вид
E <11- <12- <13- <0, |
|
|
E <21- |
<22- <23- <0, |
(10.1) |
E <31- |
<32- <33- <0, |
|
т. е. -компонента вектора D зависит в общем |
случае как от |
|
-компоненты вектора E, так и от его - и -компонент. То же самое касается и других проекций вектора D. Такая связь между векторами D и E называется тензорной, а совокупность девяти
чисел |
|
|
|
|
|
011 |
012 |
013 |
|
< |
021 |
022 |
023 |
|
|
031 |
032 |
033 |
|
образует тензор диэлектрических проницаемостей. Заметим, что тензором называется не любая матрица, но лишь такая, которая связывает два истинных вектора согласно правилу
3
E <0 |
< - |
|
1 |
Компоненты тензора < зависят от выбора системы координат. Можно выбрать направления осей декартовой системы координат так, что симметричный тензор < становится диаго-
нальным: |
|
011 |
0 |
0 |
|
|
|
||||
< |
|
0 |
022 |
0 |
|
|
0 |
0 |
033 |
|

10.2 ] |
Волны в одноосных кристаллах |
655 |
|
В этой системе координат, вместо (10.1), имеем |
|
||
E <0< - , |
E <0< - , |
E <0< - |
(10.2) |
Это означает, что существуют три направления в кристалле, такие, что, если вектор E в волне совпадает с одним из этих направлений, то векторы D и E оказываются коллинеарными. Очевидно, что коллинеарны при этом и векторы E и P: направление дипольного момента атомных осцилляторов совпадает с направлением электрического поля волны. Направления , ,
в кристалле, для которых справедливы равенства (10.2), называются главными направлениями.
Трем параметрам < , < и < соответствуют три главных показателя преломления < , < и < .
Это означает, что волна, в которой вектор E параллелен оси , бежит с фазовой скоростью ; соответственно волны, в которых колебание поля происходит параллельно осям и , имеют фазовые скорости , . Кристаллы, для
которых |
все три главных |
показателя преломления различны: |
|
|
, называются двуосными. Мы далее будем говорить |
||
об одноосных кристаллах, для которых |
. В этом |
||
случае ось называется оптической осью кристалла. |
|||
Показатель преломления обозначают обычно через ., |
|||
показатели преломления |
обозначают |
через 8. Под- |
|
черкнем, что оптическая ось — это не фиксированная прямая в кристалле, а направление, т. е. любая прямая, параллельная
оси , является оптической осью кристалла.
Кристаллы, у которых . & 8 называются положительны-
ми. Примером является кварц, для которого . 8 0,01. У отрицательных кристаллов . ' 8. Примером отрицатель-
ного кристалла является исландский шпат, обладающий сильной анизотропией: 8 . 0,2.
10.2. Волны в одноосных кристаллах
Итак, рассмотрим, как проявляется анизотропия кристалла при распространении в нем световой волны. Пусть , , — главные направления в кристалле, а — оптическая ось.
Прежде всего, введем терминологию, которая используется для описания волновых явлений в одноосных кристаллах.
Плоскость, в которой лежат луч света, т. е. нормаль к волновой поверхности, и оптическая ось, называется главной плоскостью, или главным сечением кристалла. Подчеркнем, что эта
плоскость лишь одной из прямых, ее образующих, привязана к кристаллической структуре, другую же задает световая волна. Если колебания вектора E в волне происходят в главной плос-
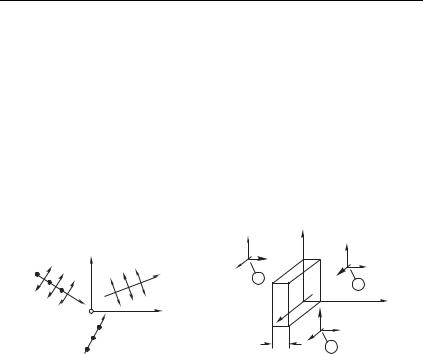
656 Волны в анизотропных средах. Элементы кристаллооптики [ Гл. 10
кости, то такая волна называется необыкновенной (смысл этих терминов будет ясен из дальнейшего).
Пусть, например, луч света 91 лежит в плоскости (плоскость рис. 10.2, где — оптическая ось), тогда плоскость — главная плоскость, а волна 91 — необыкновенная, поскольку колебания E происходят в главной плоскости (что показано поперечными стрелками на рисунке). В волне 92 (луч 92 также лежит в плоскости ) колебания вектора перпендикулярны главной плоскости. Эта волна является обыкновенной. Луч 93 также, как 91 и 92, лежит в плоскости рисунка — плоскости . Эта волна содержит как обыкновенную компоненту (с колебаниями поля, перпендикулярными главной плоскости — плоскости), так и необыкновенную компоненту, в которой колебания поля происходят в плоскости рисунка.
|
|
|
|
Ez |
z |
|
|
|
|
|
|
|
Ez |
|
|
|
z |
|
|
|
|
|
|
|
|
S1 |
k2 |
|
|
Ey |
|
|
|
|
|
|
|||
|
|
|
|
Ex 2 |
k3 |
3 |
|
|
|
|
|
|
y |
||
|
|
|
y |
|
O |
|
|
S3 |
|
|
|
|
|
||
x |
S2 |
|
x |
k1 |
|
|
|
|
|
|
|
Ex |
Ey |
|
|
|
|
|
|
|
|
||
|
|
|
|
d |
1 |
|
|
|
|
|
|
|
|
|
|
Рис. 10.2 |
|
|
Рис. 10.3 |
|
|
||
Рассмотрим вначале, что происходит при распространении света вдоль одного из главных направлений. Пусть монохроматическая волна бежит вдоль оптической оси (волна 1 на рис. 10.3). В поперечной электромагнитной волне, бегущей вдоль оси , вектор E может иметь только - и -проекции - и - , т. е. волну можно рассматривать как суперпозицию двух линейно-по- ляризованных волн, в одной из которых вектор E колеблется вдоль оси , а во второй — вдоль оси . Фазовые скорости этих волн одинаковы: 8. В суммарной
волне вектор E не имеет проекции на оптическую ось (ось ) — она является обыкновенной (ее фазовая скорость определяется
показателем преломления 8). Волна, бегущая вдоль оптической оси — всегда обыкновенная. Распространяясь в кристалле, каждая из составляющих волн - и - приобретает один и тот же фазовый набег 8 , поэтому разность фаз колебаний - и - не меняется по мере распространения волны в глубь кристалла. Это означает, что не изменяется состояние поляризации волны. Если, скажем, на входе в кристалл волна была линейно-поляризована (разность фаз колебаний на входе равна нулю или $, см. § 4.3), то и в любом месте внутри
10.2 ] |
Волны в одноосных кристаллах |
657 |
кристалла она остается линейно-поляризованной с неизменной ориентацией плоскости колебаний вектора E.
Рассмотрим теперь волну 2, бегущую вдоль другого главного направления, например, вдоль оси . Две компоненты волны - и - имеют вид
- 1 , - 2
В первой из этих волн вектор E колеблется в главной плоскости (параллельно оптической оси ). Эта волна необыкновенная, ее фазовая скорость . . отличается от фазовой скорости второй, обыкновенной волны 8 8, соответственно, отличаются волновые числа и : . 2$ .,
2$ 8, где — длина волны в вакууме. В соответствии с принятой терминологией, показатели преломления . и 8 называются соответственно необыкновенным и обыкновенным.
Проникая в кристалл на глубину , волны приобретают разность фаз 2$ . 8 . Пусть пластинка вырезана из одноосного кристалла параллельно оптической оси (как показано на рис. 10.3), толщина пластинки . Пучок света падает на нее по нормали, т. е. бежит вдоль оси . Тогда на выходе из пластинки возникает дополнительная разность фаз, равная
|
2 |
. 8 |
(10.3) |
|
|||
|
|
|
|
Если толщина такова, что |
|
||
2$ , где — целое число, |
(10.4) |
||
2 |
|
|
|
то такая пластинка называется пластинкой в 4, или четвертьволновой пластинкой.
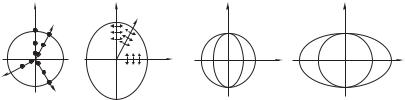
Пусть на входе в пластинку (при 0) колебания - и - синфазны. Так происходит, если на пластинку падает линей- но-поляризованная волна, в которой плоскость колебаний лежит в первом и третьем квадрантах (рис. 10.4 а). Тогда на выходе (при ) разность фаз равна $ 2. Мы получаем эллиптически поляризованную волну, причем главные оси эллипса совпадают с осями и . Если, кроме того, плоскость колебаний вектора E на входе составляет угол 45Æ с осями и , то амплитуды волн - и - одинаковы и на выходе получаем свет, поляризованный по кругу.
Если
$ 2$ , |
(10.5) |
то пластинку называют пластинкой в 2. Линейно-поляризованная на входе в пластинку волна с син-
фазно колеблющимися составляющими - и - останется на выходе линейно-поляризованной, причем колебания - и - ста-

660 |
Волны в анизотропных средах. Элементы кристаллооптики [ Гл. 10 |
||||||
сталла ( . & 8 — сфера лежит внутри эллипсоида, рис. 10.6 б). |
|||||||
В любом случае точки касания сферы и эллипсоида лежат на |
|||||||
оптической оси. |
|
|
|
||||
10.3. Преломление на границе анизотропной среды, |
|||||||
|
|
|
|
двойное лучепреломление |
|
||
|
Ранее мы рассмотрели, как ведет себя луч света, падающий |
||||||
нормально на кристаллическую пластинку, вырезанную парал- |
|||||||
лельно оптической оси (т. е. оптическая ось параллельна по- |
|||||||
верхности, на которую падает луч света): направление распро- |
|||||||
странения луча не меняется, а анизотропия проявляется в том, |
|||||||
что |
скорость |
волны оказывается |
различной для волн разной |
||||
à |
|
|
d |
|
ориентации вектора |
E (обыкно- |
|
M |
|
N |
венная волна, в которой век- |
||||
|
|
|
|||||
|
A |
B |
C |
D |
тор E перпендикулярен оптиче- |
||
|
|
|
|
|
ской оси, бежит со скоростью |
||
|
|
|
|
|
8, и необыкновенная, в кото- |
||
Îïò. |
|
|
|
рой вектор E параллелен опти- |
|||
îñü |
|
|
|
ческой оси, бежит со скоростью |
|||
á |
|
|
|
|
.). |
особенно- |
|
M |
|
|
N |
|
Проиллюстрируем |
||
|
A |
B |
C |
D |
сти |
возможных более сложных |
|
|
|
|
|
|
ситуаций на следующем примере. |
||
Îïò. |
|
|
|
|
Пусть на поверхность одноосно- |
||
|
|
|
|
го |
кристалла падает |
нормально |
|
îñü |
|
|
|
|
|||
|
|
|
|
|
луч света с поперечным сечени- |
||
|
|
|
|
|
ем |
(рис. 10.7). Оптическая ось |
|
|
|
|
|
|
кристалла составляет угол # |
||
|
|
|
|
|
с поверхностью и лежит в плос- |
||
|
|
|
Рис. 10.7 |
кости рисунка, поэтому эта плос- |
|||
|
|
|
|
|
кость является главной плоско- |
||
стью кристалла. Будем считать падающий на кристалл свет |
|||||||
естественным, в котором содержится как компонента вектора E, |
|||||||
лежащая в плоскости падения, так и перпендикулярная плоско- |
|||||||
сти падения. |
|
|
|
|
|||
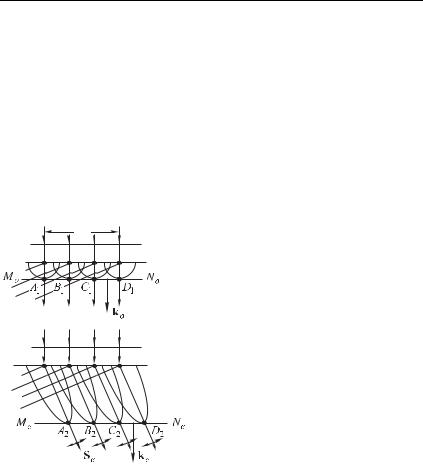
|
Определим направление волн в кристалле, используя постро- |
||||||
ение Гюйгенса. |
|
|
|
||||
|
Волновая поверхность ! в падающей волне (перпендику- |
||||||
лярная направлению распространения и следовательно, парал- |
|||||||
лельная поверхности кристалла) одновременно достигает всех |
|||||||
точек поверхности (от до E) возбуждая в диэлектрике вто- |
|||||||
ричные волны. Источниками этих вторичных волн являются воз- |
|||||||
буждаемые падающей волной осцилляторы среды, находящиеся |
|||||||
в точках поверхности от до E. Рассмотрим сначала обыкно- |
|||||||
