студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

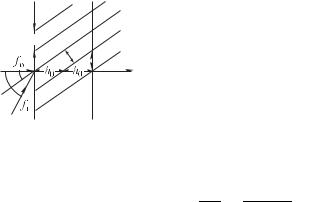
среды–фотоэмульсии. Рассмотрим теперь, какие возможности открывает объемная регистрирующая среда. Чтобы понять, когда и почему начинает играть роль третье измерение — толщина фоторегистрирующей среды, — посмотрим, каков результат интерференции двух плоских волн, если рассматривать его не только на плоскости , но и по толщине, вдоль оси . Итак, пусть в фотоэмульсии распространяются две волны. Заметим, что до фотообработки (проявления) фотоэмульсия прозрачна. Одну из волн, бегущую вдоль оси , 7о D будем счи-

тать опорной, а вторую 7п D ' ' , волновой вектор которой составляет угол # с осью , — предметной волной

(при этом мы имеем в виду, что любую предметную волну можно представить в виде суперпозиции плоских волн разных направлений #). Легко найти интенсивность суммарной вол-

ны : , 7о 7п 2 4 2 2 #2 1 # 2 . Максимумы интенсивности располагаются вдоль плоскостей

Перемещаясь вдоль оси на расстояние 0 2, мы перейдем из максимума в минимум.

В максимумах, где интенсивность суммарной волны велика, велико химическое воздействие света на среду, в минимумах воздействие света мало. Будем полагать, что плоскости, где интенсивность света велика, становятся после обработки подобными частично отражающим свет зеркалам. Плоскости, где интенсивность близка к нулю, после обработки полностью прозрачны.

8.15 ] Объемная голограмма 633

Итак, в результате обработки в фотоэмульсии образуется набор «зеркал», частично отражающих, а частично прозрачных для

Фотообработка проэкспонированной голограммы может производиться и таким образом, что от интенсивности света при экспозиции будет зависеть не отражающая способность слоев фотоэмульсии, а их оптическая плотность (коэффициент преломления ). В этом случае объемная решетка оказывается фазовой.

Толщина фоторегистрирующей среды никак не будет проявляться, если она заметно меньше величины 0 2: ведь в этом случае тонкий луч света, проходя через среду, не будет пересекать слои различной прозрачности. Такая голограмма аналогична тонкому экрану. Наоборот, при толщине, много большей 0, луч света, бегущий вдоль оси , много раз пересекает слои разной прозрачности, частично проходя сквозь каждый слой — зеркало, а частично отражаясь от него. Итак, эффект объемности фоторегистрирующей среды проявляется, если ее толщина превышает

Из последнего условия ясно, что один и тот же слой фотоэмульсии можно считать тонким или толстым, в зависимости от того, как организован эксперимент. Если волны сходятся под малым углом #, то 0 2#2 велико, толщина данного фотослоя оказывается много меньше 0 и голограмма получается тонкой. Именно так записывается голограмма по методу Габора или Лейта–Упатниекса.

Голографические фотослои имеют толщину от нескольких микрометров ( 10 4 см) до нескольких десятков микрометров ( 10 3 см) (длина волны зеленого цвета 0,5 мкм). В схеме Лейта–Упатниекса углы схождения волн порядка и меньше 0,1 рад, поэтому параметр 0 имеет величину порядка и более 100 мкм, т. е. ' 0 — условие (8.117) не выполняется. Как уменьшить параметр 0? Кардинальный способ — осветить слой фотоэмульсии с разных сторон. Тогда угол # приближается к $, а величина 0 — к 2. При этом на той же толщине фотоэмульсии укладывается много зеркальных слоев, возникающих после обработки. То есть восстанавливающая волна, бегущая на стадии реконструкции (восстановления) изображения вдоль оси , испытывает много отражений от этих слоев, образующих объемную решетку. Схема получения объемной голограммы, предложенная советским ученым Ю. Н. Денисюком (р. 1927), показана на рис. 8.63. Излучение направляется на фотопластинку, за которой расположен голографируемый объект. Свет свобод-

634 Дифракция [ Гл. 8

но проходит сквозь прозрачную фотоэмульсию, отражается от предмета и вновь проходит через слой фотоэмульсии. Прямой лазерный пучок, проходящий через фотоэмульсию слева направо — это опорная волна, а отраженный от предмета и идущий ему навстречу — это предметная

нувшись к простому примеру, когда предметной волной является плоская волна, составляющая угол # с осью , а опорной — плоская волна, бегущая вдоль оси . Итак, пусть восстанавливающая волна — плоская волна, бегущая вдоль оси , падает на

%% показаны на рис. 8.64). Обратим внимание на то, что отражается восстанавливающая волна в направлении, точно совпадающим с направлением предметной волны, которая падала на голограмму в процессе записи (ее интерференция с опорной волной и образовала эту систему зеркальных слоев), поскольку угол падения на зеркало равен углу отражения. Существенно при этом, что волны 1, 2, 3, ..., отраженные разными «зеркалами», интерферируют. Каков результат интерференции?

Найдем разность хода волн, отраженных от двух соседних зеркал и (расстояние между слоями — период объемной решетки — определяется формулой (8.116)). Волна 2, отраженная от зеркала , проходит оптический путь!, в то время как волна 1, отраженная от зеркала, проходит путь . Если точки ! и лежат в одной плоскости, перпендикулярной направлениям отраженных волн

8.16 ] Чем отличается голографическое изображение от фотографии 635

(т. е. на одной волновой поверхности), то это означает, что колебания в плоскости !, созданные волнами 1 и 2, синфазны, а значит разность оптических путей ! равна длине волны , используемой при восстановления изображения:! . Легко убедится, что последнее условие можно записать в виде

Это — условие интерференционного отражения волны объемной решеткой с периодом , где * — угол скольжения (угол

между падающей волной и плоскостями решетки). Оно называется условием Брэгга–Вульфа (по имени английского физи-

ка Л. Брэгга (1890–1971) и российского физика Г.В. Вульфа (1863–1925)). Если длина восстановливающей волны такова, что выполняется условие Брэгга–Вульфа, то волны, отраженные от разных зеркальных слоев решетки, оказываются синфазными — возникает сильное отражение — восстанавливается предметная волна. Вспомнив, что период решетки определяется формулой (8.116), а * #2, находим: сильное интерференционное отражение возникает лишь на длине волны , совпада-

ющей с длиной волны , используемой при записи голограммы. Мы видим, что объемная голограмма обладает спектральной избирательностью — она «запоминает» цвет — длину волны

света, с помощью которого записывается голограмма. Если восстанавливать голограмму белым светом, то объемная решетка «выбирает» из белого света лишь ту спектральную компоненту, которая использована при записи. Это свойство объемной голограммы используется для записи голограмм художественных произведений: при этом добиваются великолепной цветопередачи при восстановлении изображения белым светом. Отметим еще одно важное свойство голограммы: при большом числе отражающих зеркальных слоев, составляющих объемную решетку, интенсивность восстановленной волны оказывается близкой к интенсивности волны, падающей на голограмму при реконструкции изображения; другими словами, практически весь световой поток преобразуется объемной голограммой в волну, образующую единственное мнимое изображение.

8.16. Чем отличается голографическое изображение от фотографии

При фотографировании каждая точка предмета рассеивает сферическую волну, которая с помощью объектива фотоаппарата фокусируется в небольшое пятнышко на фотопластине. Так как отражательная способность разных точек объекта различна, то различна и интенсивность света, падающего на разные участ-

ки фотопластинки. Почернение разных участков фотопластинки после фотообработки (которое пропорционально интенсивности), повторяет распределение яркости на предмете — мы получаем негативное изображение.

Отметим три особенности фотографического изображения. Во-первых, на фотопластинке фиксируется лишь распределение интенсивности и, следовательно, фотоизображение содержит неполную информацию о предмете (нет распределения фаз и в частности, нет рельефа предмета). Во-вторых, на каждом небольшом участке фотопластинки получается изображение лишь небольшого («сопряженного») участка предмета. В-третьих, трехмерные объекты регистрируются в виде плоских двумерных изображений.

Голограмма, как мы видели, сохраняет полную информацию об объекте: возникающий на ней интерференционный узор зависит как от амплитуды, так и от фазы предметной волны.

Наблюдатель, который при восстановлении смотрит сквозь голограмму (как в окно), видит как бы реальный предмет; так, изменяя положение, наблюдатель может увидеть те детали объекта, которые не были видны (затенены другими деталями) ранее — голографическое изображение трехмерно. Важнейшее свойство голограммы состоит в том, что любой ее малый участок содержит информацию обо всем объекте: ведь поле в каждой точке голограммы является суперпозицией полей, посылаемых всеми точками предмета (и опорной волной).

Другими словами, интерференционная картина на каждом небольшом участке голограммы содержит информацию об амплитуде и фазе колебаний всех точек предмета, поэтому изображение может быть восстановлено с помощью небольшого осколка голограммы, полученной при записи. Разумеется, разрешающая способность определяется размером осколка.

Вопросы и задачи

1. Найти спектр плоских волн за синусоидальной решеткой с амплитудным коэффициентом пропускания 1 G 1 , освещаемой нормально падающей плоской волной.

2. Плоский монохромотический пучок света с длиной волны дифрагирует на двух последовательно расположенных синусоидальных решетках

с амплитудным коэффициентом пропускания 1 2 1 2 1 . При смещении одной из решеток вдоль оси со скоростью интенсивность

нулевого дифракционного максимума периодически изменяется. Определить частоту этих изменений, а также отношение максимальной и минимальной интенсивностей.

3. Диск из стекла с показателем преломления закрывает полторы зоны Френеля для точки наблюдения 6. При какой толщине диска освещенность

в точке 6 максимальна?

Ответ: 2 5 4 2 1 ( 0, 1, ...).

4.Какова интенсивность волны в центре картины дифракции на круглом непрозрачном экране, если он закрывает 1) одну зону Френеля, 2) две зоны Френеля, 3) 4,5 зоны Френеля?

5.Показать, что если точечный источник света находится на расстоянии от непрозрачного экрана с отверстием, а точка наблюдения — на расстоянии ) от него, то радиус -й зоны Френеля определяется формулой

% ) ) .

6.Точечный источник света и точка наблюдения 6 расположены симметрично на расстоянии 2 друг от друга на оси круглого отверстия в непрозрачном экране. Отверстие оставляет открытой одну зону Френеля. Во сколько раз изменится интенсивность света в точке 6, если к отверстию без нарушения осевой симметрии приложить тонкую линзу с фокусным расстоянием 2 .

7.Оценить, с какого расстояния можно увидеть раздельно свет от двух фар автомобиля.

8.Коллиматорная щель (, освещаемая источником света, находится в фокусе линзы с фокусным расстоянием 2 20 см. Пройдя через линзу, свет

полностью использована разрешающая способность решетки в окрестности длины волны 500 нм?

9.С помощью интерферометра Фабри–Перо исследуется выделенный системой фильтров участок спектра шириной 1,2 нм. Минимальная разность длин волн соседних спектральных линий 0,001 нм. Оценить максимальное значение коэффициента пропускания зеркал, при котором можно исследовать этот участок спектра.

10.Два пучка белого света, полученные от одного точечного источника, сходятся на входной щели регистрирующего спектрального прибора. Разность хода равна 300 м. Оценить разрешающую способность спектрального прибора, который может обнаружить интерференцию этих пучков.

Ответ: 5 108

11.Линза с фокусным расстоянием 2 50 см и диаметром = 5 см освещается параллельным пучком света ( 630 нм). Во сколько раз интен-

сивность волны + в фокусе линзы больше интенсивности +0 падающей на линзу волны? Оценить размер пятна в фокальной плоскости линзы.

12.Камера с малым отверстием глубиной 10 см предназначена для фотографирования удаленных объектов. Оценить диаметр отверстия, при котором она имеет максимальную разрешающую способность, 500 нм.

13.При аэрофотосъемке местности используется объектив с фокусным расстоянием 2 10 см и диаметром = 5 см. Съемка производится на

фотопленку, имеющую разрешающую способность 100 мм 1. Определить, какие детали местности могут быть разрешены на фотографиях, если съемка производится с высоты 10 км.

14. Оценить расстояние , с которого можно увидеть невооруженным глазом свет лазера, генерирующего в непрерывном режиме мощность 610 Вт на частоте @ 4 1015 Гц, если для формирования луча используется параболическое зеркало диаметром = 50 см. Глаз видит источник в зеленой части спектра, если в зрачок (диаметра 5 мм) попадает 60 квантов в секунду.

Г л а в а 9

ДИСПЕРСИЯ ВОЛН

9.1. Фазовая и групповая скорость. Формула Рэлея

Приступая к изучению волновых процессов, мы ввели понятие фазовой скорости волны — скорости, с которой перемеща-

ются волновые поверхности (поверхности с фиксированным значением фазы колебаний). Это понятие применимо к монохроматической волне с заданной частотой , бесконечно протяженной в пространстве и во времени. Реальный волновой процесс всегда ограничен во времени, а это означает, что он представляется суперпозицией волн различных частот . При этом различные гармонические составляющие суммарного волнового процесса могут иметь разные фазовые скорости.

Наблюдаемая зависимость фазовой скорости от частоты называется дисперсией. Среда, в которой возникает дисперсия, называется диспергирующей средой. Зависимость называют законом дисперсии. Часто закон дисперсии среды

задают в виде зависимости волнового числа от частоты:или зависимости показателя преломления от частоты: . Для описания процесса распространения

волн в диспергирующей среде возникает необходимость ввести новую характеристику, называемую групповой скоростью.

Поясним физический смысл этого понятия на следующем примере. Пусть некоторый излучатель является источником сигнала 7 D#0 (пусть, например, эта функция описывает изменение электрического поля вблизи излучателя), где 0 — частота несущего колебания, — закон модуляции, который и содержит передаваемое сообщение. Возникшая при этом электромагнитная волна начинает распространяться в диспергирующей среде и через некоторое время достигает приемной антенны, находящейся на расстоянии от излучателя. Будем считать, что сигнал имеет конечную длительность >, причем на протяжении большого числа периодов несущего колебания 2$ 0 функцияостается практически неизменной, т. е. характерное время

ее изменения > много больше периода несущей: > 2$ 0.

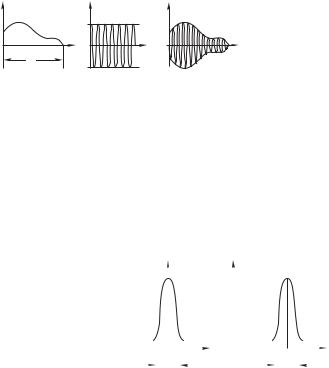
в показан пример сигнала 7 , который представляет собой произведение медленно меняющейся «огибающей»длительности > — функции, равной тождественно нулю

вне интервала времени >, большим по сравнению с периодом несущего колебания > 2$ 0 (рис. 9.1 а), и быстро осциллирующей гармонической функции D#0 . Разумеется, на графике

Рис. 9.1

рис. 9.1 б показана Re D#0 , т. е. косинусоида. Представим закон модуляции в виде суммы гармонических колебаний различных частот

где — спектр (преобразование Фурье) функции , показанный на рис. 9.2 а.

Поскольку изменения функции медленные в масштабе периода несущей, ширина ее спектра , равная согласно соот-

находим

%0 ,

т.е. спектр сигнала 7 можно получить из спектра «огибаю-

щей» , перенося последний по оси частот на величину 0, как показано на рис. 9.2 б.

Каждой гармонической составляющей «огибающей» , имеющей низкую частоту , соответствует гармоническая

составляющая сигнала 7 высокой частоты 0 , причем 0 , поскольку все низкие частоты , составляющие

0 0 0 0

Далее, экспоненциальный множитель D #0 0 , не зависящий от переменной , можно вынести из под знака интеграла.