
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
614 |
|
|
Дифракция |
|
|
[ Гл. 8 |
|||
|
Сравнив полученную формулу с выражением |
|
|||||||
|
|
|
, |
2 2 , |
|
(8.103) |
|||
|
|
|
|
|
2 2 |
|
|
|
|
описывающим распределение фаз колебаний в сходящейся сфе- |
|||||||||
рической волне (см. § 4.1), находим |
|
|
|
||||||
|
|
|
|
1 1 1 |
|
|
(8.104) |
||
|
|
|
|
1 |
2 |
2 |
|
|
|
|
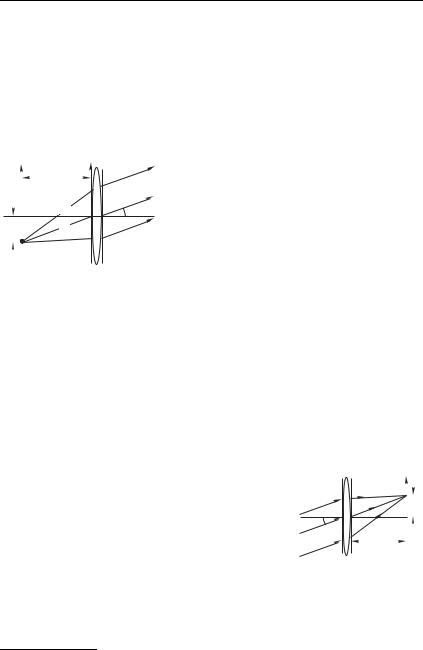
Функция , описывает форму волнового фронта в схо- |
||||||||
дящейся волне, если 2 & 0, что соответствует действительному |
|||||||||
|
x |
|
|
изображению (рис. 8.44). При 2 ' 0 |
|||||
|
|
|
формула |
(8.103) |
описывает |
расходя- |
|||
|
(x) |
(x) |
|
||||||
|
|
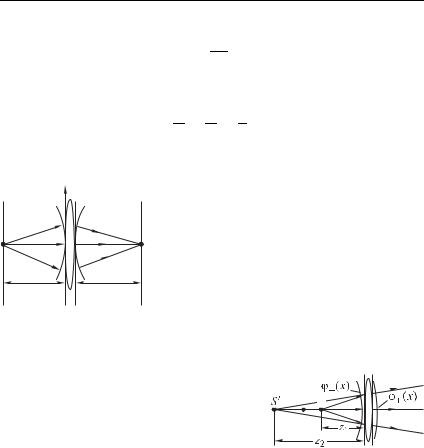
щуюся волну, при этом изображение |
|||||||
|
|
|
|
||||||
|
|
|
|
оказывается мнимым (рис. 8.45). |
|||||
|
|
|
|
Аналогичным образом можно пока- |
|||||
S |
O |
O |
S |
зать, что формула линзы (8.104) спра- |
|||||
|
z1 |
z2 |
|
ведлива для любой точки 9, располо- |
|||||
|
|
женной недалеко |
от |
оптической оси, |
|||||
|
z 0 |
z 0 |
|
||||||
|
|
т. е. для предметов малого размера. |
|||||||
|
|
|
|
||||||
|
Рис. 8.44 |
|
Формирование изображения с помо- |
||||||
|
|
щью линзы можно рассматривать, осно- |
|||||||
|
|
|
|
||||||
вываясь на идее пространственного спектрального разложения. |
|||||||||
Такой подход аналогичен спектральному анализу процесса вы- |
|||||||||
нужденных колебаний в линейной ко- |
|
|
|
||||||
лебательной системе (например, в ко- |
|
|
|
||||||
лебательном контуре). Напомним, что |
|
S |
|
||||||
спектральный анализ основан на пред- |
|
|
|
||||||
ставлении внешнего воздействия, воз- |
|
|
|
||||||
буждающего вынужденные колебания, |
|
|
|
||||||
в |
виде суперпозиции |
гармонических |
|
Рис. 8.45 |
|||||
колебаний разных частот. |
|
|
|
|
|
||||
|
Представим монохроматическую волну, идущую от предмета, |
||||||||
в виде суперпозиции плоских волн разных направлений #, т. е. |
|||||||||
разных пространственных частот 4 #. Каждая гармони- |
|||||||||
ка — плоская волна определенного направления — фокусируется |
|||||||||
линзой в «свою» точку фокальной плоскости, в которой возника- |
|||||||||
ет, таким образом, картина пространственного спектра: амплиту- |
|||||||||
да и фаза колебаний в точке 0 фокальной плоскости однозначно |
|||||||||
определяется амплитудой и фазой колебаний той плоской волны, |
|||||||||
которая в эту точку фокусируется. По этой причине фокальную |
|||||||||
плоскость линзы называют фурье-плоскостью. По терминологии |
|||||||||
немецкого инженера и оптика Э. Аббе, впервые предложившего |
|||||||||
такой подход, поле в фокальной плоскости называют первичным |
|||||||||
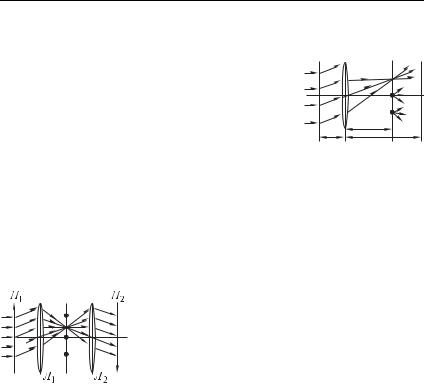
изображением. На рис. 8.46 показана ситуация, когда предме- |
|||||||||
том является решетка, освещаемая плоской нормально падающей |
|||||||||
8.11 ] |
Оптическое изображение и пространственная фильтрация |
615 |
||||||
волной. При этом в фурье-плоскости, как мы знаем, возникает |
||||||||
картина фраунгоферовой дифракции: набор ярких точек — диф- |
||||||||
ракционных максимумов. Итак, в процес- |
|
|
|
|||||
се распространения света от предмета до |
|
Ô |
|
|||||
фурье-плоскости осуществляется преобра- |
|
|
|
|||||
зование Фурье светового поля (по термино- |
|
|
|
|||||
логии Аббе, первая дифракция). |
|
f |
|
|||||
Далее каждая |
точка фурье-плоскости |
z1 |
z2 |
|||||
|
||||||||
(каждый дифракционный максимум) рас- |
|
|||||||
|
|
|
||||||
сматривается |
как |
источник |
сферической |
Рис. 8.46 |
|
|||
волны. Все сферические волны, исходя- |
|
|||||||
|
|
|
||||||
щие из разных точек фурье-плоскости, интерферируя, образуют |
||||||||
в плоскости, находящейся на расстоянии 2 за линзой, собствен- |
||||||||
но изображение объекта. Это изображение Аббе назвал вторич- |
||||||||
ным, а процесс распространения света от фурье-плоскости до |
||||||||
плоскости изображения — второй дифракцией. |
|
|
||||||
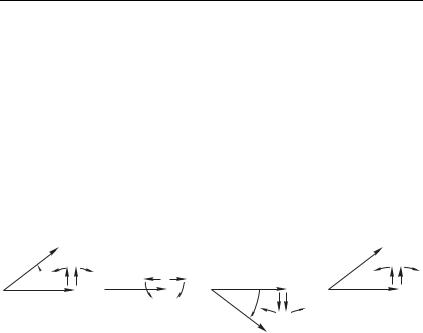
Особенно наглядно принцип двойной дифракции проявляется |
||||||||
в оптической схеме, показанной на рис. 8.47. Схема состоит из |
||||||||
|
Ô |
|
двух линз с общей |
фокальной |
плоско- |
|||
x |
|
стью Ф. Задняя фокальная плоскость лин- |
||||||
|
|
|||||||
|
|
зы Л1 совпадает с передней фокальной |
||||||
|
|
|
||||||
|
|
|
плоскостью линзы Л2. В этом случае пер- |
|||||
O |
O |
O |
вая дифракция — это распространение |
|||||
|
|
x |
света от передней фокальной плоскости |
|||||
|
|
линзы Л1, где расположен предмет (плос- |
||||||
|
|
|
||||||
|
Рис. 8.47 |
|
кость П1 на рис. 8.47), к плоскости Ф, |
|||||
|
|
где возникает картина пространственного |
||||||
спектра — первичное изображение. Далее, сферическая волна |
||||||||
идущая из любой точки фурье-плоскости, преобразуется линзой |
||||||||
Л2 в плоскую волну. Таким образом, каждая плоская волна иду- |
||||||||
щая от предмета, преобразуется системой двух линз в плоскую |
||||||||
волну, приходящую к плоскости изображения (задней фокальной |
||||||||
плоскости П2 линзы Л2). Причем, как видно из рис. 8.47, если |
||||||||
фокусные расстояния линз одинаковы, то волна с пространствен- |
||||||||
ной частотой 4 # преобразуется в волну с пространствен- |
||||||||
ной частотой « 4» ( -компонента вектора k изменяет знак). Это |
||||||||
приводит к инверсии — изображение оказывается перевернутым. |
||||||||
Можно сказать, что в процессе образования изображения проис- |
||||||||
ходит два последовательных преобразования Фурье: от входной |
||||||||
плоскости П1 к фурье-плоскости Ф — первая дифракция, и затем |
||||||||
от фурье-плоскости с помощью линзы Л2 к выходной плоскости |
||||||||
П2 — вторая дифракция. |
|
|
|
|
||||
Особая роль фурье-плоскости обусловлена тем, что именно |
||||||||
в этой плоскости возможно избирательное воздействие на раз- |
||||||||
ные пространственные гармоники: установив в любой точке 0 |
||||||||
фурье-плоскости маленькую пластинку, вносящую определенное |
||||||||
616 |
Дифракция |
[ Гл. 8 |
поглощение и (или) фазовую задержку, мы изменим амплитуду и (или) фазу плоской волны с пространственной частотой 4 0 7, не изменяя амплитуд и фаз других плоских волн. Устанавливая в фурье-плоскости различные амплитудно-фазовые маски, можно направленно изменять пространственный спектр изображения, влияя таким образом на его характеристики. Этим путем можно решать самые разнообразные задачи: улучшение качества изображений, разрешающей способности оптических систем, визуализация фазовых объектов, выполнение самых разнообразных преобразований пространственной структуры световых полей и т. д., т. е. решать широкий круг задач оптической обработки информации.
Визуализация фазовых объектов. В качестве примера рас-
смотрим проблему визуализации фазовых объектов, которую можно решить, используя метод фазового контраста, предло-
женный Цернике. Пусть фазовый объект — тонкая прозрачная пластинка, имеющая разный в разных точках показатель преломления (или толщину), но не изменяющая амплитуду прошедшей волны, находится во входной плоскости П1 оптической системы, показанной на рис. 8.47. Функция пропускания такой пластинкиD , где ( — толщина, — распределение показателя преломления). При освещении пластинки (фазового объекта) плоской, нормально падающей волной, комплексная амплитуда волны в плоскости, примыкающей к пластинке справа, согласно (8.3), есть 70 D . Если оптическая система идеальна, то комплексная амплитуда в выходной плоскости П2 тождественно повторяет (с точностью до инверсии) входное поле 70 , а наблюдаемая картина интенсивности :0 70 2 1, т. е. в плоскости П2 мы наблюдаем равномерную засветку: информация о фазовой структуре предмета потеряна, фазовый объект не видим.
Для визуализации фазового объекта Цернике предложил установить в фурье-плоскости, на оптической оси, маленькую фильтрующую пластинку, которая, не изменяя амплитуды прошедшей волны, вносит фазовую задержку, равную $ 2. Проанализируем структуру светового поля в выходной плоскости П2, рассмотрев в качестве примера объект — фазовую синусоидальную решетку с малой глубиной модуляции ( 1). В этом случае
70 D 1 1 CD |
CD |
|
2 |
2 |
|
|
|
(8.105) |
Итак, входное поле представляется в виде суммы трех слагаемых, в соответствии с этим, от входной плоскости П1 вправо распространяются три плоские волны. Первое слагаемое ответственно за появление плоской волны единичной амплитуды
8.11 ] Оптическое изображение и пространственная фильтрация 617
71 , D , бегущей вдоль оси оптической системы (оси ). Второе и третье слагаемые — плоские волны с амплитудой 2, направления распространения которых составляют углы # с оптической осью, где # (т. е. и — пространственные частоты этих волн). Обратим внимание, что в точке 0 входной плоскости колебание первой волны отличается по фазе на $ 2 от колебаний двух наклонных волн (обратите внимание
на множитель D 2).
Три слагаемых в (8.105) — это три гармонических колебания или, если угодно, три комплексных числа, которые можно изобразить в виде векторов. На рис. 8.48 a показано положение этих векторов в начале координат ( 0). Горизонтальный вектор единичной длины изображает колебание, созданное осевой волной, два вектора длины 2 1, повернутые на угол $ 2 — колебания боковых волн. При смещении из точки 0
m
m
à |
á |
â |
ã |
Рис. 8.48
перпендикулярно оси , фаза колебания осевой волны не меняется, поэтому соответствующий вектор остается горизонтальным. Фазы боковых (наклонных) волн изменяются: , поэтому изображающие векторы поворачиваются (по и против часовой стрелки). На рис. 8.48 б показано положение векторов в точке, где $ 2: векторы повернулись на угол $ 2, а на рис. 8.48 в в точке , где $, векторы повернулись на угол $. При смещении на расстояние, равное периоду решетки2$ , восстанавливается исходное расположение векторов (рис. 8.45 г). Легко видеть, что суммарный вектор, не меняя своей длины (с точностью до величины порядка 2) изменяет угол наклона от до , что и соответствует фазовой структуре волнового поля. Обратите внимание на полную аналогию с векторным изображением колебания, модулированного по фазе (см.§ 1.5).
Осевая плоская волна, фокусируясь линзой в начало координат фурье-плоскости (0 0) проходит через фазовую фильтрующую пластинку, а две наклонные волны, фокусируясь в точки 01, 2 7# 7 , не «задевают» пластинку. Далее линза Л2 преобразует сферические волны, исходящие из точек 0 0 и 01, 2 7 , в плоские волны, которые, интерферируя, образуют изображение.
618 |
Дифракция |
[ Гл. 8 |
Наличие маленькой фазовой пластинки в фурье-плоскости на оптической оси приводит к относительной фазовой задержке в $ 2 осевой волны (относительно боковых наклонных волн), поэтому поле выходной плоскости можно записать в виде
|
7 D 2 C D |
C D , |
||
или |
|
2 |
2 |
|
|
|
|
||
7 |
1 D |
D |
|
1 |
|
2 |
2 |
|
|
Изменение фазовых соотношений между осевой и наклонными волнами иллюстрируют векторные диаграммы, показанные на рис. 8.49. Поворот вектора еди- 


 ничной длины (изображающего коле-
ничной длины (изображающего коле- 
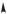 бания осевой волны) на $ 2 приводит к тому, что в точке 0 все три изображающих вектора оказыва-
бания осевой волны) на $ 2 приводит к тому, что в точке 0 все три изображающих вектора оказыва-
x 0 x ( /2)/ x / ются коллинеарными. При смещении |
||
Рис. 8.49 |
из начала координат изменяется фаза |
|
боковых волн. |
||
|
||
Как видно из векторных диаграмм, длина суммарного вектора при смещении по координате изменяется, а угол наклона (ориентации) суммарного вектора остается неизменным, что и соответствует чисто амплитудной структуре, т. е. полю с плоским волновым фронтом и меняющейся от точки к точке амплитудой. Таким образом, метод фазового контраста позволяет преобразовать исходную фазовую решетку в амплитудную решетку в плоскости изображения.
Наблюдаемая картина интенсивности имеет вид
: 7 2 1 2 1 2
(с самого начала, благодаря условию 1, членами порядка2 и выше мы пренебрегаем). Итак, фазовые изменения входного поля 70 оказались визуализированы: мы наблюдаем изменения интенсивности, повторяющие изменения фазы входного поля. Обратите внимание на аналогию описанного здесь метода фазового контраста с методом преобразования колебания, моду-
лированного по фазе, в амплитудно-модулированное колебание (так называемый прием с изменением фазы несущей, см. § 1.5).
Читатель может самостоятельно проанализировать «метод темного поля». В этом методе вместо фазовой пластинки в $ 2 в фурье-плоскости на оптической оси устанавливается непрозрачный маленький экран. Осевая плоская волна, фокусируясь линзой в начало координат фурье-плоскости, поглощается непрозрачным экраном и не участвует в формировании изображения. Боковые же волны остаются без изменения. Какова в этом случае картина интенсивности в выходной плоскости?
8.11 ] |
Оптическое изображение и пространственная фильтрация |
619 |
Метод темного поля аналогичен методу, который в радиотехнике используется для преобразования фазовой модуляции в амплитудную и называется «приемом без несущей».
Разрешающая способность оптических систем. Всякая реальная оптическая система отличается от идеальной по крайней мере одним важным обстоятельством: ее линзы имеют конечные размеры. Учет конечных размеров используемых объективов чрезвычайно важен для оценки предельных возможностей оптических систем. Необходимо иметь в виду, что функция пропускания линзы (8.12), о которой мы говорили ранее, правильно описывает преобразования волны линзой только в той области значений , которые находятся в пределах «зрачка» линзы. Если диаметр линзы E, то функция (8.12) справедлива
при 2 2 E2 2. Действительно, свет, проходящий «мимо» линзы, не представляет интереса, поскольку не участвует в формировании изображения. Все происходит так, как если бы идеальная бесконечная линза (функция пропускания которой описывается формулой (8.12)) была задиафрагмирована непрозрачным экраном с отверстием диаметра E, оставляющим открытой центральную часть линзы. Именно такая модель используется обычно для расчета дифракционных эффектов, связанных с конечным размером объектива.
Итак, пусть на линзу падает плоская волна, распространяющаяся вдоль оптической оси. Волна излучается удаленным источником, настолько удаленным, что в пределах площади зрачка,
т. е. в пределах диафрагмы диаметра E |
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 8.50), волновой фронт неотличим |
|
|
|
|
|
|
|
|
|
|
|
|
от плоского. |
|
|
|
|
|
|
|
|
|
|
|
0 |
Пройдя через диафрагму, волна па- |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|||
дает на идеальную (бесконечную) лин- |
|
|
|
|
|
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
зу. Изображенная на рисунке оптиче- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ская схема есть не что иное, как схе- |
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
ма наблюдения дифракции Фраунгофе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ра плоской волны на круглом отверстии |
|
|
|
|
|
Рис. 8.50 |
||||||
диаметра E. Мы уже отмечали, что для |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
наблюдения дифракции Фраунгофера на каком-либо препятствии достаточно установить за препятствием линзу — при этом картина в фокальной плоскости линзы подобна картине, которая возникает на большом расстоянии за препятствием ( E2 ).
Еще раз поясним, в чем суть дела. Плоская волна, пройдя через отверстие-диафрагму, уже не является плоской волной: за отверстием мы имеем непрерывный спектр плоских волн (т. е. набор плоских волн разных направлений). Каждая плоская волна из этого спектра фокусируется идеальной линзой в свою точку фокальной плоскости, в результате мы и получаем распределе-

620 Дифракция [ Гл. 8
ние интенсивности, показанное на рис. 8.51 — дифракционное
пятно (пятно Эйри), в котором концентрируется подавляющая |
||||
|
I |
доля светового потока, окруженное чередую- |
||
|
щимися светлыми (очень слабыми) и тем- |
|||
|
|
|
||
|
|
|
ными кольцами. Полуширина пятна Эйри |
|
|
I ( ) |
(см. (8.68)) |
|
|
|
|
|
00 1,22 2 |
(8.106) |
|
|
|
= |
|
|
|
|
Это и есть изображение бесконечно уда- |
|
0 0 |
||||
|
|
|
ленного точечного источника: изображение не |
|
Рис. 8.51
является точкой, как следует из законов гео-
метрической оптики, а представляет собой дифракционное пятно, причем чем больше размер объектива E, тем меньше дифракционное пятно, тем больше это пятно похоже на точку.
Следует подчеркнуть, что дифракционная формула (8.106) не приводит к правильному результату в пределе при E : при увеличении E пятно не становится как угодно малым. Мы уже подчеркивали, что бегущие волны не могут образовать в сумме световое поле, которое бы резко изменялось на расстояниях порядка длины волны. Пятно, размер которого существенно меньше длины волны, получить невозможно!
Поток энергии, падающий на линзу и равный :090, где :0 — интенсивность волны, 90 $E2 4 — площадь линзы, концентрируется в маленькое пятнышко, площадь которого равна
9 $02 |
2 |
. Средняя |
интенсивность |
волны в пятне |
||||
0 |
$ 7 E |
|||||||
Эйри оказывается при этом равной |
|
|
||||||
|
|
|
(0 +0 |
=4 |
(8.107) |
|||
|
: :0 |
( |
|
|
4 |
2 2 |
||
Для линзы диаметром 1 см с фокусным расстоянием 710 см выигрыш от фокусировки для длины волны 500 нм
(зеленый цвет) равен : :0 106! В реаль- |
|
|
|
|
|
ных линзах такой выигрыш достигается, если |
|
|
|
|
|
удается устранить аберрации, возникающие |
|
|
|
|
|
|
|
|
|
|
|
в линзах, поверхности которых имеют сфери- |
|
|
|
|
|
ческую (а не параболическую) форму. |
D |
|
|
|
|
|
|
|
|||
Дифракционная формула (8.106) с тем же |
|
|
|
|
|
успехом применима для оценки размера ди- |
|
|
|
|
|
фракционного пятна в фокусе параболическо- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
го зеркала диаметром E (рис. 8.52), посколь- |
|
Рис. 8.52 |
|||
ку распределение фаз колебаний в плоскости, |
|
||||
|
|
|
|
|
|
примыкающей к зеркалу (после отражения плоской волны от зеркала), аналогично фазовому распределению (8.11), которое обеспечивается линзой.
