студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf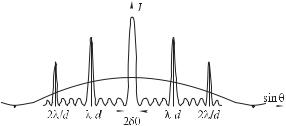
8.9 ] |
Дифракция Фраунгофера |
601 |
Первый сомножитель 7 2 описывает картину дифракции на щели (формула (8.66)). Второй сомножитель связан с интерференцией волн, приходящих от разных щелей к точке наблюдения.
Наиболее интересным в картине дифракции на решетке является наличие узких дифракционных максимумов, в которые идет подавляющая доля общего потока энергии.
Направления на эти максимумы определяются условием
1, 2, , |
(8.73) |
— волны от всех щелей решетки приходят в точку наблюдения с разностью хода , равной целому числу длин волн и, следовательно, создают синфазные колебания. Итак, разность фаз # 2$ . Амплитуда суммарного колебания оказывается при этом в ! раз больше амплитуды колебаний, созданных одной щелью: !7 , а интенсивность : !2 7 2 в !2 раз превышает интенсивность волны от одной щели, так как при # 2$ все векторы, составляющие цепочку векторов на рис. 1.7, оказываются коллинеарными, поэтому длина суммарного вектора в ! раз больше длины слагаемых векторов). Читатель может самостоятельно убедится, что второй сомножитель в (8.72) равен ! при условии (8.73):
|
B2 |
! |
(8.74) |
||
2 |
|
||||
' 2 |
|
|
|||
График функции (8.72) показан на рис. 8.35.
Штриховой линией показана «огибающая» — зависимость от первого сомножителя 7 2, описывающего картину фраунгоферовой дифракции на щели ширины .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/b |
|
|
|
|
|
|
|
|
|
|
|
|
/b |
|
|
|
|
|
|
|
|
|
|
Рис. 8.35
Для картины, изображенной на рис. 8.35, характерно, что уже при небольшом отклонении от направления (т. е. от направления, определяемого условием (8.73)) интенсивность резко уменьшается, обращаясь в нуль при Æ. Определить величину этого отклонения можно из следующих соображений.

602 |
Дифракция |
[ Гл. 8 |
В направлении векторная диаграмма имеет вид, показанный на рис. 8.36 а — цепочка, состоящая из ! коллинеарных векторов: # 2$ . Спрашивается, при каком отклонении Æ от направления век-
àторная диаграмма будет иметь вид, пока-
|
занный на рис. 8.36 б: замкнутая цепоч- |
|
ка векторов, в которой конец последнего |
N |
вектора совпадает с началом первого век- |
тора и, следовательно, длина суммарного вектора будет равна нулю. Чтобы вектор-
|
|
ная диаграмма, показанная на рис. 8.36 а, |
|
|
преобразовалась в замкнутый многоуголь- |
||
|
|
|
|
áник векторов рис. 8.36 б, необходимо, чтобы
Рис. 8.36 |
разность фаз колебаний от двух соседних |
|
щелей решетки в точке наблюдения изме- |
нилась на величину Æ# 2$!. Тогда (при ! 1) последний !-й вектор коллинеарен с первым: !Æ# 2$, т. е.
Æ |
|
2 |
или Æ |
|
|
(8.75) |
||
|
|
|
||||||
|
|
B |
B |
|
||||
Для сравнительно небольших углов можно приближенно |
||||||||
написать |
|
|
|
|
|
|
|
(8.76) |
|
Æ |
|
|
|
||||
|
|
|
|
|||||
|
|
|
|
B |
|
|
|
|
Это и есть оценка полуширины главных дифракционных максимумов. Целое число в (8.73) называется порядком главного максимума (или порядком дифракции). Например, при
1 имеем первый порядок дифракции; значению 1 отвечает минус первый порядок дифракции. Максимальное значение , как ясно из (8.73), ограничено величиной
|
|
(8.77) |
|
|
|
Реально же заметными являются лишь те дифракционные максимумы, которые лежат в пределах углов
, |
(8.78) |
) |
|
поскольку, как мы выяснили ранее, только в пределах этих углов в основном распространяется поток энергии от каждой из щелей решетки.
Поэтому (при & ) максимальный порядок можно оценить из условия (см. рис. 8.35)
или |
(8.79) |
|
) |
) |
|
8.10 ] Разрешающая способность спектральных приборов 603
При этом общее число главных дифракционных максимумов, в которые попадает подавляющая часть потока энергии, равно приблизительно 1 2 .
8.10. Разрешающая способность спектральных приборов
Ранее мы говорили о том, что излучение любого источника света можно представить как сумму волн различных частот (спектральное разложение).
Распределение энергии по спектру излучения (зависимость интенсивности от частоты : ) является чрезвычайно важной характеристикой, которая исследуется с помощью спектральных приборов. Мы рассмотрим несколько возможных способов.
Дифракционная решетка. Два обстоятельства позволяют использовать дифракционную решетку для спектральных измерений. Во-первых, как следует из (8.73), положение главных дифракционных максимумов зависит от длины волны, и во-вторых, ширина этих максимумов, как видно из (8.76), чрезвычайно мала, а поток энергии (интенсивность) велик при большом числе щелей решетки.
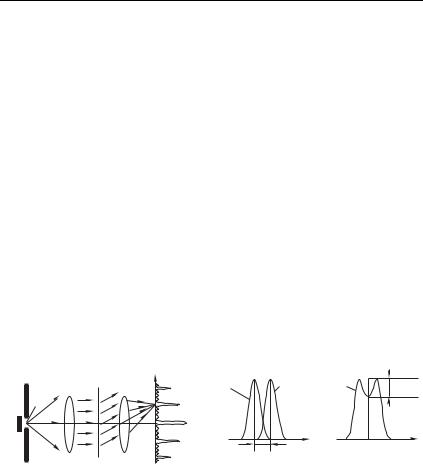
Схема спектрального прибора, основанного на использовании дифракционной решетки, показана на рис. 8.37 а.
|
x |
I1(x) |
I2(x) |
I(x) |
|
|
|
|
20 % |
D |
|
|
|
|
S |
0 |
|
x |
x |
|
|
|||
Ë1 |
Ë2 |
x = f |
|
|
|
à |
|
|
á |
Рис. 8.37
Излучение исследуемого источника 9 проходит через малую диафрагму (отверстие в непрозрачном экране) E, расположенную в фокальной плоскости объектива Л1. Сколлимированное объективом излучение (параллельный пучок света) падает на дифракционную решетку. При дифракции на решетке возникает ряд пучков, распространяющихся в направлениях , определяемых равенством (8.73). Угловая расходимость каждого из них Æ дается формулой (8.76). Следовательно, в фокальной плоскости объектива Л2 возникает картина дифракционных максимумов, положение которых (расстояние от оптической оси) есть
7 7 2 |
, |
|
|

604 |
Дифракция |
[ Гл. 8 |
а полуширина максимумов Æ 7Æ 7 ! |
; 7 — фокусное |
|
расстояние объектива Л2. |
|
|
|
Пусть излучение содержит две близкие спектральные линии |
|
и Æ одинаковой интенсивности. Положение -го дифракционного максимума, отвечающего длине волны , определяется условием
2
1 7 1
Соответственно, положение -го максимума для длины волны Æ есть
2 7 2 Æ 7
Какова минимальная величина Æ, при которой мы можем по наблюдаемой картине дифракции в фокальной плоскости линзы
Л2, зафиксировать наличие двух спектральных линий? Согласно критерию Рэлея предельно разрешимыми считают-
ся спектральные линии, для которых смещение дифракционных максимумов 2 1 7 Æ в точности равно их полуширине Æ 7 ! (в данном случае полуширина линии определяется по первому нулю интенсивности).
Эта ситуация показана на рис. 8.37 б. Слева изображены кривые интенсивности :1 и :2 , отвечающие -м максимумам для длин волн и Æ соответственно. Справа наблюдаемая в предельном случае суммарная картина интенсивности : :1 :2 . Как показывает расчет, основанный на формуле (8.72), в наблюдаемой картине : имеется примерно 20 %-ный провал, по наличию которого легко определить, что излучение источника содержит две спектральных линии. Разумеется, критерий Рэлея является условным: например, если расстояние между центрами картин :1 и :2 будет немного меньше величины Æ, то провал в суммарной картине будет несколько меньшим (например 15 % или 10 %), что визуально также можно определить. При достаточно малом смещении или существенно разной интенсивности линий провал в суммарной картине вообще может отсутствовать, однако и в этом случае наблюдаемая картина отличается от картины дифракции, создаваемой строго монохроматическим источником. Тем не менее, критерий Рэлея широко применяется для оценки возможностей спектральных приборов. Итак, используя критерий Рэлея Æ, находим
Æ ,
B
откуда получаем
|
! |
(8.80) |
|
Æ |
|||
|
|

8.10 ] |
Разрешающая способность спектральных приборов |
605 |
Отношение длины волны к предельно допустимому (со-
гласно критерию Рэлея) интервалу длин волн Æ называется
разрешающей способностью спектрального прибора. Высокая разрешающая способность дифракционных решеток
достигается за счет большого числа ! (до 105 и более). При этом общий рабочий размер решеток E ! не может быть слишком большим (обычно E 10 см), так как в противном случае возникают трудно выполнимые требования как к качеству объективов Л1 и Л2, так и к качеству самих решеток (равномерности нанесения штрихов). Расстояние между штрихами (период решеток ) при этом сильно ограничено: у хороших решеток величина составляет всего несколько длин волн (в оптическом диапазоне). Соответственно максимальная величина порядка дифракции , согласно (8.77), ограничена несколькими единицами. Из (8.80) и (8.77) следует, что максимальная величина разрешающей способности дифракционной решетки есть
|
|
|
! = |
(8.81) |
|
||||
Æ |
|
|
|
|
Из (8.81) получаем оценку минимально разрешимого интер- |
||||
вала длин волн |
|
2 |
|
|
|
|
Æ = |
(8.82) |
|
Имеется еще одна |
важная характеристика: |
максимальный |
||
спектральный интервал излучения, который может быть проанализирован с помощью спектрального прибора. Итак, пусть спектральный состав излучения содержит ряд компонент, лежащих в интервале от до (рис. 8.38). При этом разрешающая способность решетки достаточно высока, так что даже ближай-
шие линии в спектре излучения (с расстоя- |
I( ) |
|
|
|
|
|
|
|
||||||||
нием |
между |
ними |
Æ) разрешаются нашей |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
решеткой. Однако есть еще одна проблема. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Каждая спектральная компонента созда- |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
ет в |
фокальной плоскости |
объектива Л2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|||||||||||||||
(рис. |
8.37 а) |
свою |
картину |
дифракционных |
||||||||||||
|
Рис. 8.38 |
|||||||||||||||
максимумов. |
Пусть |
положение 1 -го |
|
|||||||||||||
максимума спектральной компоненты (находящейся на левом краю спектрального диапазона излучения источника) совпадает с положением -го дифракционного максимума спектральной компоненты (находящейся на правом краю спектрального диапазона излучения), т. е. выполняется условие:
1 |
(8.83) |
Ясно, что при этом наблюдаемая картина дифракции в фокальной плоскости объектива Л2 не дает возможности определить, наблюдается ли -й максимум для длины волны

606 |
|
|
|
Дифракция |
|
|
[ Гл. 8 |
или мы видим 1 -й максимум для длины волны . Равен- |
|||||||
ство (8.83) является предельным условием, при котором спек- |
|||||||
тральные максимумы разных порядков начинают перепутывать- |
|||||||
ся; спектральный диапазон, превышающий предельное значение |
|||||||
, определяемое условием (8.83), не может быть проанализи- |
|||||||
рован. Этот максимально допустимый диапазон называется |
|||||||
областью дисперсии. Из (8.83) находим |
|
|
|||||
|
|
|
|
|
|
|
(8.84) |
|
|
|
|
|
|
|
|
Чем больше порядок дифракции , в котором анализируется |
|||||||
излучение, тем меньше допустимая область дисперсии. В частно- |
|||||||
сти, в первом порядке дифракции 1 может быть проанали- |
|||||||
зирован весь видимый диапазон излучения, однако разрешающая |
|||||||
способность при этом (8.80) минимальна. |
|
|
|||||
Интерферометр Фабри–Перо. Этот прибор, изобретенный |
|||||||
французскими |
физиками |
Ш. Фабри |
(1867–1945) и |
А. Перо |
|||
(1863–1925) представляет собой плоскопараллельную прозрач- |
|||||||
ную пластинку, на поверхность которой нанесены высокоотража- |
|||||||
ющие покрытия, либо интерферометр состоит из двух пластин |
|||||||
с параллельными отражающими покрытиями, разделенных воз- |
|||||||
душным промежутком. Многолучевая интерференция в данном |
|||||||
случае возникает за счет многократного переотражения пада- |
|||||||
ющей волны от высокоотражающих покрытий (зеркал) интер- |
|||||||
ферометра. Пусть плоская монохроматическая волна падает на |
|||||||
интерферометр под углом (угол между волновым вектором и |
|||||||
нормалью к отражающим поверхностям — осью на рис. 8.39). |
|||||||
Введем > |
и 3 — амплитудные коэффициенты пропускания и |
||||||
|
|
|
|
отражения зеркал. |
|
|
|
A0 |
L |
A1 |
|
Коэффициенты > и 3 связыва- |
|||
|
|
0 z |
ют между собой амплитуду падаю- |
||||
|
A2 |
щей на зеркало волны с амплитуда- |
|||||
|
|
rm |
|||||
|
|
|
ми прошедшей и отраженной волн. |
||||
|
n |
|
|
||||
|
A3 |
|
Согласно определению |
|
|||
|
|
|
|
||||
|
Рис. 8.39 |
|
прош пад >, |
отр пад 3 |
|||
Соответственно интенсивности волн связаны равенствами:
:прош :пад >2, :отр :пад 32. Будем полагать, что поглощение отсутствует. Тогда, очевидно :пад :прош :отр, откуда следует
>2 32 1. Если ввести энергетические коэффициенты отражения и пропускания и , то 1.
Пусть падающая на интерферометр волна имеет амплитуду0 (рис. 8.40). Пройдя внутрь интерферометра, волна ослабится, ее амплитуда станет равной 0>. Пройдя затем через второе зеркало, волна выйдет из интерферометра вправо, имея амплитуду1 0>2. Назовем эту волну первой волной.

8.10 ] |
|
|
Разрешающая способность спектральных приборов |
607 |
||||||
Однако часть волны (с амплитудой 0>) отразится от зер- |
||||||||||
кала |
2, а затем и |
от зеркала 1. После первого |
отражения |
|||||||
ее амплитуда станет равной 0>3, а после |
второго — 0>32. |
|||||||||
После |
выхода |
из |
интерферометра |
впра- |
|
|
|
|||
во (после прохождения сквозь зеркальное |
A0 |
A0 |
A1 |
|||||||
покрытие |
2), |
ее |
амплитуда |
станет |
рав- |
|
A0 |
|
||
ной |
2 |
0>32 > 0>232. Назовем эту |
|
A 2 |
A2 |
|||||
волну второй волной. Легко сообразить, |
|
0 |
|
|||||||
|
|
|
||||||||
что |
третья волна |
будет иметь амплитуду |
|
1 |
2 |
|||||
3 0>234. Итак, на выходе из интерферо- |
Рис. 8.40 |
метра мы имеем суперпозицию плоских волн, |
|
все они распространяются под углом к оси , а амплитуды этих волн отличаются множителем 32: 1 32.
Каждая последующая волна в этой суперпозиции проходит в интерферометре дополнительный путь 2+ (+ — расстояние между зеркалами), приобретая набег фазы #, равный 2+:
# 2+ |
(8.85) |
(для интерферометра, состоящего из двух зеркал, разделенных воздушным промежутком).
Таким образом, суммарная волна на выходе из интерферометра имеет амплитуду
|
|
2 232D' |
|
234D 2' |
2 |
|
||
|
|
|
0. |
(8.86) |
||||
|
> |
0 |
> |
0 |
> |
|
||
1 %2< |
||||||||
0 |
|
|
|
|
||||
(сумма бесконечной геометрической прогрессии со знаменателем 32D'). Амплитуда суммарной волны, прошедшей сквозь интерферометр, максимальна, если происходит синфазное сложение волн, т. е.
# 2+ 2$ ( — целое число) |
(8.87) |
При этом векторная диаграмма, изображающая сумму (8.86), представляет собой цепочку коллинеарных векторов, длины которых уменьшаются в геометрической прогрессии, а амплитуда прошедшей волны равна амплитуде падающей волны:
0 |
|
0, |
(8.88) |
|
1 |
||||
|
|
|
т. е. волна полностью проходит сквозь интерферометр! Поучительно рассчитать, какова при этом амплитуда отраженной волны (разумеется, мы должны получить в результате расчетаотр 0). Мы предоставляем проделать этот расчет читателю в качестве упражнения.
Синфазное сложение волн, возникающих при многократных переотражениях от зеркал (при условии (8.87)) приводит к тому, что амплитуда колебаний поля внутри резонатора может суще-